如果修改軟件不能實現(xiàn)所需速度，那么你可能順理成章的想到在你的設(shè)計中加入硬件加速模塊。

有很多種算法可對單精度浮點數(shù)字的正弦值進(jìn)行計算，但添加硬件加速器是功能最為強大的方法之一。之所以得出這一結(jié)論，是因為客戶的應(yīng)用要求使用此類正弦計算，而我們又針對能夠提供良好、快速且高效的解決方案進(jìn)行了多種方案的探索。

為了確定哪種實現(xiàn)方式最適合您的應(yīng)用，首先需要對代碼進(jìn)行分析，以查找哪種功能需要改進(jìn)；其次，由于修改軟件比修改硬件更簡便、迅速，因而請檢查是否能通過修改軟件來實現(xiàn)您所需的高速度（有時可以）。但是如果您還需要更高的性能，那么請考慮在硬件中實現(xiàn)部分算法。在硬件加速的支持下，您可以輕松勝過市場上任意微控制器或DSP。

為了解該流程，讓我們以現(xiàn)實案例為例，探討如何開發(fā)一個需要針對單精度浮點數(shù)字進(jìn)行正弦計算的軍事應(yīng)用。出于對高性價比的原因考慮，客戶已選擇了一款采用嵌入式 MicroBlaze?的Spartan?-6 FPGA 作為主系統(tǒng)控制器。可處理正弦計算的軟件算法應(yīng)運行于MicroBlaze 之上。

客戶的算法主要使用浮點運算。由于算法復(fù)雜，轉(zhuǎn)而采用定點運算并不妥當(dāng)。此外，客戶還希望避免使用定點運算時可能出現(xiàn)的運行過度或運行不足的情況。

客戶清楚 MicroBlaze IP 可提供兩種類型的浮點單元 (FPU)，并已選用擴展版本（相對于基本版而言）來加速算法。但是，這樣做就無法利用作為GNU工具鏈組成部分且隨 EDK 一起交付的數(shù)學(xué)仿真庫。數(shù)學(xué)庫中的軟件仿真例程程序運行速度非常慢，在任何情況下都應(yīng)盡量避免將其用于算法中對性能起到關(guān)鍵作用的部分。

另外，客戶還清楚 MicroBlaze FPU的兩個版本都只能處理單精度數(shù)據(jù)，不能處理雙精度數(shù)據(jù)。客戶的算法可以明確地僅使用浮點精度數(shù)據(jù) (float precision data)。但在開始使用數(shù)學(xué)函數(shù)時，有時也會進(jìn)行隱式轉(zhuǎn)換。這些轉(zhuǎn)換會強制算法
在不知不覺中使用雙精度數(shù)據(jù)。

步驟一：分析問題

我們的客戶已經(jīng)在運行他的算法，但發(fā)現(xiàn)該算法在MicroBlaze處理器上的運行速度偏慢。在對代碼庫進(jìn)行特性描述后，客戶發(fā)現(xiàn)引起速度慢的原因是正弦計算。下一步是找出其中原因并分析怎樣做才能加快處理速度。

第一種方案是使用數(shù)學(xué)庫提供的標(biāo)準(zhǔn)正弦函數(shù)，在客戶將算法寫入后，在不進(jìn)行任何修改的情況下完整地運行它。主要的問題在于數(shù)學(xué)庫函數(shù)僅針對雙精度數(shù)據(jù)而創(chuàng)建，這就意味著正弦函數(shù)的原型應(yīng)為如下所示：

double sin(double angle);

但客戶希望以下列方式使用：
float sin_val;
float angle;
...
sin_val = sin(angle);

當(dāng)然，這也是可能的，而且C編譯器會自動從參數(shù)角添加所需的轉(zhuǎn)換，進(jìn)行“雙精度化”，并將函數(shù)調(diào)用的結(jié)果轉(zhuǎn)回浮點值。這樣通常還是由數(shù)學(xué)庫函數(shù)來執(zhí)行兩個額外的轉(zhuǎn)換函數(shù)，甚至是正弦計算。

切記，MicroBlaze的FPU為單精度版本，只能完成如下執(zhí)行指令：

sin_val = (float)sin((double)angle);

由于數(shù)學(xué)庫的正弦函數(shù)是雙精度的，因而FPU無法完成正弦計算，故需要純軟件的解決方案。但缺點在于速度太慢，無法滿足客戶的需求。

我們驗證了使用雙精度數(shù)據(jù)進(jìn)行正弦值的計算是執(zhí)行緩慢的原因。首先我們使用下列代碼，從我們的執(zhí)行文件中直接創(chuàng)建匯編代碼：

mb-objdump.exe -D executable.elf
>dump.txt

檢查匯編代碼時，我們發(fā)現(xiàn)了如下代碼行：

brlid r15,-15832 // 4400d300

其作用是調(diào)用數(shù)學(xué)庫以進(jìn)行雙精度正弦計算。然后，我們測量了利用數(shù)學(xué)庫函數(shù)完成單次正弦計算所需的時間，約為 38,700個CPU周期。
對于特定的任務(wù)，可以使用專用單精度函數(shù)，如計算平方根：

float sqrt_f( float h);

使用專用函數(shù)可以避免單、雙精度函數(shù)之間的轉(zhuǎn)換，而且還可充分利用MicroBlaze FPU。

但遺憾的是，在FPU上沒有用于處理正弦計算的專用函數(shù)。此時，我們開始開發(fā)多個版本的算法來加速正弦值的計算，以實現(xiàn)更高的性能。

步驟二：創(chuàng)建更好的軟件算法

創(chuàng)建硬件加速器通常需要一段時間而且也需要進(jìn)行調(diào)試，因而我們試圖避免在第一次運行中就采取這種方案。我們就性能問題與客戶進(jìn)行了溝通，獲得了正弦計算的關(guān)鍵參數(shù)。

客戶的算法要求正弦計算的參數(shù)角應(yīng)具有1％的精度，而且計算出的正弦值精度應(yīng)比數(shù)學(xué)庫函數(shù)調(diào)用的結(jié)果高0.1%。
這些屬于關(guān)鍵參數(shù)，而且客戶告知我們，他有時必須按順序計算多個正弦值（比如在處理之前先填入小表格）。

由于對表格的尺寸要求， 使用填充了所有數(shù)值的查找表顯然不太可能。條目的最小數(shù)量為360,000個浮點數(shù)值（每個值 4 個字節(jié)）。客戶想找到高速解決方案，但在大小上也應(yīng)該合適。我們建議的解決方案可使用下列等式：

sin(xi) with xi = x + d

得到：

sin(x+d) = sin(x)*cos(d) +cos(x)*sin(d)

在這里，d是一個始終小于 x最小可能值（大于0）的值。這種解決方案有什么優(yōu)勢呢？我們需要縮小表格的大小，但會帶來計算量的增加。表格從開始就劃分為四個表格：

cos(x)
sin(x)
cos(d)
sin(d)

圖1和圖2顯示了所有4個表格所需的分辨率以及這些值通常情況下的表現(xiàn)。這些表格僅顯示了16個值的條目，用于說明需要填入我們的查找表中的值。我們在我們最終的解決方案中所使用的值要多得多。

?

?

圖 1 — x 值的正弦與余弦表，范圍介于0到360度之間

?

?

圖 2 — d 值的正弦與余弦表，范圍介于0到360/16度之間

實際上， 我們在每個表格中都使用了1 , 0 2 4 個值。X的最小值為360/1024=0.3515625 度。d 的所有值都將小于等于該值。該方法可以減少存儲的占用，因為完整的查找表需要 4,096個條目（每條目 4 個字節(jié)）。

使用這種方案，我們能夠?qū)崿F(xiàn)的自變量總體精度為：

360/(1024*1024) = 0,000343 degree

而且這個精度非常好。計算充分利用了MicroBlaze FPU。

真正的計算會占用一些時鐘周期，具體來說，需要進(jìn)行兩次fmul運算和一次fadd運算。不過，我們還需要進(jìn)行一些其它計算。首先，我們必須把自變量 xi拆分成兩個值，對應(yīng)x和d；然后，我們將這兩個值從表格中讀出；最后，我們必須使用新的算法才能計算結(jié)果。

我們在軟件中實現(xiàn)算法并對其進(jìn)行測試時，我們耗用的時鐘周期總數(shù)為6,520個。

為了進(jìn)一步提高分辨率，我們可以使用下列的象限關(guān)系：

第一象限

sin(x) = sin(x)

第二象限

sin(x) = sin(π - x)

第三象限

sin(x) = -sin(π + x)

第四象限：

sin(x) = -sin(2* π - x)

這在保持表格大小不變的同時還可將總體分辨率提高4倍。另一方面，我們需要進(jìn)行更多的計算才能找出我們必須進(jìn)行計算的象限是哪一個。仍然需要改進(jìn)算法或縮小表格的大小（縮小四分之幾）。我們還沒有進(jìn)行到這一步。

步驟三：優(yōu)化算法

由于我們的解決方案到目前為止，速度還不能滿足我們客戶的需要，因而我們需要稍做算法優(yōu)化，不過仍然完全采用運行在 MicroBlaze 處理器上的軟件。這是一種簡單的優(yōu)化方案，不過會降低部分精度。因此，我們創(chuàng)建了軟件模型（在PC上運行以提升運行速度）以運行所有可能的值，同時使用 sin()計算出的原始雙精度值與使用我們的軟件算法計算出的正弦值進(jìn)行比較。我們決定在標(biāo)準(zhǔn)的PC上運行算法，因為在MicroBlaze上進(jìn)行比較和計算需要花較長的時間（注意，我們的MicroBlaze運行速度遠(yuǎn)低于PC）。

現(xiàn)在我們開始優(yōu)化計算以獲得正弦值：

sin(x+d) = sin(x)*cos(d) +cos(x)*sin(d)

由于在每個表格中我們都使用了1,024個值，這意味著d始終小于360度／1,024個步進(jìn)，即：

cos(2* π /1024) = 0.99998

而且該值約等于1.0。對較小的d值，適用下列等式：

cos(d) = ~1.0

這樣可以將我們的公式簡化為如下等式：

sin(x+d) = sin(x) + cos(x)*sin(d)

在我們在MicroBlaze上實現(xiàn)新等式之前，我們使用PC模式對新等式的精度進(jìn)行了檢驗，發(fā)現(xiàn)最大誤差仍然低于我們客戶的目標(biāo)。

現(xiàn)在我們將該算法當(dāng)作軟件算法在MicroBlaze上實現(xiàn)，仍然使用每張帶有1,024個條目的表。新的算法只需要三個表，比之前的實現(xiàn)方案少一個。這樣既節(jié)省了存儲空間，也為更多的計算留出了時間。

我們在我們的硬件上測量了算法。一次正弦計算需要6,180個周期。

步驟四：進(jìn)一步優(yōu)化

另一種看似可行的優(yōu)化方式是轉(zhuǎn)換正弦計算的浮點值，并在此使用整數(shù)自變量。我們使用的算法使我們能夠創(chuàng)建~1E6 個不同的值 (1,024*1,024)。整數(shù)自變量足以處理這個數(shù)量的值。

這種優(yōu)化方式使我們能夠使用簡單得多的計算來將 xi 值拆分為 x 和 d。拆分只是一種簡單的“與”運算加上部分10 位的移位。我們參數(shù)角的上10位是xi，下10位是 d。

我們再次在PC上創(chuàng)建了一個軟件模型，并對其進(jìn)行檢驗，然后在MicroBlaze處理器系統(tǒng)上實現(xiàn)模型，這需要5,460個周期才能完成一次正弦計算。

步驟五：考慮硬件實現(xiàn)

雖然與數(shù)學(xué)庫的原始計算相比，算法的速度有了明顯的改善，但客戶需要的是速度快得多的實現(xiàn)。不過前文所述的最后一步給我們提供了一種能夠輕松轉(zhuǎn)向硬件實現(xiàn)的方法。

這種實現(xiàn)方法需要某些用于拆分 xi值的運算。要在硬件中做到這一點，只需將所需的位進(jìn)行連接即可。然后我們需要三個表；我們使用以我們的PC模型計算出的預(yù)定義值推導(dǎo)出ROM，然后將其轉(zhuǎn)入IP的VHDL代碼中。該IP能夠一次讀取所有三個表，從而能夠再度節(jié)省時間。最后，我們需要進(jìn)行一次浮點MUL和一次浮點ADD運算。

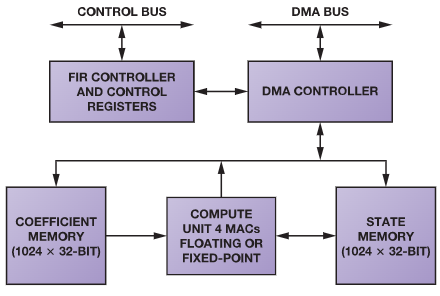
對于該任務(wù)，我們發(fā)現(xiàn)用于浮點運算的CORE GeneratorTM模塊非常適合。

?

?

圖 3 — 無流水線功能的加速器 IP

我們使用一些Slice和乘法器，對這些硬件模塊中的兩個進(jìn)行例化。兩個內(nèi)核都要求4到5個周期的延遲，以匹配我們設(shè)計的時序要求。延遲在此不是什么問題，我們將在下面的步驟中進(jìn)行討論。

我們將最終的IP以MicroBlaze的快速單工鏈路 (FSL) IP 的形式進(jìn)行實現(xiàn)。對時序的第一次估算結(jié)果表明：

? 將數(shù)據(jù)從MicroBlaze傳輸?shù)紽SL總線需用一個時鐘周期
? 將數(shù)據(jù)從FSL總線傳輸至FSL IP（當(dāng)正弦計算的自變量從FSL總線讀出時，將立即從BRAM讀取數(shù)據(jù)，因而無需時鐘周期）需用一個時鐘周期
? 完成MUL運算 (cos(x)*sin(d)) 需用四個時鐘周期
? 將方程的結(jié)果存儲到寄存器中需用一個時鐘周期
? 完成ADD運算需用四個時鐘周期
? 將數(shù)據(jù)發(fā)送回FSL總線需用一個時鐘周期
? MicroBlaze從FSL IP讀取數(shù)據(jù)需用一個時鐘周期。

請注意，在沒有使用任何額外流水線（我們將在下一步驟中討論這一點）的情況下，自變量數(shù)據(jù)在整個過程中必須保持穩(wěn)定。這就意味著MicroBlaze僅能請求一次正弦計算，且必須讀取該值，然后至少要等上13個時鐘周期，才能請求下一次計算。

因此，我們估計進(jìn)行該實現(xiàn)需要13個時鐘周期。當(dāng)然，要處理軟件上的函數(shù)調(diào)用以及某些其他運算，還需要更多的時鐘周期。

我們簡單地把一些標(biāo)準(zhǔn)時鐘組合在一起，不到一天就實現(xiàn)了該IP，隨即在硬件中對該算法進(jìn)行測量。整個算法（軟硬件混合）耗用了360個時鐘周期（包括所有的函數(shù)調(diào)用）。雖然這已是顯著的進(jìn)步，但是仍不足以充分滿足客戶的需求。

在我們的加速器IP處理所有數(shù)據(jù)之前，我們使用一個SRL16來延遲信號的寫入。

雖然該算法現(xiàn)在可與我們的MicroBlaze并行運行，但它每次只能計算一個值。

步驟六：添加流水線和適配客戶代碼

設(shè)計到了這一步，我們就可以開始向我們的內(nèi)核添加流水線。浮點ADD和浮點MUL的CORE Generator模塊已采用流水線實現(xiàn)，因而我們在此無需再做什么。第一個版本的算法要求自變量保持恒定，直至計算完成。在開始新計算之前（自變量數(shù)據(jù)到達(dá)FSL IP內(nèi)部），立刻讀取兩個BRAM并執(zhí)行浮點MUL。運算的結(jié)果在數(shù)個時鐘周期后生效。

我們的 sin(xi) 的自變量 xi 是一個20位寬的整數(shù)，它分為 x 和 d 兩個部分。因此，我們必須對自變量 xi的MSB部分 x 進(jìn)行幾個時鐘周期的延遲，以讀取 BRAM 的內(nèi)容，存儲自變量xi，并將其與MUL運算的結(jié)果相匹配。

我們?yōu)槲覀兊?0位寬數(shù)值使用了少量SRL16元件（總共 10 個），共占用了10個LUT（但由于Spartan-6具有LUT組合功能，如果采用該器件較寬的LUT6結(jié)構(gòu)，則僅需 5 個 LUT 即可）。

最后的工作量相當(dāng)小。在圖4中已對增加的SRL16x10位用紅圈進(jìn)行了標(biāo)注。

?

?

圖 4：帶流水線的加速器內(nèi)核

然后我們使用EDK向?qū)硇薷奈覀兊腇SL總線FIFO，以便存儲多個值（我們確定能夠存儲8個值就足以達(dá)到我們的目的，但可根據(jù)需要輕松增加更多）。

這就意味著我們的客戶甚至在請求第一個結(jié)果之前即能獲得多達(dá)8個值。這足以滿足我們客戶當(dāng)前的需求，但如果想請求更多正弦值的話，則可以輕松將FIFO緩沖參數(shù)擴展為較大的值。

我們在與客戶討論這種新的方案時，發(fā)現(xiàn)可將正弦計算進(jìn)一步劃分為兩個部分：

1. 請求正弦計算（fslput 運算）
2. 請求正弦計算的結(jié)果（fslget運算）

由于我們在運算中有一個固定時延，所以如果這兩個運算依次銜接、緊密地按順序執(zhí)行，那么MicroBlaze將停頓，并等待FSL IP完成對請求的處理。如果能夠?qū)⑦@兩組運算分開（這在客戶的算法中是可以的），那么我們即可進(jìn)一步提
升運算的總體速度。通過增加流水線， 在MicroBlaze上執(zhí)行的最終代碼如下：

putfsl(arg1,fsl1_id);
putfsl(arg2,fsl1_id);
putfsl(arg3,fsl1_id);
putfsl(arg4,fsl1_id);
putfsl(arg5,fsl1_id);
putfsl(arg6,fsl1_id);
putfsl(arg7,fsl1_id);
putfsl(arg8,fsl1_id);
...
getfsl(result1,fsl1_id);
getfsl(result2,fsl1_id);
getfsl(result3,fsl1_id);
getfsl(result4,fsl1_id);
getfsl(result5,fsl1_id);
getfsl(result6,fsl1_id);
getfsl(result7,fsl1_id);
getfsl(result8,fsl1_id);

這給我們帶來了顯著的優(yōu)勢。內(nèi)核不僅可完全實現(xiàn)流水線功能，而且還能夠?qū)⒄矣嬎愕膬蓚€調(diào)用分開。IP核的時延依然存在，但不再明顯。MicroBlaze也不再發(fā)生停頓和等待未完成的IP計算的情況，從而提高了整體性能。

客戶同意對代碼進(jìn)行相應(yīng)調(diào)整，這對客戶來說只是小量工作。通過使用C語言的宏命令取代函數(shù)調(diào)用，我們就能夠把所有要求的調(diào)用插入代碼庫中。

?

?

圖 5 － EDK為FSL總線實現(xiàn)了深度為 8 的 FIFO 以提升流水線的性能

最終實現(xiàn)的算法一次計算只需要四個時鐘周期。處理的總體時延不再明顯，而被調(diào)用的劃分以及結(jié)果請求所隱藏。另外，整體IP需要一些額外的BRAM（需為我們的三個表增加六個BRAM）和一定數(shù)量的乘法器或DSP Slice以及一些其他Slice。

但結(jié)果非常令人吃驚。我們的MicroBlaze現(xiàn)在就能夠如同超高端處理器內(nèi)核一樣運行，而且其運行頻率仍然相當(dāng)?shù)停ìF(xiàn)在比原來的正弦計算約快9,600 倍）。

步驟七：進(jìn)一步優(yōu)化？

當(dāng)我們達(dá)到這種實現(xiàn)水平時，我們的客戶對結(jié)果感到非常滿意，并且我們也完成了加速器IP方面的工作。速度和精度都非常不錯。

當(dāng)然，還有一項最終優(yōu)化需要完成。如果我們在d值非常小的情況下對sin(d) 值進(jìn)行考察，算法還可以進(jìn)一步完善：

sin(d) = ~d

若d值小于2*π/1024，即小于0.0061359，那么總體誤差則小于 1E-8（針對有 1,024 個值的表）。
我們算法的最后步驟將為：

sin(x+d) = sin(x) + cos(x) * d

這樣只會存在非常小的額外誤差，但我們可以去掉第三個表。當(dāng)然，我們必須保留 fadd 和 fmul運算器。雖然我們還可以通過其他方式來計算浮點值的正弦值，但這種方案充分顯示了增添硬件加速器的強大功能。我們的開發(fā)經(jīng)歷表明，你們無需為了將含有浮點計算的算法在硬件中實現(xiàn)而擔(dān)心。