學(xué)習(xí) tensorflow，caffe 等深度學(xué)習(xí)框架前，需要先了解一些基礎(chǔ)概念。本文以筆記的形式記錄了一個零基礎(chǔ)的小白需要先了解的一些基礎(chǔ)概念。

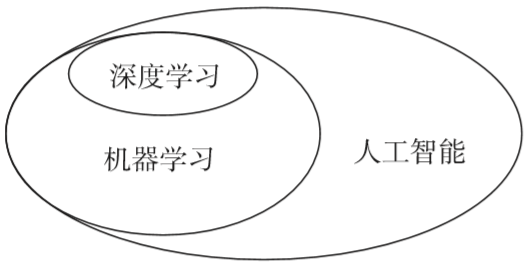
人工智能，機器學(xué)習(xí)和深度學(xué)習(xí)的關(guān)系

人工智能（Artificial Intelligence）——為機器賦予人的智能

"強人工智能"（General AI）：無所不能的機器，它有著我們所有的感知（甚至比人更多），我們所有的理性，可以像我們一樣思考

"弱人工智能"（Narrow AI）：弱人工智能是能夠與人一樣，甚至比人更好地執(zhí)行特定任務(wù)的技術(shù)。例如，Pinterest 上的圖像分類；或者 Facebook 的人臉識別。

強人工智能是愿景，弱人工智能是目前能實現(xiàn)的。

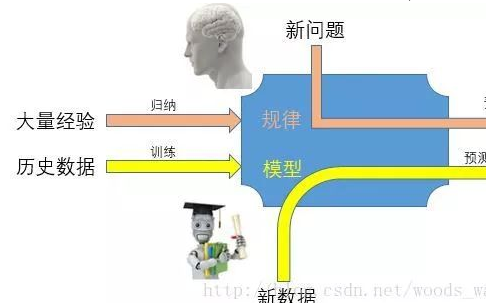
機器學(xué)習(xí)—— 一種實現(xiàn)人工智能的方法

機器學(xué)習(xí)最基本的做法，是使用算法來解析數(shù)據(jù)、從中學(xué)習(xí)，然后對真實世界中的事件做出決策和預(yù)測。

深度學(xué)習(xí)——一種實現(xiàn)機器學(xué)習(xí)的技術(shù)

機器學(xué)習(xí)可以通過神經(jīng)網(wǎng)絡(luò)來實現(xiàn)。可以將深度學(xué)習(xí)簡單理解為，就是使用深度架構(gòu)（比如深度神經(jīng)網(wǎng)絡(luò)）的機器學(xué)習(xí)方法。目前深度架構(gòu)大部分時候就是指深度神經(jīng)網(wǎng)絡(luò)。

神經(jīng)網(wǎng)絡(luò)組成

一個神經(jīng)網(wǎng)絡(luò)由許多神經(jīng)元組成，每個圓圈是一個神經(jīng)元，每條線表示神經(jīng)元之間的連接。x 表示的輸入數(shù)據(jù)，y 表示的是輸出數(shù)據(jù)，w 表示每層連接的權(quán)重。w 也就是我們構(gòu)造完神經(jīng)網(wǎng)絡(luò)之后需要確定的。

最左邊的叫做輸入層，這層負責(zé)接受輸入數(shù)據(jù)。

最右邊的叫做輸出層，我們可以從這層獲取神經(jīng)網(wǎng)絡(luò)輸出數(shù)據(jù)

輸入層和輸出層之間叫做隱藏層。隱藏層層數(shù)不定，簡單的神經(jīng)網(wǎng)絡(luò)可能是 2-3 層，復(fù)雜的也可能成百上千層，隱藏層較多的就叫做深度神經(jīng)網(wǎng)絡(luò)。

深層網(wǎng)絡(luò)比淺層網(wǎng)絡(luò)的表達能力更強，能夠處理更多的數(shù)據(jù)。但是深度網(wǎng)絡(luò)的訓(xùn)練更加復(fù)雜。需要大量的數(shù)據(jù)，很多的技巧才能訓(xùn)練好一個深層網(wǎng)絡(luò)。

問題：假設(shè)計算速度足夠快，是不是深度網(wǎng)絡(luò)越深越好？

不是。深度網(wǎng)絡(luò)越深，對架構(gòu)和算法的要求就越高。在超過架構(gòu)和算法的瓶頸后，再增加深度也是徒勞。

神經(jīng)元（感知器）

神經(jīng)網(wǎng)絡(luò)由一個個的神經(jīng)元構(gòu)成，而一個神經(jīng)元也由三部分組成。

輸入權(quán)值 每個輸入會對應(yīng)一個權(quán)值 w，同時還會有一個偏置值 b。也就是圖中的 w0。訓(xùn)練神經(jīng)網(wǎng)絡(luò)的過程，其實就是確定權(quán)值 w 的過程。

激活函數(shù) 經(jīng)過權(quán)值運算之后還會經(jīng)歷激活函數(shù)再輸出。比如我們可以用階躍函數(shù) f 來表示激活函數(shù)。

輸出 最終的輸出，感知器的輸出可以用這個公式來表示

神經(jīng)元可以擬合任意的線性函數(shù)，如最簡單擬合 and 函數(shù)。

and 函數(shù)真值表如上圖所示。取 w1 = 0.5；w2 = 0.5 b = -0.8。激活函數(shù)取上面示例的階躍函數(shù) f 表示。可以驗證此時神經(jīng)元能表示 and 函數(shù)。

如輸入第一行，x1 = 0，x2 = 0 時，可以得到

y 為 0，這就是真值表的第一行。

在數(shù)學(xué)意義上，可以這樣理解 and 函數(shù)的神經(jīng)元。它表示了一個線性分類問題，它就像是一條直線把分類 0（false，紅叉）和分類 1（true，綠點）分開

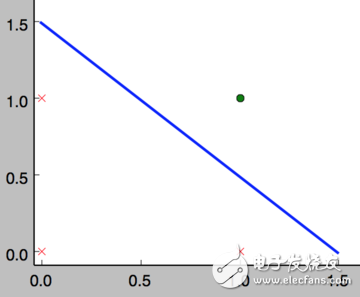
而實際上，神經(jīng)元在數(shù)學(xué)上可以理解為一個數(shù)據(jù)分割問題。神經(jīng)元是將神經(jīng)網(wǎng)絡(luò)轉(zhuǎn)換成數(shù)學(xué)問題的關(guān)鍵。比如需要訓(xùn)練神經(jīng)網(wǎng)絡(luò)做一個分類器，那么在數(shù)學(xué)上可以將輸入的參數(shù)（x1，x2...，xn）理解為 m 維坐標系（設(shè) x 是 m 元向量）上的 n 個點，而每個神經(jīng)元則可以理解為一個個擬合函數(shù)。取 m 為 2，放在最簡單的二維坐標系里面進行理解。

此時輸入?yún)?shù)對應(yīng)的是下圖中的黑點，每個神經(jīng)元就是黑線（由于激勵函數(shù)的存在，不一定像下圖一樣是線性的，它可以是任意的形狀）。神經(jīng)網(wǎng)絡(luò)由一個個神經(jīng)元組成，這些神經(jīng)元表示的擬合函數(shù)相互交錯就形成了各種各樣的區(qū)域。在下圖中可以直觀的看到，此時分類問題就是一個數(shù)學(xué)的問題，輸入?yún)?shù)落在 A 區(qū)域，那么就認為他是分類 1，落在 B 區(qū)域，則認為他是分類 2。依次類推，我們便建立了神經(jīng)網(wǎng)絡(luò)分類器在數(shù)學(xué)上的表現(xiàn)含義。

激活函數(shù)

事實上，一個神經(jīng)元不能擬合異或運算。在下圖中可以直觀的看到，你無法直接用一條直線將分類 0 和分類 1 分隔開。

此時可以借助激活函數(shù)來做分割。激活函數(shù)選擇閥值函數(shù)，也就是當輸入大于某個值時輸出 1（激活）,小于等于那個值則輸出 0（沒有激活）。

擬合異或函數(shù)的神經(jīng)網(wǎng)絡(luò)如圖所示：

圖中神經(jīng)網(wǎng)絡(luò)分成三層。在第二層中，如果輸入大于 1.5 則輸出 1，否則 0；第三層，如果輸入大于 0.5，則輸出 1，否則 0.

第一層到第二層（閥值 1.5）：

第二層到第三層（閥值 0.5）：

可以看到最終結(jié)果與異或結(jié)果吻合。

其實，這里放在數(shù)學(xué)上理解體現(xiàn)的是一個升維思想。放在二維坐標中無法分割的點，可以放在三維坐標中分割。上面的神經(jīng)網(wǎng)絡(luò)可以理解為只有最后一層，三個參數(shù)的神經(jīng)元。激活函數(shù)是用來構(gòu)造第三個參數(shù)的方式。這樣等同于將三個點放在三維坐標系中做數(shù)據(jù)分割。相當于在二維中無法解決中的問題升維到三維中解決。

深度學(xué)習(xí)過程

構(gòu)造神經(jīng)網(wǎng)絡(luò)

確定學(xué)習(xí)目標

學(xué)習(xí)

如何進行深度學(xué)習(xí)，過程基本都可以分為這三步來做。用一個簡單的例子來說明。如圖，假設(shè)我們需要通過深度學(xué)習(xí)來識別手寫圖片對應(yīng)的數(shù)字。

1.構(gòu)造神經(jīng)網(wǎng)絡(luò)。這里可以采用最簡單的全連接神經(jīng)網(wǎng)絡(luò)，也可以采用卷積神經(jīng)網(wǎng)絡(luò)。同時確定神經(jīng)元的激勵函數(shù)，神經(jīng)網(wǎng)絡(luò)的層數(shù)等。基礎(chǔ)概念篇不做過多介紹

2.確定學(xué)習(xí)目標。這里簡單假設(shè)我們所有輸入的都是手寫的數(shù)字圖片。那么這里就有 10 個輸出，分別對應(yīng) 0~9 的數(shù)字的比例。我們用 [y0,y1,...y9]表示，每個 y 值代表這張圖可能對應(yīng)該數(shù)字的概率（y0 表示這張圖是數(shù)字 0 的概率）。對于上圖中第一個輸入圖片，在訓(xùn)練過程中，我們知道第一張圖片輸出應(yīng)該是數(shù)字 5。于是我們期望輸出是 [0,0,0,0,0,1,0,0,0,0]。但是實際上，我們的模型不是完美的，肯定會有誤差，我們得到的結(jié)果可能是 [0,0,0.1,0,0,0.88,0,0,0,0.02]。那么就會有個訓(xùn)練得到的結(jié)果和期望結(jié)果的誤差。

這時候我們的學(xué)習(xí)目標也就是希望這個誤差能夠最小。誤差用 L 來表示，學(xué)習(xí)目標就是找到權(quán)值 w，使得 L 最小。當然，這里涉及到我們需要用一個公式來表達這個誤差 L，這個公式選取也很有學(xué)問，不同的公式最終在學(xué)習(xí)過程時收斂速度是不一樣的，通過訓(xùn)練模型得到的權(quán)值 w 也是不一樣的。這里先不多介紹。

3.學(xué)習(xí)。假設(shè)我們神經(jīng)模型確定下來的權(quán)值 w 與 L 的關(guān)系如圖所示（這里我們考慮最簡單的二維坐標下的情況，原理是相通的，推廣到多元坐標也是適用的）。由于數(shù)學(xué)模型的復(fù)雜，這里找最小值 L 的過程其實是找局部最小值的過程。

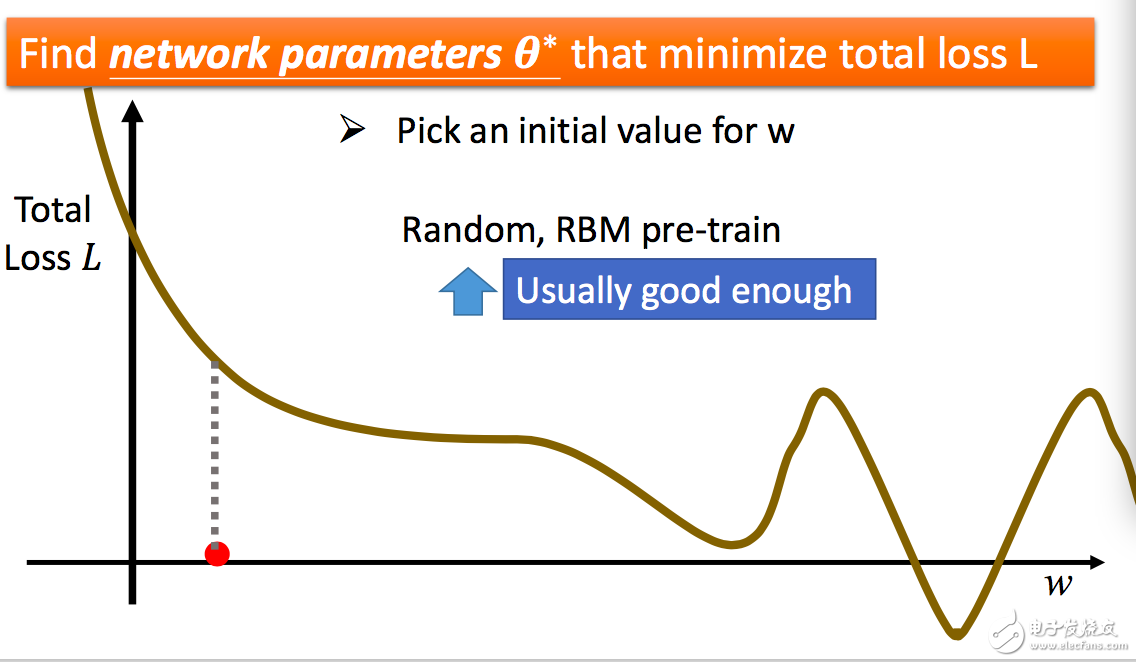
我們都知道，函數(shù)某個位置可導(dǎo)，那么就可以確定這個點的斜率。要找到局部最小值，可以根據(jù)這個點的斜率移動 w。如根據(jù)此時斜率的值我們可以確定 w 應(yīng)該向右移動一段距離。

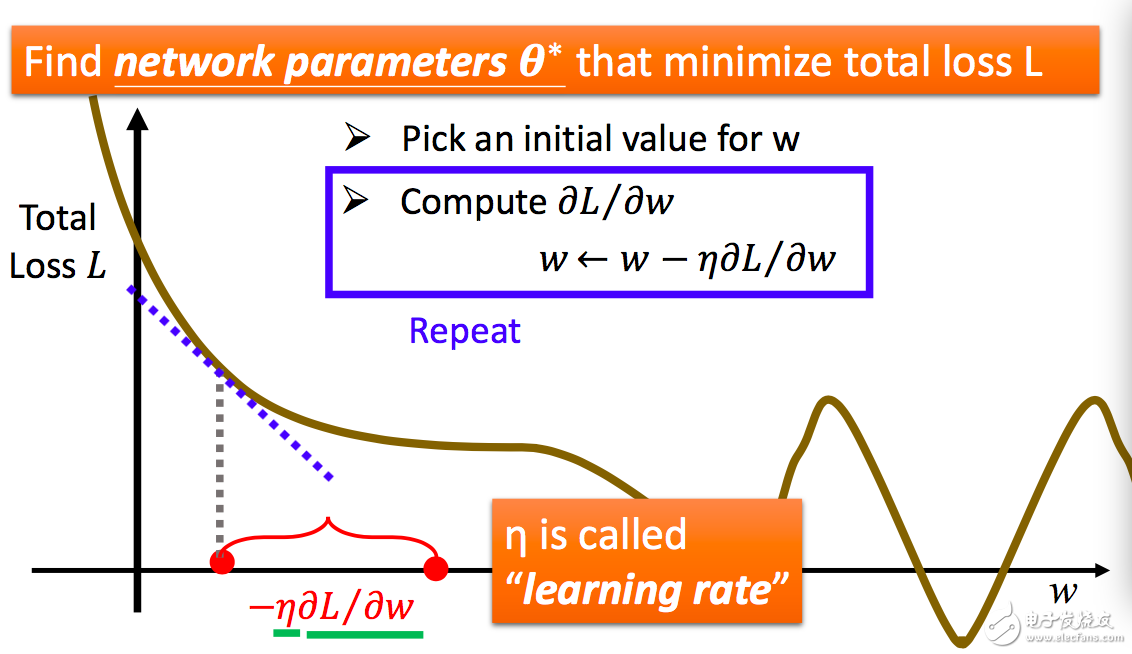
此時移動 w 的距離稱為步長。步長的選取很關(guān)鍵，如果步長過長，那么每次 w 偏移過大，永遠都找不到真正的最小值。而如果步長選取過小，那么收斂會變得很慢，而且有可能在中間某段平滑處停下來，找到的也不是真正的最小值。而步長怎么選擇呢？其實比較坑爹，某些時候有經(jīng)驗值，大部分時候則只能自己調(diào)整去試驗。

在學(xué)習(xí)的過程中，遇到的最常見的一個問題是"走不動"了。比如在下圖中。從 A 點走到 B 點，B 點由于斜率平滑，慢慢走到了 C 點，這時候可能 C 點斜率是平滑了，那么 w 將無法繼續(xù)往下走，永遠停留在 C 點！這樣得到的神經(jīng)網(wǎng)絡(luò)的誤差 L 顯然不是最小的，權(quán)值 w 也不是最佳的。

因此，在神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)過程中，常用的做法是模擬物理世界引入一個"動量球"。假設(shè)每次的移動看成 是一個"動量球"的移動。在移動過程中，"動量球"先從最高點往下走，雖然下載下來后斜率減少，但是由于"動量球"將移動下來的重力勢能轉(zhuǎn)變的動能，它會繼續(xù)往下走，從而移動過平緩區(qū)。當"動量球"到達某個局部最低點的時候，"動量球"會依靠自己的動能繼續(xù)滾動，設(shè)法尋找到下一個局部最低點。當然，"動量球"不是萬能的，它也可能會遇到"山坡"上不去最終滑下來停留在某個局部最小值（并不是真正的最小值）。但是"動量球"的引入，大大增加了學(xué)習(xí)過程的魯棒性，擴寬了局部最小值的尋找范圍。

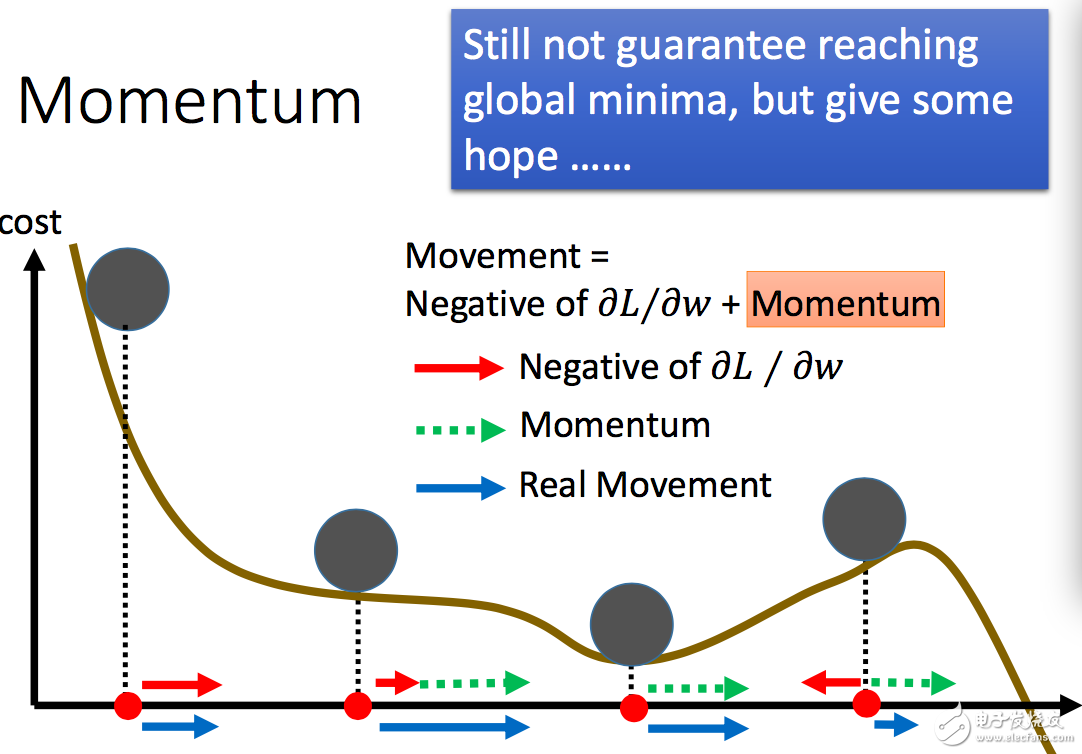
實際上，借助理解神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)的過程，我們會更加理解為什么深度越高的網(wǎng)絡(luò)不一定就越好。對于深度越高的神經(jīng)網(wǎng)絡(luò)，"平滑區(qū)"會越來越多，局部最小點也會越來越多。沒有合適的算法，很容易就陷入某個局部最小值里面去，而這個最小值可能還不如深度更淺的神經(jīng)網(wǎng)絡(luò)獲得的局部最小值小。也就是說，神經(jīng)網(wǎng)絡(luò)復(fù)雜之后，對架構(gòu)和算法的要求大大加高。

卷積

如果對卷積這個數(shù)學(xué)概念還沒有了解，可以先看知乎這里通俗的解釋。
怎樣通俗易懂地解釋卷積？

如果沒有做過圖像處理，還需要先看看卷積核，感受一下它的神奇。
圖像卷積與濾波的一些知識點

以圖片的卷積為例，深度學(xué)習(xí)中的卷積計算就是使用卷積核遍歷一張圖片的過程。

根據(jù)對于邊緣的處理不同，卷積分為相同填充和有效填充兩種方法。相同填充中，超出邊界的部分使用補充 0 的方法，使得輸入和輸出的圖像尺寸相同。而在有效填充中，則不使用補充 0 的方法，因此輸出的尺寸會比輸入尺寸小一些。

例 1：3*3 的卷積核在 5*5 的圖像上進行有效填充的卷積過程

例 2. 兩個 3*3*3 卷積核在 5*5 圖像上進行相同填充卷積過程。動圖

圖像有 r，g，b 三個通道。這里使用卷積核也分為 3 個通道分別進行卷積運算

池化

池化是卷積神經(jīng)網(wǎng)絡(luò)中用到的一種運算。在卷積神經(jīng)網(wǎng)絡(luò)中，卷積層后面一般是池化層。先進行卷積運算，再進行池化運算。

池化層在神經(jīng)網(wǎng)絡(luò)中起到的是降低參數(shù)和計算量，引入不變形的作用。

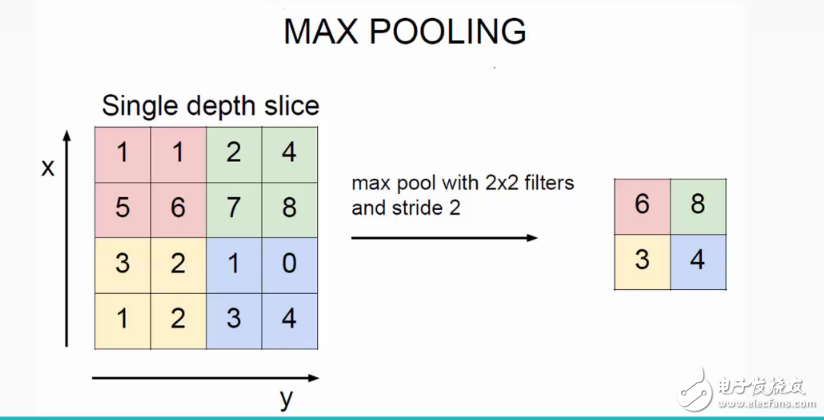
池化常用的是兩種，一種是 Avy Pooling，一種是 Max Pooling。下圖是 Max Pooling 的示意圖，可以看到分別找的是 2*2 矩陣中的最大值，Avy Pooling 則是將矩陣所有值加起來，求平均值。