基于位置的知識圖譜鏈接預測

人工智能技術與咨詢?

本文來自《中文信息學報》，作者張寧豫等

摘?要: 鏈接預測是知識圖譜的補全和分析的基礎。由于位置相關的實體和關系本身擁有豐富的位置特征，該文提出了一種基于位置的知識圖譜鏈接預測方法。該方法首先通過分析實體和關系的語義特征對關系進行分類，然后提出了一種基于位置的實體和關系位置特征和規則的挖掘方法；其次，通過挖掘出的實體位置特征和規則，對實體和關系的向量化方法預測結果進行約束，得到最終的結果。該文通過對WikiData、FB和WN數據集的實驗，證明該方法針對基于位置的關系和實體鏈接預測擁有較好的效果。

關鍵詞: 位置特征；知識圖譜；鏈接預測

0 引言

知識圖譜例如FreeBase、Yago等是很多人工智能應用的重要數據來源。它包含了海量的實體和關系并以三元組的形式進行存儲。然而，大多數知識庫的數據都是缺失的。所以知識庫補全，也就是對現有的知識庫進行鏈接，預測新的關系和實體是一項重要的工作。

現有的知識圖譜鏈接預測方法大多都是直接利用實體、關系本身或圖的特征來進行鏈接預測。對于給定的知識圖譜，實體和關系通常會被映射成低維的向量。通過定義一個打分函數來對每一對實體和關系的三元組進行預測。實體和關系的向量可以通過最大化已知正確三元組的打分函數來訓練獲得。

然而，在訓練實體、關系向量與打分函數的過程中，這類方法并沒有利用實體和關系本身隱藏的位置特征。此外,由于實體和關系向量化方法數據驅動特點，如果訓練結果中某一類關系或者實體數據量很小，訓練出的這一關系或實體的向量針對打分函數可能會導致過擬合等問題。

事實上，現有的知識庫中儲存著海量的位置相關的實體和關系。例如，在三元組(魯迅，WasBornIn，紹興)中，實體“紹興”有明確的位置特征。利用實體“紹興”的屬性可以獲得位置特征，進而可以推測實體“魯迅”隱含的位置特征，利用位置的隱含特征構造規則約束。例如，在判斷三元組(魯迅，WasBornIn， 浙江)是否成立時，利用實體“魯迅”的位置特征和空間位置的規則判斷，可以約束判斷的最終結果。

在本文中, 我們提出了一種針對位置關系的基于向量化和規則的鏈接預測方法。位置相關的關系指的是三元組中至少含有一個實體,其屬性或者本身含義帶有位置的特點。例如，至少有一個實體是一個地名、一個區域名稱、一個興趣點名稱等。

首先，針對基于位置的三元組，我們根據其特點把基于位置的關系分成了三類: 包含關系、相鄰關系和相交關系。包含關系是兩個實體本身的地理坐標范圍是相互包含的，例如LoactedIn。相鄰關系是指兩個實體本身的地理坐標范圍是相互分離的，但在一定距離內，例如NearBy。相交關系是指兩個實體本身的地理坐標范圍是相互交叉的，例如HasSameHometown。針對不同的實體，我們提取出不同的隱藏位置特征。針對不同的關系類型，我們提取不同的規則。實體的隱藏位置特征主要由實體本身的位置(如經緯度或地名)和它的輻射范圍組成。規則主要分成兩類: 一類是通用規則。例如，兩個實體間擁有NearBy 關系必然會存在HasNeighbour 關系，同時NearBy 關系的實體必須是屬于Location 類型的。另一類是位置規則。例如，實體h和實體t的隱藏位置特征是后者包含前者，則兩個實體間有可能存在包含這類的關系。最后，我們利用規則對向量化方法結果進行約束，得到最終的結果。

我們的方法有以下優點: (1)規則的使用降低了計算空間并提高了準確度；(2)保留了向量化方法的優點，同時加入了隱藏的位置信息；(3)它是一個通用的框架，能夠適用各種通用的向量化方法和規則。

綜上所述，本文的貢獻如下:

(1) 針對基于位置的三元組，我們提出了挖掘實體和關系位置特征的方法。

(2) 提出了一種針對位置關系的基于向量化和規則的鏈接預測方法。

(3) 利用WikiData、FB和WN的數據集進行實驗，證明針對位置相關的鏈接預測，本方法比其他方法準確度有所提高。

1 相關工作

知識圖譜的鏈接預測通常是指給定一組三元組，預測其成立的可能性。根據Nickel Maximilian[1]的研究，知識圖譜鏈接預測通常分為三大類: (1)通過實體和關系的隱含特征將其轉換成低維向量的方法[2-3]；(2)基于圖特征的方法[4-5]；(3) 基于馬爾科夫概率圖利用一階謂詞邏輯[6]或者軟邏輯(probabilistic soft logic)[7]來預測。

基于向量化的知識圖譜鏈接預測方法的核心是用向量來表達實體和關系隱藏的特征。RESCAL[2]和TransE[8]是兩個典型的方法。它們通過最小化結構風險或邊界誤差來學習隱藏的向量。然而，在學習和預測的過程中，這類方法都沒有利用潛在的位置特征和應用規則。

TRESCAL[9]將規則和RESCAL整合在了一起，但它僅能使用單一規則(例如某種關系的實體必須是特定的類型)。Rockt?schel等[10]提出了將一階謂詞邏輯映射成低維向量。但是他們的方法中規則并沒有直接起到鏈接預測的作用，也沒有降低預測的復雜度。

Wang Q等[11]提出了一種基于整數線性規劃(ILP)的方法，將向量化結果和規則整合起來進行鏈接預測，但是他們并沒有利用潛在的位置特征和基于位置的規則。基于圖的方法核心是挖掘知識圖譜圖結構所有的特征。Lü Lin[12]挖掘節點之間的相似度來進行鏈接預測。

Path ranking algorithm(PRA)[13]是利用節點之間不同通路包含的特征來進行預測，也可以提煉出規則來約束結果。但是，基于圖特征的方法通常適合局部的鏈接預測，不一定能挖掘出全局的隱藏特征。我們方法的不同點在于提供了一個通用的利用位置特征和規則的預測框架，可以整合各種向量化方法和規則。

在馬爾科夫網絡中，規則已經被大量使用，代表性的研究有利用一階謂詞邏輯[6]和軟邏輯(probabilistic soft logic)[7]。本文利用規則來約束向量化方法的結果，將整合問題變成一個整數規劃問題。此外，我們挖掘出了隱藏的位置特征，構造了位置特征的規則。

2 方法

2.1 定義

定義1(實體位置特征) 如果實體e能夠在當前知識庫或外部數據庫如Yago、GeoNames、 LinkedGeoData和WikiData中匹配到相應的位置(經緯度)和大致范圍或所屬上級的范圍，則e有位置特征fe=[lng,lat,D]，lng是經度，lat是緯度，D是一個描述實體包含范圍的數值，通常情況由實體本身的行政地域半徑或上級所屬區域半徑最小值確定。

定義2(位置相關三元組) 三元組(h,?r,?t)的實體h、t中至少有一個實體含有位置特征。

定義3(包含關系) 實體h和t的位置特征存在

?

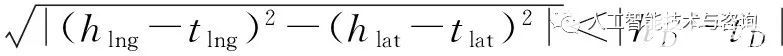
，則兩者存在包含關系HasContain(h,t)。

定義4(相鄰關系) 實體h?和t的位置特征存在

?

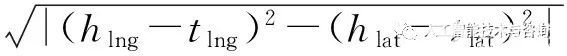
≥|hD+tD|，則兩者存在相鄰關系HasAdjacent(h,t)。

定義5(相交關系) 實體h和t的位置特征存在|hD-tD|≤

?

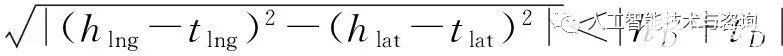
，則兩者存在相交關系HasIntersect(h,t)。

2.2 框架

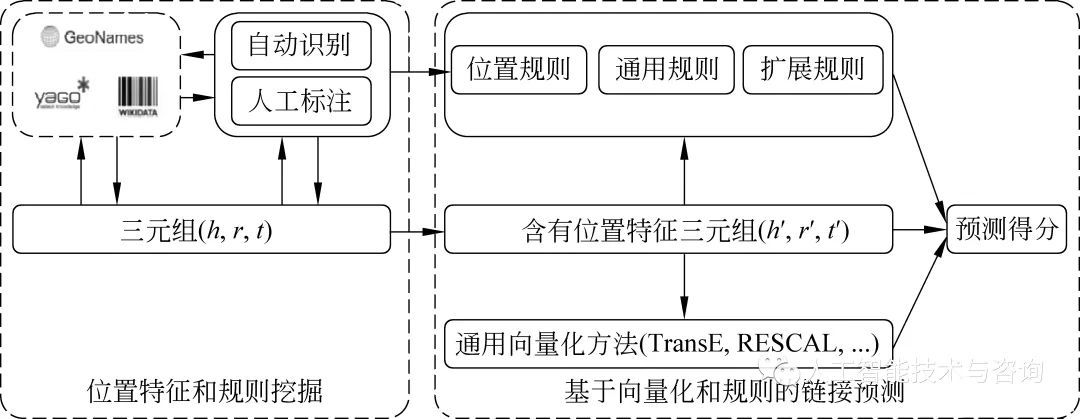
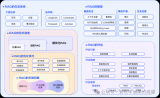
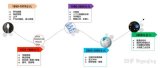
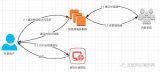
如圖2所示，我們的系統由兩部分組成：(1)位置特征和規則挖掘。首先對三元組中實體進行位置特征提取，然后對基于位置的三元組的關系進行自動識別或者人工標注分類，最后提取出其他可能存在的位置特征和規則。(2)基于向量化和規則的鏈接預測。首先對三元組利用向量化方法進行訓練，然后利用規則對結果進行約束。

?

圖2 框架系統的組成

2.3 隱含的位置特征和規則挖掘

給定一個基于位置的三元組(h,r,t), 首先我們需要提取出三元組中實體可以直接獲得的位置特征。例如，三元組(魯迅，WasBornIn, 紹興)中，通過對實體“魯迅”和“紹興”的類型和本地數據庫以及外部數據庫Yago、GeoName、LinkedGeoData和WikiData的匹配得到，實體“紹興”是一個地名。

我們可以獲得該實體的經緯度、面積、相鄰城市等信息。通過近似計算(利用面積或相鄰區域經緯度)，我們可以獲得實體“紹興”的位置特征。然后我們需要獲得關系“WasBornIn”的類別,即它屬于包含、相鄰、相交哪一類。一般地說，有兩種做法：(1)自動識別。

遍歷所有三元組中兩個實體都含有位置特征的三元組，通過反向計算實體位置特征的差異，推導出此三元組擁有的關系，對常見的如LocatedIn、Nearby等關系，此方法可以方便地判別；(2)人工標注。事實上，基于位置的關系總數并不多，再者，通常整個知識圖譜需要預測的關系數量級也不是很大，遠小于實體個數數量級。所以可以采取人工標注的方法來解決額外的關系分類問題。最后，我們通過已經獲得的關系“WasBornIn”屬于包含關系，判斷實體“魯迅”隱藏位置特征，該特征和實體“紹興”的位置特征存在包含關系。這個知識可以作為規則，為后續的未知鏈接預測做約束。

具體地說, 對于任意三元組(h,r,t), 如果只有實體t可以直接獲得位置特征ft=[tlng,tlat,tD]，根據關系r我們可以推測實體h隱含的位置特征。如果r屬于包含關系，則h可能`存在隱含位置特征[tlng,tlat,tD-μ]，其中0<μ

?

?

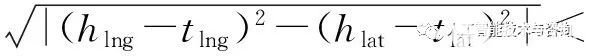
|hD+tD|，也就說是h位于一個環狀區域范圍內。如果r屬于相鄰關系，則h可能存在隱含位置特征 [hlng,hlat,hD]， 其中以上變量滿足條件

?

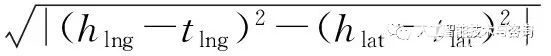
≥|hD+tD|。反之，如果實體h含有隱藏位置特征，以此來推導t，也是如此。事實上，對于相交和相鄰關系，大多數三元組的兩個實體本身都可以直接獲取位置關系。以上的隱藏特征都是近似特征。

由此，我們可以獲得海量的實體隱藏位置特征和規則。事實上，可以獲得以下規則:

規則1(實體類型匹配) 特定的關系擁有特定類型的實體。例如，關系LocatedIn擁有的兩個實體一定是Location 類型的；關系WasBornIn擁有的兩個實體一定是一個是Person類型，一個是Location類型。

規則2(參數個數匹配) 一對多和多對一的關系中特定實體的數目有一定限制。例如CityLocatedInCountry是一個多對一的關系。給定一個城市實體，在知識圖譜中最多存在一個國家實體與之對應。

規則3(相似關系匹配) 如果關系r1和r2存在一定的牽連或同屬于同一個類型(同是包含類型)，在不違背規則1、2的前提下，則擁有r1?關系的實體可能存在r2關系。例如, CityCapitalOfCountry->CityLocatedInCountry。

規則4(位置包含關系) 如果兩個實體的位置特征存在包含關系，則兩個實體可能存在包含關系。例如，實體“魯迅”和實體“浙江”的位置關系存在包含關系，則兩個實體很大程度上存在包含關系。

規則5(位置相鄰關系) 如果兩個實體的位置特征存在相鄰關系，則兩個實體可能存在相鄰關系。例如，實體“西湖”和實體“浙江大學”的位置關系存在相鄰關系，則兩個實體很大程度上存在相鄰關系。

規則6(位置相交關系) 如果兩個實體的位置特征存在相交關系，則兩個實體可能存在相交關系。例如，實體“金庸”和實體“徐志摩”的潛在的位置特征存在相交關系，則兩個實體可能存在相交關系。

規則7(位置包含傳導) 如果實體e2的位置特征包含實體e1的位置特征，實體e3的位置特征包含實體e2的位置特征，則實體e3和e1存在包含關系。包含關系可以一直連續傳遞，相鄰和相交關系不能傳遞。例如，實體“魯迅”和實體“浙江”存在包含關系，實體“浙江”和實體“中國”存在包含關系，則實體“魯迅”和實體“中國”存在包含關系。

此外，如果未知的一對一關系的三元組中，其中一個實體和關系存在于已知三元組正樣本中，那這個三元組很可能是不成立的。對于一些特殊的實體，可以通過幾重的關系鏈傳遞估計出位置特征的信息。例如，三元組(魯迅，說，中文)，實體“中文”的位置特征可以通過關系如“中國人說中文”、“中國人出生在中國”、“紹興位于浙江”、“浙江位于中國”和“紹興位于中國”等估計得到，其位置特征大致和實體“中國”的位置特征接近，從而估計出實體“中文”的位置特征。

2.4 基于向量化和規則的鏈接預測

給定一個知識圖譜，其包含n個實體，m個關系。我們可以獲得三元組集合O={h,r,t}。向量化方法的目的在于: (1)通過隱含的特征把實體和關系映射到一個向量；(2)利用訓練好的向量來預測新三元組成立的可能性。本文中我們利用了三種成熟的向量化方法: RESCAL、TRESCAL、 TransE。

RESCAL將每個實體ei當成一個向量ei∈Rd，每個關系rk都是一個矩陣Rk∈Rd×d。給定一個三元組(ei,rk,ej)，它的打分函數如式(1)所示。

f(ei,rk,

?

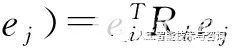
(1)

{e}和{rk}是通過最小化下面的結構損失函數來獲得的，如式(2)所示。

?

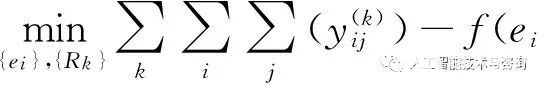
,rk,ej))2+λR

(2)

其中，如果三元組(ei,rk,ej)成立，則

?

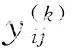
等于1，反之為0。R是正則項。λ是正則化參數，控制正則化和損失函數之間的平衡。

TRESCAL是RESCAL算法的一個擴展，需要對給定關系的實體類型進行約束。例如，給定關系rk和分別包含特定類型的實體集合Hk,Tk，則問題變成優化問題，如式(3)所示。

?

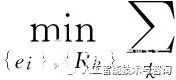
∑i∈

?

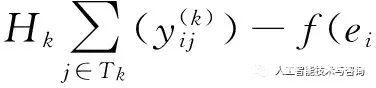
,rk,ej))2+λR

(3)

TransE將三元組(ei,rk,ej)映射成以下的三個向量ei,rk,ej∈Rd，它使用以下的打分函數來計算三元組成立的可能性，如式(4)所示。

f(ei,rk,ej)=||ei+rk-ej||

(4)

其中{ei}、{rk} 是通過優化式(5)的邊緣損失函數(正確樣本得到更高的得分，錯誤樣本得分更低)來得到:

?

γ-f(ei,rk,

?

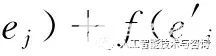
,rk,

?

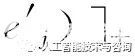
(5)

其中t+是正樣本，O是正樣本的集合，t-是負樣本，N是負樣本的集合。在替換過程中我們未采用隨機替換，而是替換之后確保新的三元組在原始的數據集中存在確定的關系，但關系不是rk, 這很大程度上確保了樣本是負樣本。我們利用隨機梯度下降的方法來求解優化問題。

利用上述方法，對未知的三元組，打分高的一般情況下成立的可能性較高，反之較低。我們將向量化方法得分的輸出記為

?

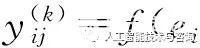
,rk,ej)，每個實體的位置特征記為fi、fj，標記相交關系集合Rintersect含三元組s?對，相鄰關系集合Radjacent含三元組p?對，包含關系集合Rcontain含三元組q?對，標記一對多、多對一、一對一關系集合R1-M,RM-1,R1-1, 標記特定關系所屬實體種類的集合Hk、Tk。用邏輯變量

?

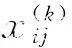
來標記這個三元組成立的最終可能。根據文獻[11]我們把規則約束向量化結果的問題定義為一個整數規劃的問題如式(6)所示①。

?

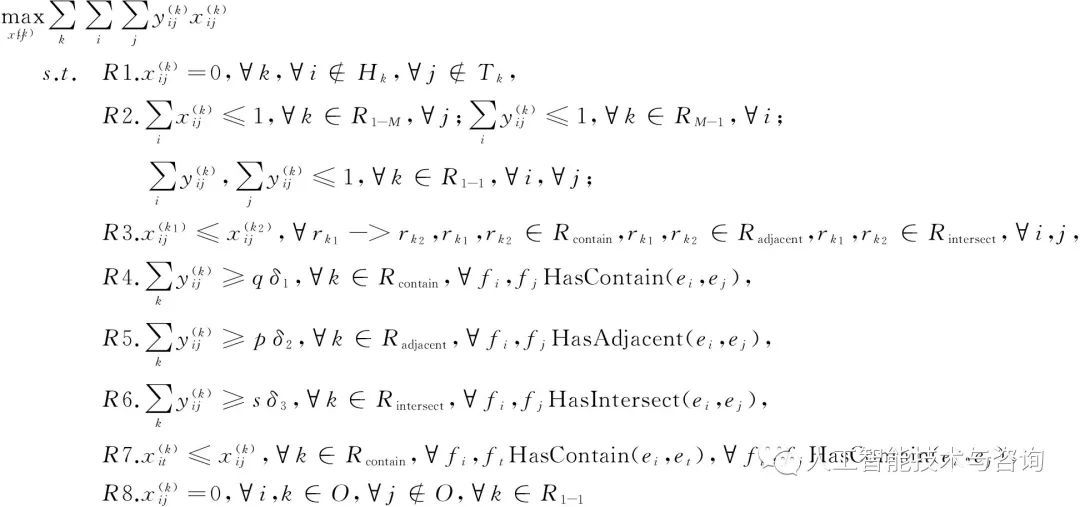
(6)

其中

?

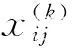
∈{0,1},?i,j,k，O是正樣本集合。通過解答上述問題求得最終的得分

?

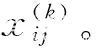
我們的方法優勢如下: (1) 在向量化方法的前提下，利用位置和通用規則，使含有顯性和隱性位置特征的三元組鏈接預測準確率有明顯的提高；(2)這是一個通用的框架，向量化方法和規則都可以靈活變化。

3 實驗

實驗的具體流程如下: (1)位置特征和規則挖掘；(2)基于向量化和規則的鏈接預測；(3)分析位置特征和規則對結果的影響。

3.1 數據集

在實驗中我們使用了三個數據集: WikiData-500K、WN-100K、FB-500K，分別從WikiData[14]、WordNet[15]、FreeBase[16]?獲取。WikiData是目前較大的一個開放的知識圖譜。WikiData包含有human、taxon、administrative territorial、architectural structure、event、chemical compound、film、thoroughfare、astronomical object等類型的實體組成的三元組信息。據我們統計有至少19.8%的三元組中至少有一個實體含有位置信息(事件、行政區劃、地點等)*,可以直接通過API獲取。我們由此構建了WikiData-500K數據集。WN-100K和FB-500K都是由不同學者發布出的三元組數據集。我們從WN-100K、FB-500K篩選出位置相關的三元組來進行訓練。具體地說，在完整知識庫中至少30%的三元組都滿足條件要求。此外，我們還利用Yago*、GeoNames*、LinkedGeoData*和WikiData對所有數據中的實體進行位置信息匹配，以獲得實體本身的位置特征。我們過濾了數據集中出現次數少于三次的實體，并采用了文獻[8]的方法來判斷實體的關系是一對多還是多對一來制定規則。此外，我們制定了一些同類匹配的規則。實驗數據集如表1所示。

?

3.2 特征和規則挖掘

我們的任務是提取出實體隱含的位置特征。首先，對數據集中所有的實體進行位置信息匹配。利用外部數據集擁有的準確地理位置信息匹配數據集中實體，大約40%的實體能匹配到準確的位置特征。然后，我們對數據集中擁有的關系進行分類。

利用自動分類方法標記了約63%的關系，剩下的關系采用人工標記。事實上，有約5%的關系是有歧義的，我們將它們默認歸到包含關系類。最后利用位置特征和關系類型挖掘剩下的實體隱藏位置特征。

3.3 鏈接預測

我們的任務是補全位置相關的三元組(h,r,t)，也就是說，給定h和t預測r或者給定h和r預測t，或者給定r和t預測h。本節中測試了RESCAL、TRESCAL、TransE，并把利用基于位置的規則來約束向量化結果的方法命名成l-RESCAL、l-TRESCAL、l-TransE。

對每個數據集，我們把基于位置的三元組按照4∶1的比例劃分成訓練集和測試集。對每一個實體我們都獲得其所屬類型。對于測試三元組，通過計算命中@10(正確命中結果排前十所占的比例)來衡量。在具體實驗中，RESCAL、TRESCAL的正則化參數λ=0.1，我們迭代訓練了十次。在向量化訓練過程中，我們將維度分別設置成10,20,50,100來選擇最優的參數。然后利用集成學習的方法獲得三種向量化方法的最優結果。在規則約束的過程中，δ1=0.7,δ2=0.6,δ3=0.4，我們使用lp solve*來解整數規劃問題。我們對規則約束重復進行了20 次取平均值，以獲得最優的結果。

表2展示了不同數據集下不同關系進行關系預測的結果。可以看出，利用基于位置的規則方法對特定的關系有顯著的提高。RESCAL和TRESCAL的提升幅度比TransE要高。

?

3.4 位置特征和規則分析

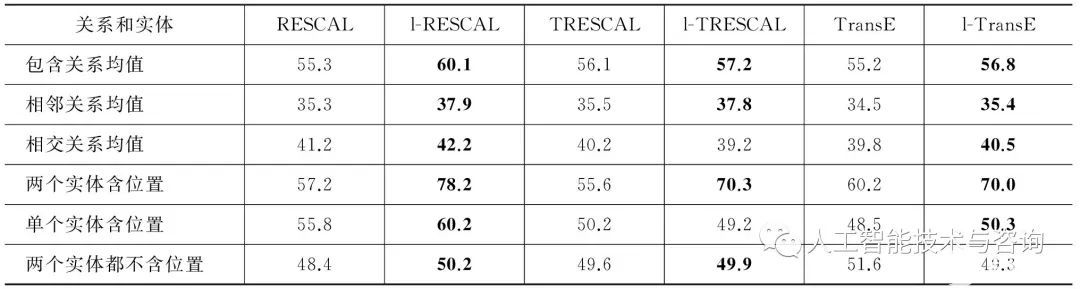
我們還對不同關系類型和不同實體進行了結果的比較，如表3所示。從結果可以看出，對我們的方法，包含關系獲得的提升程度 較 高，其 次 是 相鄰關系和相交關系。事實上，包含關系的位置隱含特征區域較為狹小，因此對關系的確定限制較大，可以獲得較好的結果；而相鄰關系和相交關系(實體都可以直接獲得位置特征除外)獲取的隱藏位置區域較大，因此限制較為不準確。對實體而言，兩個實體都可以直接獲得位置關系的預測結果提升幅度最大，其次是單一實體的結果。有趣的是，對于兩個都不能直接獲得位置信息的實體，本方法仍能獲得少量的提升。事實上，例如判斷三元組(徐志摩，HasSameHometown，金庸)時，實體“徐志摩”和“金庸”的隱藏位置特征是可以獲得的, 利用人工標記關系“HasSameHometown”為相交關系，使用我們的方法可以獲得準確度的提升。

表3?不同類型關系命中@10結果/%

?

4 結論

本文提出了一種針對位置關系的基于向量化和規則的鏈接預測方法。實體位置特征和規則的使用降低了計算空間，提高了基于位置鏈接預測的準確度。我們還對位置特征和規則進行了實驗分析。

實驗結果證明，對于特定類型的關系，位置特征和規則的利用可以使鏈接預測的準確度得到一定程度的提高。將來，我們計劃：(1)分布式我們的方法，使得它能夠適用于更大的數據集；(2)加入更加復雜的空間規則；(3)嘗試在向量化訓練的同時直接利用規則，以提高準確度。

審核編輯：金巧

?

?