秘笈三 阻尼輸入濾波系列第一部分

　　開關調節器通常優于線性調節器，因為它們更高效，而開關拓撲結構則十分依賴輸入濾波器。 這種電路元件與電源的典型負動態阻抗相結合， 可以誘發振蕩問題。本文將闡述如何避免此類問題的出現。

　　一般而言，所有的電源都在一個給定輸入范圍保持其效率。因此，輸入功率或多或少地與輸入電壓水平保持恒定。 圖3.1顯示的是一個開關電源的特征。 隨著電壓的下降，電流不斷上升。

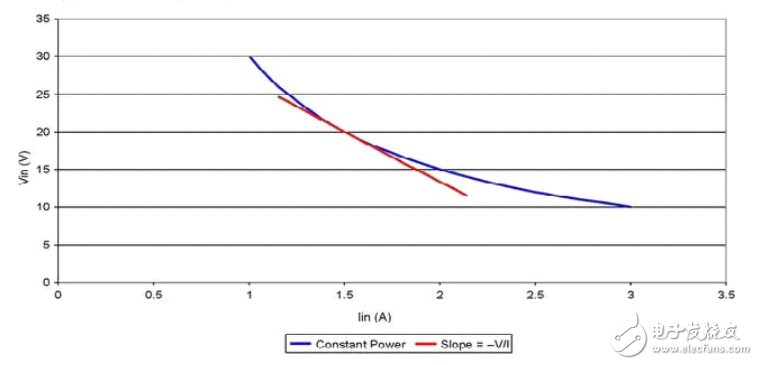
　　圖3.1 開關電源表現出的負阻抗

　　負輸入阻抗

　　電壓-電流線呈現出一定的斜率， 其從本質上定義了電源的動態阻抗。 這根線的斜率等于負輸入電壓除以輸入電流。 也就是說， 由Pin=V?， 可以得出V=Pin/I； 并由此可得dV/dI=–Pin/I2或dV/dI≈–V/I。

　　該近似值有些過于簡單，因為控制環路影響了輸入阻抗的頻率響應。但是很多時候，當涉及電流模式控制時這種簡單近似值就已足夠了。

　　為什么需要輸入濾波器

　　開關調節器輸入電流為非連續電流，并且在輸入電流得不到濾波的情況下其會中斷系統的運行。 大多數電源系統都集成了一個如圖3.2所示類型的濾波器。 電容為功率級的開關電流提供了一個低阻抗，而電感則為電容上的紋波電壓提供了一個高阻抗。該濾波器的高阻抗使流入源極的開關電流最小化。在低頻率時，該濾波器的源極阻抗等于電感阻抗。在您升高頻率的同時，電感阻抗也隨之增加。在極高頻率時，輸出電容分流阻抗。在中間頻率時，電感和電容實質上就形成了一種并聯諧振電路，從而使電源阻抗變高，呈現出較高的電阻。

　　大多數情況下，峰值電源阻抗可以通過首先確定濾波器 （Zo） 的特性阻抗來估算得出，而濾波器特性阻抗等于電感除以電容所得值的平方根。這就是諧振下電感或者電容的阻抗。 接下來， 對電容的等效串聯電阻 （ESR） 和電感的電阻求和。 這樣便得到電路的Q值。峰值電源阻抗大約等于Zo乘以電路的Q值。

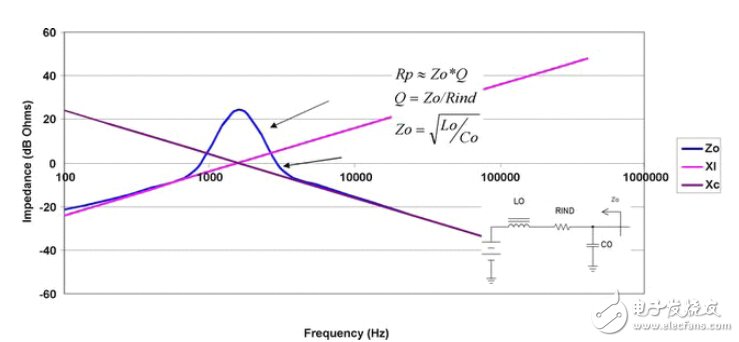
　　圖3.2 諧振時濾波器的高阻抗和高阻性

　　振蕩

　　但是， 開關的諧振濾波器與電源負阻抗耦合后會出現問題。 圖3.3顯示的是在一個電壓驅動串聯電路中值相等、極性相反的兩個電阻。這種情況下，輸出電壓趨向于無窮大。當您獲得由諧振輸入濾波器等效電阻所提供電源的負電阻時，您也就會面臨一個類似的電源系統情況；這時，電路往往就會出現振蕩。

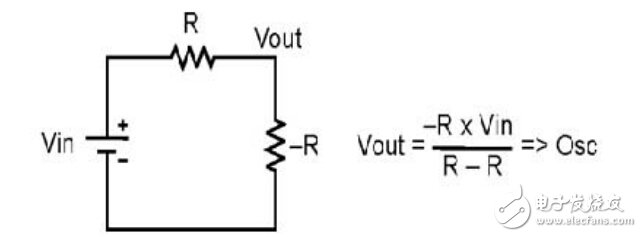
　　圖3.3 與其負阻抗耦合的開關諧振濾波器可引起不必要的振蕩

　　設計穩定電源系統的秘訣是保證系統電源阻抗始終大大小于電源的輸入阻抗。我們需要在最小輸入電壓和最大負載（即最低輸入阻抗）狀態下達到這一目標。

　　秘笈四 阻尼輸入濾波系列第二部分

　　控制源極阻抗

　　在“電源設計秘笈3”中， 我們討論了輸入濾波器的源極阻抗如何變得具有電阻性，以及其如何同開關調節器的負輸入阻抗相互作用。在極端情況下，這些阻抗振幅可以相等，但是其符號相反從而構成了一個振蕩器。業界通用的標準是輸入濾波器的源極阻抗應至少比開關調節器的輸入阻抗低6dB， 作為最小化振蕩概率的安全裕度。

　　輸入濾波器設計通常以根據紋波電流額定值或保持要求選擇輸入電容（圖4.1所示CO）開始的。第二步通常包括根據系統的EMI要求選擇電感 （LO）。正如我們上個月討論的那樣，在諧振附近，這兩個組件的源極阻抗會非常高，從而導致系統不穩定。 圖 1 描述了一種控制這種阻抗的方法， 其將串聯電阻 （RD） 和電容 （CD） 與輸入濾波器并聯放置。利用一個跨接 CO 的電阻，可以阻尼濾波器。但是，在大多數情況下，這樣做會導致功率損耗過高。另一種方法是在濾波器電感的兩端添加一個串聯連接的電感和電阻。

　　圖4.1 CD和RD阻尼輸出濾波器源極阻抗

　　選擇阻尼電阻

　　有趣的是，一旦選擇了四個其他電路組件，那么就會有一個阻尼電阻的最佳選擇。圖4.2 顯示的是不同阻尼電阻情況下這類濾波器的輸出阻抗。紅色曲線表示過大的阻尼電阻。請思考一下極端的情況，如果阻尼電阻器開啟，那么峰值可能會非常的高，且僅由CO和LO來設定。藍色曲線表示阻尼電阻過低。如果電阻被短路，則諧振可由兩個電容和電感的并聯組合共同設置。綠色曲線代表最佳阻尼值。利用一些包含閉型解的計算方法（見參考文獻 1）就可以很輕松地得到該值。

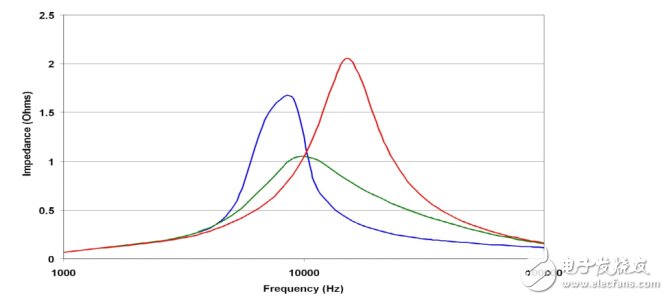
　　圖4.2 在給定CD-CO比的情況下，有一個最佳阻尼電阻

　　選擇組件

　　在選擇阻尼組件時，圖4.3非常有用。該圖是通過使用RD Middlebrook建立的閉型解得到的。橫坐標為阻尼濾波器輸出阻抗與未阻尼濾波器典型阻抗 （ZO=（LO/CO）1/2） 的比。 縱坐標值有兩個： 阻尼電容與濾波器電容 （N） 的比； 以及阻尼

　　電阻同該典型阻抗的比。 利用該圖， 首先根據電路要求來選擇LO和CO， 從而得到ZO。

　　隨后，將最小電源輸入阻抗除以二，得到您的最大輸入濾波器源極阻抗 （6dB）。最小電源輸入阻抗等于Vinmin2/Pmax。只需讀取阻尼電容與濾波器電容的比以及阻尼電阻與典型阻抗的比， 您便可以計算得到一個橫坐標值。例如，一個具有10μH電感和10μH 電容的濾波器具有Zo= （10μH/10μF）1/2=1Ohm 的典型阻抗。 如果它 正對 一個 12V 最 小輸 入的 12W 電 源進 行濾 波， 那么 該電 源輸 入阻 抗將 為Z=V2/P=122/12=12Ohms。這樣，最大源極阻抗應等于該值的二分之一，也即6Ohms。

　　現在，在6/1=6的X軸上輸入該圖，那么，CD/CO=0.1，即1μF，同時RD/ZO=3，也即3Ohms。

　　圖4.3 選取LO和CO后，便可從最大允許源極阻抗范圍內選擇CD和RD

　　秘笈五 降壓—升壓電源設計中降壓控制器的使用

　　電子電路通常都工作在正穩壓輸出電壓下，而這些電壓一般都是由降壓穩壓器來提供的。如果同時還需要負輸出電壓，那么在降壓—升壓拓撲中就可以配置相同的降壓控制器。負輸出電壓降壓—升壓有時稱之為負反向，其工作占空比為50%， 可提供相當于輸入電壓但極性相反的輸出電壓。其可以隨著輸入電壓的波動調節占空比，以“降壓”或“升壓”輸出電壓來維持穩壓。

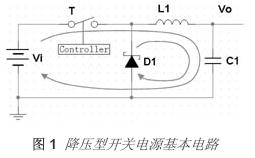
　　圖 5.1顯示了一款精簡型降壓—升壓電路，以及電感上出現的開關電壓。這樣一來該電路與標準降壓轉換器的相似性就會頓時明朗起來。實際上，除了輸出電壓和接地相反以外，它和降壓轉換器完全一樣。這種布局也可用于同步降壓轉換器。這就是與降壓或同步降壓轉換器端相類似的地方，因為該電路的運行與降壓轉換器不同。

　　FET開關時出現在電感上的電壓不同于降壓轉換器的電壓。 正如在降壓轉換器中一樣， 平衡伏特-微秒 （V-μs） 乘積以防止電感飽和是非常必要的。 當FET為開啟時（如圖 1 所示的ton間隔），全部輸入電壓被施加至電感。這種電感“點”側上的正電壓會引起電流斜坡上升， 這就帶來電感的開啟時間V-μs乘積。 FET 關閉 （toff）期間，電感的電壓極性必須倒轉以維持電流，從而拉動點側為負極。電感電流斜坡下降， 并流經負載和輸出電容， 再經二極管返回。 電感關閉時V-μs乘積必須等于開啟時V-μs乘積。由于Vin和Vout不變，因此很容易便可得出占空比 （D） 的表達式：

　　D=Vout/（Vout “ Vin）。 這種控制電路通過計算出正確的占空比來維持輸出電壓穩壓。

　　上述表達式和圖5.1所示波形均假設運行在連續導電模式下。

　　圖 5.1 降壓—升壓電感要求平衡其伏特-微秒乘積

　　降壓 — 升壓電感必須工作在比輸出負載電流更高的電流下。其被定義為IL=I《SUBOUT《 sub》/（1-D），或只是輸入電流與輸出電流相加。對于和輸入電壓大小相等的負輸出電壓（D =0.5）而言，平均電感電流為輸出的2倍。

　　有趣的是，連接輸入電容返回端的方法有兩種，其會影響輸出電容的rms電流。典型的電容布局是在 +Vin 和 Gnd 之間，與之相反，輸入電容可以連接在 +Vin 和”V《SUBOUT《 sub》 之間。利用這種輸入電容配置可降低輸出電容的rms電流。然而，由于輸入電容連接至 “Vout，因此 ”Vout上便形成了一個電容性分壓器。這就在控制器開始起作用以前， 在開啟時間的輸出上形成一個正峰值。 為了最小化這種影響，最佳的方法通常是使用一個比輸出電容要小得多的輸入電容， 請參見圖5.2所示的電路。輸入電容的電流在提供dc輸出電流和吸收平均輸入電流之間相互交替。rms 電流電平在最高輸入電流的低輸入電壓時最差。因此，選擇電容器時要多加注意，不要讓其ESR過高。陶瓷或聚合物電容器通常是這種拓撲較為合適的選擇。

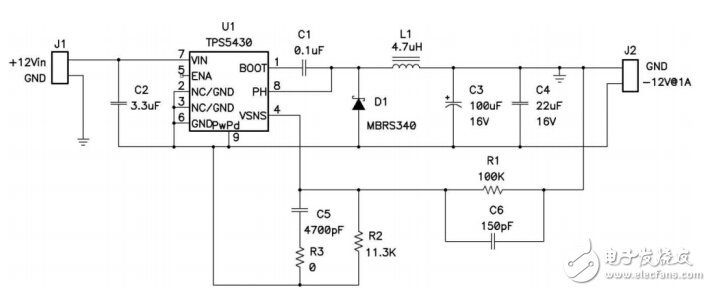
　　圖5.2 降壓控制器在降壓—升壓中的雙重作用

　　必須要選擇一個能夠以最小輸入電壓減去二極管壓降上電的控制器，而且在運行期間還必須能夠承受得住Vin加Vout的電壓。FET和二極管還必須具有適用于這一電壓范圍的額定值。通過連接輸出接地的反饋電阻器可實現對輸出電壓的調節，這是由于控制器以負輸出電壓為參考電壓。只需精心選取少量組件的值，并稍稍改動電路，降壓控制器便可在負輸出降壓—升壓拓撲中起到雙重作用。