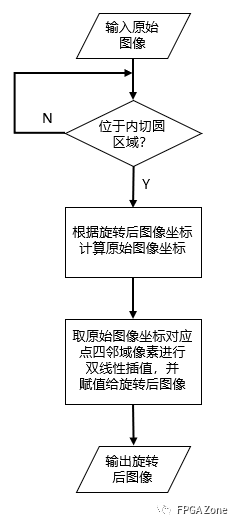
旋轉一般是指將圖像圍繞某一指定點旋轉一定的角度，圖像旋轉后會有一部分圖像轉出顯示區域，可以截圖那部分，也可以改變圖像的尺寸使得圖像顯示完全。

　　圖像旋轉原理

　　所謂圖像旋轉是指圖像以某一點為中心旋轉一定的角度，形成一幅新的圖像的過程。這個點通常就是圖像的中心。

　　由于是按照中心旋轉，所以有這樣一個屬性：旋轉前和旋轉后的點離中心的位置不變。

　　根據這個屬性，可以得到旋轉后的點的坐標與原坐標的對應關系。

　　原圖像的坐標一般是以左上角為原點的，我們先把坐標轉換為以圖像中心為原點。假設原圖像的寬為w，高為h，（x0，y0）為原坐標內的一點，轉換坐標后的點為（x1，y1）。可以得到：

　　X0’ = x0 -w/2;

　　y1’ =-y0 + h/2;

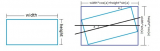
　　在新的坐標系下，假設點（x0，y0）距離原點的距離為r，點與原點之間的連線與x軸的夾角為b，旋轉的角度為a，旋轉后的點為（x1，y1）， 如下圖所示。

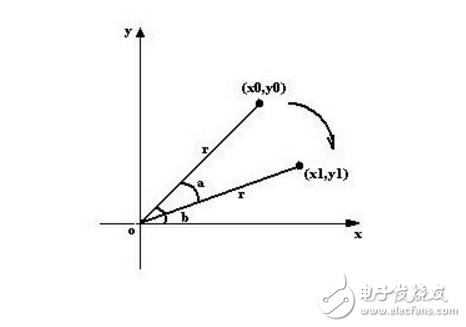
　　那么有以下結論：

　　x0=r*cosb；y0=r*sinb

　　x1 = r*cos（b-a）= r*cosb*cosa+r*sinb*sina=x0*cosa+y0*sina；

　　y1=r*sin（b-a）=r*sinb*cosa-r*cosb*sina=-x0*sina+y0*cosa；

　　得到了轉換后的坐標，我們只需要把這些坐標再轉換為原坐標系即可。

　　x1’ = x1+w/2= x0*cosa+y0*sina+w/2

　　y1’=-y1+h/2=-（-x0*sina+y0*cosa）+h/2=x0*sina-y0*cosa+h/2

　　此處的x0/y0是新的坐標系中的值，轉換為原坐標系為：

　　x1’ = x0*cosa+y0*sina+w/2=（x00-w/2）*consa+（-y00+h/2）*sina+w/2

　　y1’= x0*sina-y0*cosa+h/2=（x00-w/2）*sina-（-y00+h/2）*cosa+h/2

　　=（y00-h/2）*cosa+（ x00-w/2）*sina+h/2

　　在OpenCV中，目前并沒有現成的函數直接用來實現圖像旋轉，它是用仿射變換函數cv：：warpAffine來實現的，此函數目前支持4種插值算法，最近鄰、雙線性、雙三次、蘭索斯插值，如果傳進去的參數為基于像素區域關系插值算法（INTER_AREA），則按雙線性插值。

　　通常使用2*3矩陣來表示仿射變換：

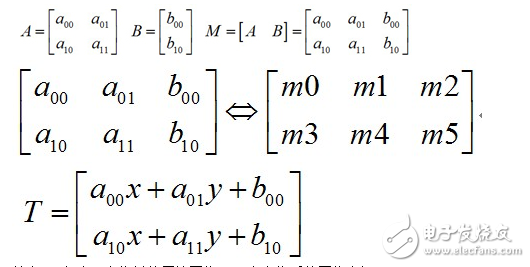
　　其中，T相當于變換前的原始圖像，x，y為變換后的圖像坐標。

　　對于cv：：getRotationMatrix2D函數的實現公式為：

　　其中scale為縮放因子（x、y方向保持一致），angle為旋轉角度（弧長），centerx，centery為旋轉中心。

　　1 旋轉矩形

　　這里以圖像圍繞任意點（center_x， center_y）旋轉為例，但是圖像的原點在左上角，在計算的時候首先需要將左上角的原點移到圖像中心，并且Y軸需要翻轉。

　　而在旋轉的過程一般使用旋轉中心為坐標原點的笛卡爾坐標系，所以圖像旋轉的第一步就是坐標系的變換。（x’，y’）是笛卡爾坐標系的坐標，（x，y）是圖像坐標系的坐標，經過坐標系變換后

　　坐標系變換到以旋轉中心為原點后，接下來就要對圖像的坐標進行變換。

　　逆變換是

　　由于在旋轉的時候是以旋轉中心為坐標原點的，旋轉結束后還需要將坐標原點移到圖像左上角，也就是還要進行一次變換。

　　上邊兩圖，可以清晰的看到，旋轉前后圖像的左上角，也就是坐標原點發生了變換。

　　在求圖像旋轉后左上角的坐標前，先來看看旋轉后圖像的寬和高。從上圖可以看出，旋轉后圖像的寬和高與原圖像的四個角旋轉后的位置有關。

　　我們將這個四個角點記為 transLeftTop， transRightTop， transLeftBottom， transRightBottom

　　設top為旋轉后最高點的縱坐標 top = min（{ transLeftTop.y， transRightTop.y， transLeftBottom.y， transRightBottom.y }）;

　　down為旋轉后最低點的縱坐標 down = max（{ transLeftTop.y， transRightTop.y， transLeftBottom.y， transRightBottom.y }）;

　　left為旋轉后最左邊點的橫坐標 left = min（{ transLeftTop.x， transRightTop.x， transLeftBottom.x， transRightBottom.x }）;

　　right為旋轉后最右邊點的橫坐標 right = max（{ transLeftTop.x， transRightTop.x， transLeftBottom.x， transRightBottom.x }）;

　　旋轉后的寬和高為newWidth，newHeight，則可得到下面的關系：

　　旋轉完成后要將坐標系轉換為以圖像的左上角為坐標原點，可由下面變換關系得到：

　　逆變換

　　綜合以上，也就是說原圖像的像素坐標要經過三次的坐標變換：

　　將坐標原點由圖像的左上角變換到旋轉中心

　　以旋轉中心為原點，圖像旋轉角度a

　　旋轉結束后，將坐標原點變換到旋轉后圖像的左上角

　　可以得到下面的旋轉公式：（x’，y’）旋轉后的坐標，（x，y）原坐標，（x0，y0）旋轉中心，a旋轉的角度（順時針）

　　這種由輸入圖像通過映射得到輸出圖像的坐標，是向前映射。常用的向后映射是其逆運算

　　opencv實現圖片旋轉功能，非常簡單，幾行代碼即可：

　　#include《iostream》

　　#include《time.h》

　　#include《opencv2/opencv.hpp》

　　using namespace std;

　　using namespace cv;

　　inline double cpu_time（）{

　　return clock（）*1000/CLOCKS_PER_SEC;

　　}

　　//圖片旋轉操作

　　void imrotate（Mat& img， Mat& newIm， double angle）{

　　int len = max（img.cols， img.rows）;

　　Point2f pt（len/2.，len/2.）;

　　Mat r = getRotationMatrix2D（pt，angle，1.0）;

　　warpAffine（img，newIm，r，Size（len，len））;

　　//better performance ：

　　//Point2f pt（img.cols/2.，img.rows/2.）;

　　//Mat r = getRotationMatrix2D（pt，angle，1.0）;

　　//warpAffine（img，newIm，r，img.size（））;

　　}

　　int main（）{

　　Mat img = imread（“1.jpg”）;

　　//resize（img，img，Size（256，256））;

　　Mat newIm;

　　double t1，t2;

　　t1 = cpu_time（）;

　　//調用旋轉方法，模仿matlab，取名為imrotate

　　imrotate（img，newIm，15）;

　　t2 = cpu_time（）; c

　　out《《“Rotate one image cost： ”《《t2-t1《《“ ms”《《endl;

　　namedWindow（“Rotate”）;

　　imshow（“Rotate”，newIm）;

　　waitKey（10000）;

　　const string save_name = “rotate.jpg”;

　　imwrite（save_name，newIm）;

　　return 0;

　　}