電子發燒友App
?01
故事起源給定一個草坪區間的集合，為使區間互不重疊，最少需要移除多少個區間？
?
?簡單描述如下圖，最少移除多少個區間，可以使剩余的區間不重疊。
注：1、區間終點一定大于起點；2、區間[1,2]和[2,3]接觸，但不重疊。 ?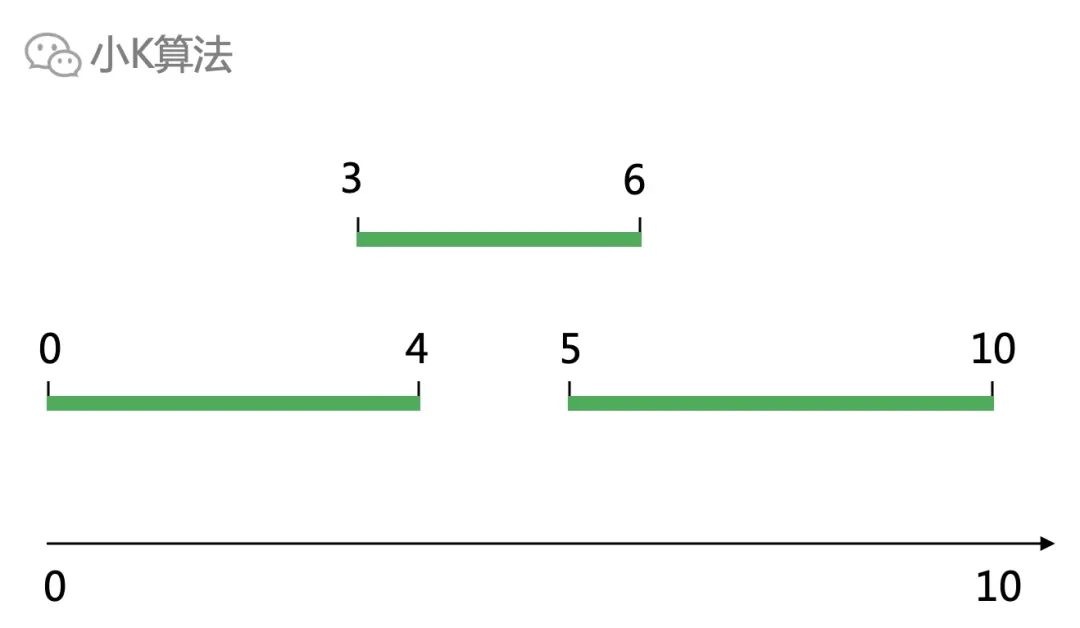
?
?02
分析題目求最少需要移除多少個，其實可以轉換問題，變成最多有多少個區間不重疊。
很多時候不容易直接求解時，都可以嘗試反向思考，這個技巧非常重要。 ?所以現在問題就是求最多有多少個區間，使他們落在x軸上不重疊。 ?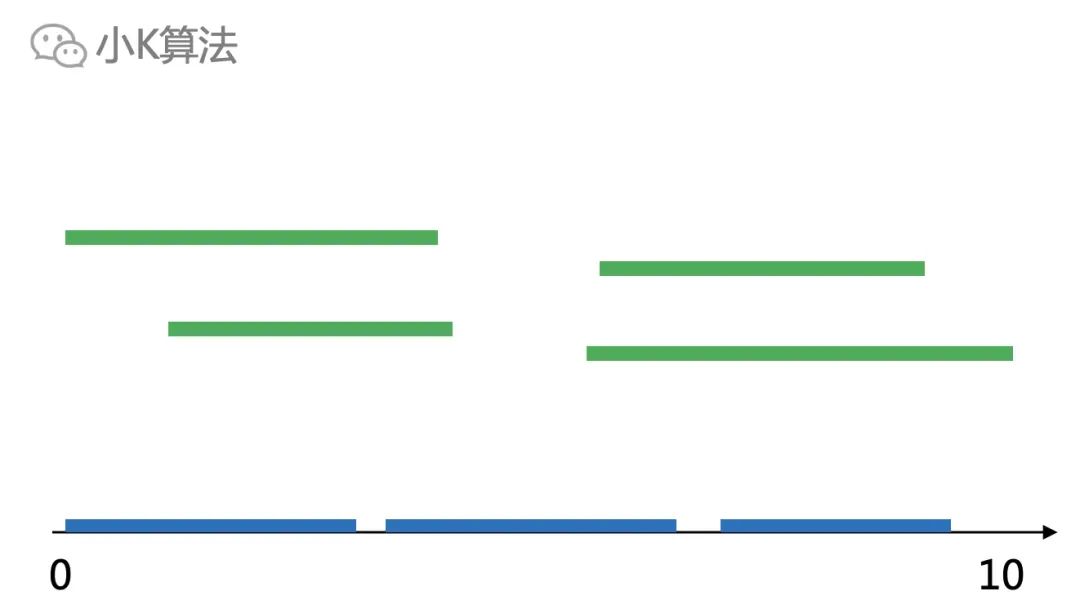
?
?03
最終狀態法這里給大家介紹一種非常重要的思考方法，小K稱之為“最終狀態法”。其本質就是先思考最終要得到的狀態，或者說正確結果應該是什么樣子。
?比如這個問題，假設我們已經求出了最優解，那這個最優解，一定是所有的區間中的k個區間，他們能平鋪在數軸上且不重疊。下面的藍色就是我們的答案。
?
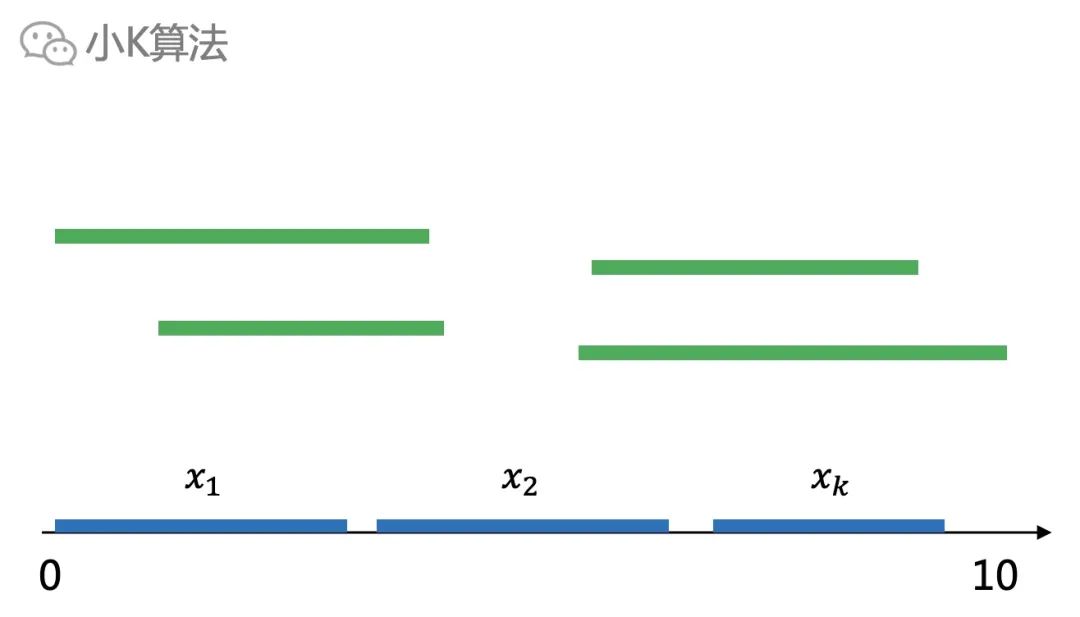?如果我在中間某個位置切一刀，分成兩個子問題。現在我問你：左邊區間中的解，是否仍然是左邊子問題的最優解呢？
?
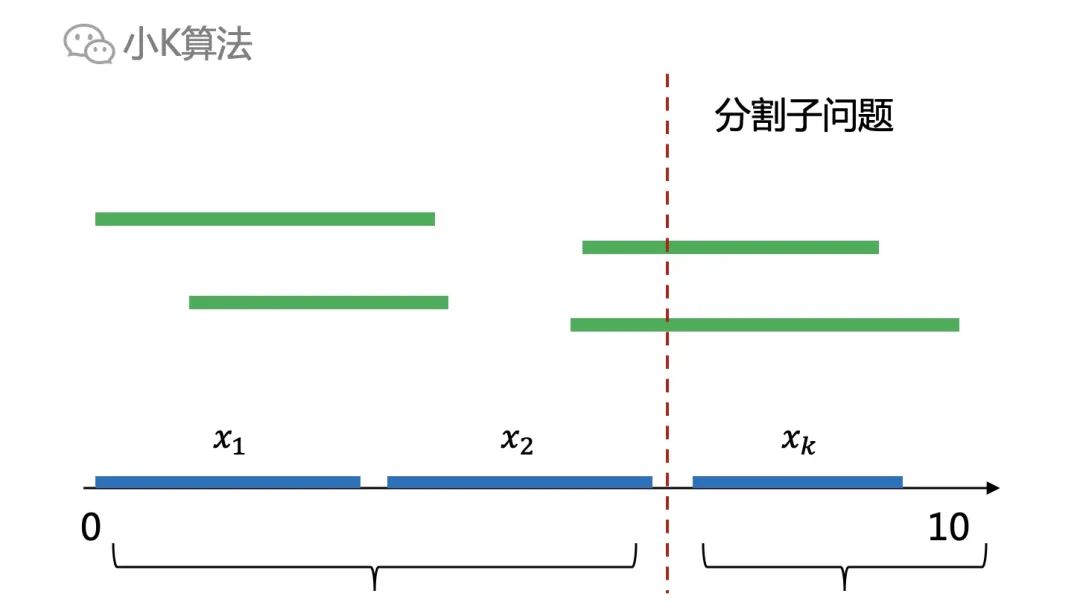?可以用反證法，先假設它不是最優解，那就意味著左邊一定還有更優的解，比如下面這樣，左邊可以選出3個區間。
?
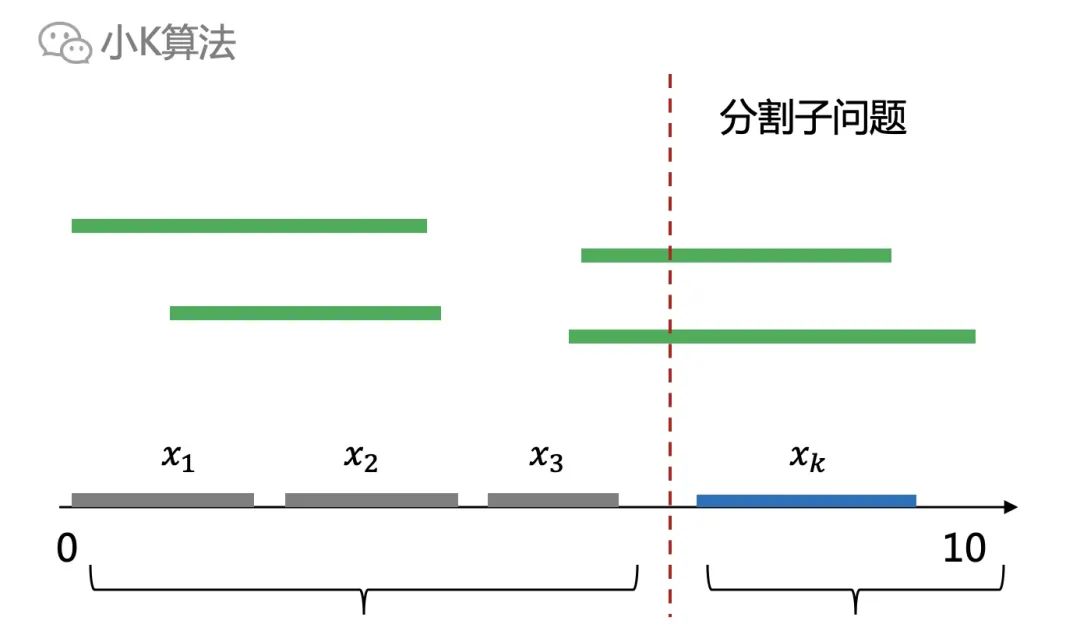?如果再把2個子問題組合起來，那整個問題的最優解應該是4個區間，這和我們之前假設的藍色是最優解矛盾了。說明分割子問題后，子問題的最優解也一定包含在整個問題的最優解中。
?反過來，我們求出了子問題的最優解，就可以遞推出大問題的最優解，這就是動態規劃的思想。
?
?
?04
動態規劃子問題是沿著數軸進行擴大的，有嚴格的順序關系，所以先對區間進行排序。
設f[i]表示前i個區間中，選擇第i個區間作為最后一個區間時的最優解，則f[i]=max(f[j])+1，其中區間j與區間i無重疊。
最大的f[i]就是我們要求的最優解。 ?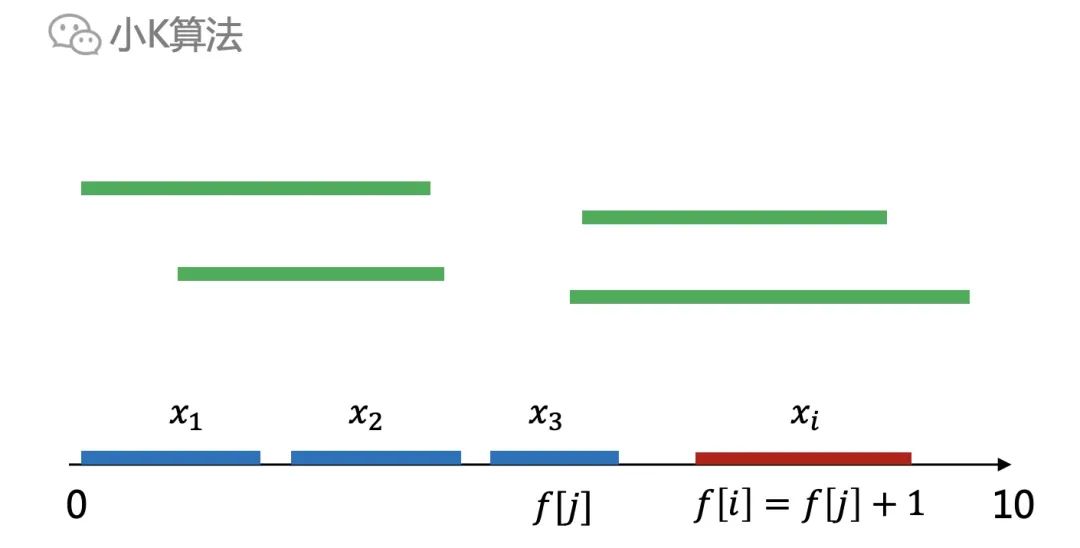
?通過遞推公式發現，這個模型跟最長上升子序列很像，如果我們把所有的區間繞起點逆時針旋轉90度如下，這不就是一個變種的LIS問題了嗎。
?
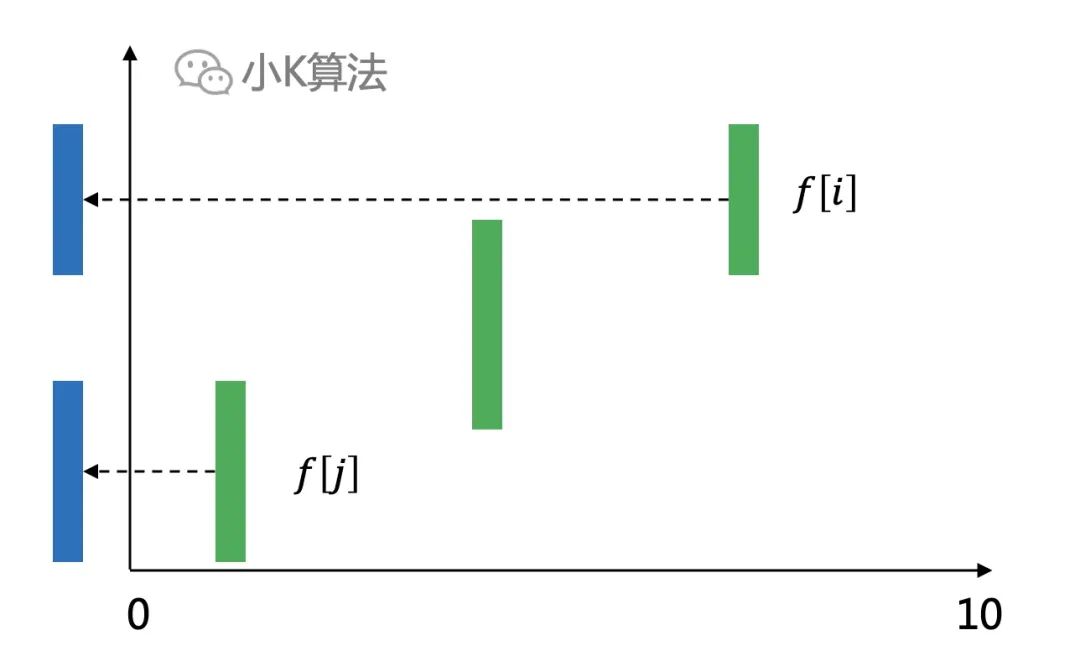?LIS問題可以看成是所有的區間起點都是0，只要求終點要大于之前的終點，而這個問題可以看成區間的起點都不一樣，且要求每個區間的起點要大于之前區間的終點。
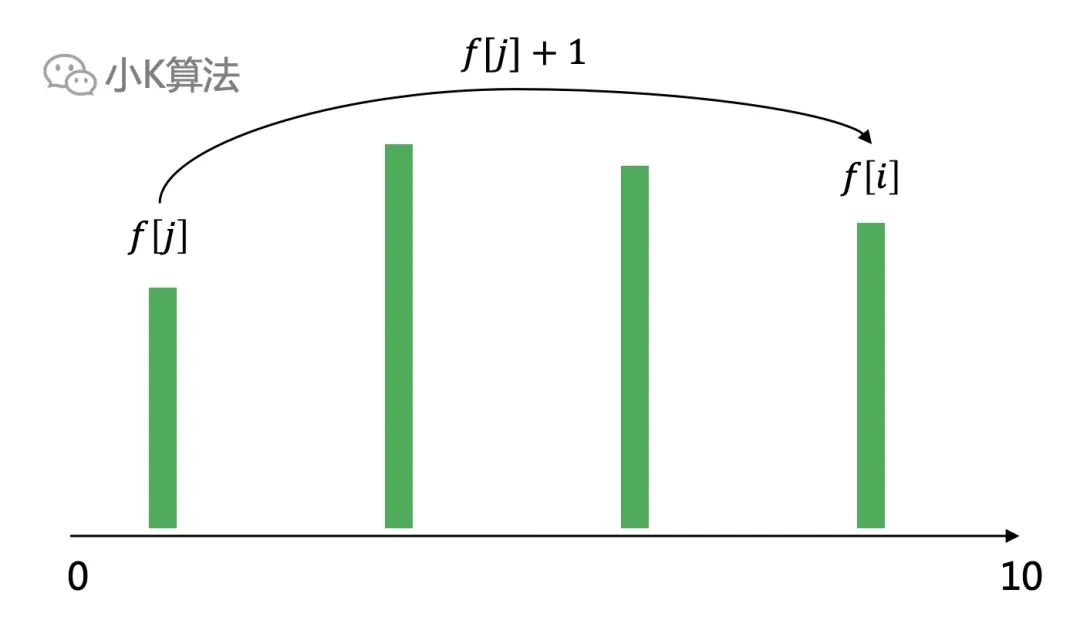?那他們之間的區別又有哪些呢？??
?1、LIS問題不能排序，因為每個位置都是一個點，所以必須在原來的順序上，找出最大遞增的數量。現在的問題都是區間，只求最終可以放下的數量，與順序無關，所以可以排序。
?2、LIS問題的f[i]可以由前面任意一個f[j]轉移過來。現在的問題如果排序完成后，其實不用枚舉前面所有的f[j]，因為前面一定比后面的小，更大的數軸區間一定可以放下更大的數量啊，所以f[i]其實完全可以從最近的f[j]直接轉移。
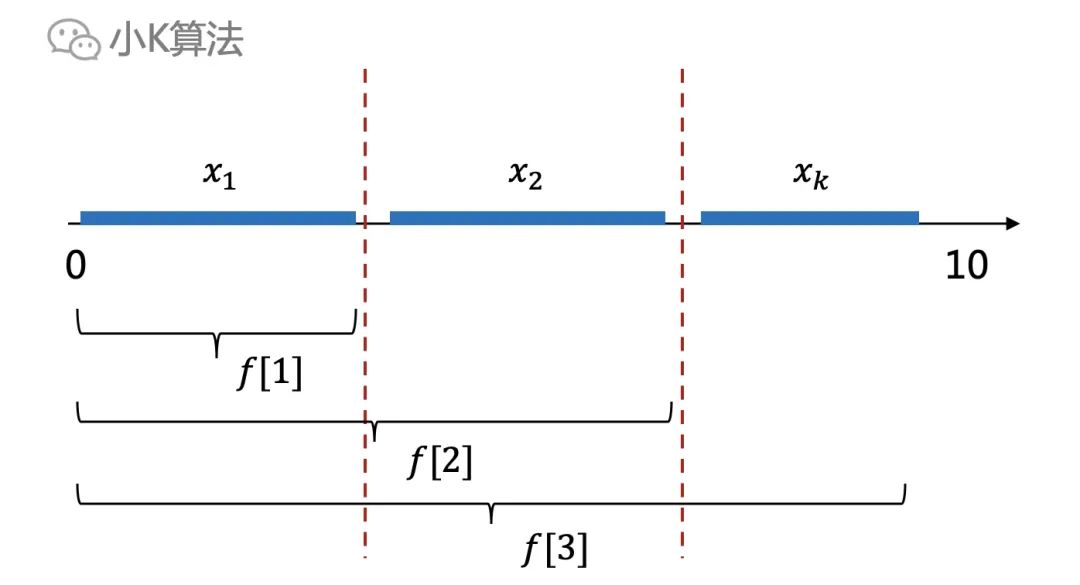
?比如下面，f[3]一定大于等于f[2]。
?
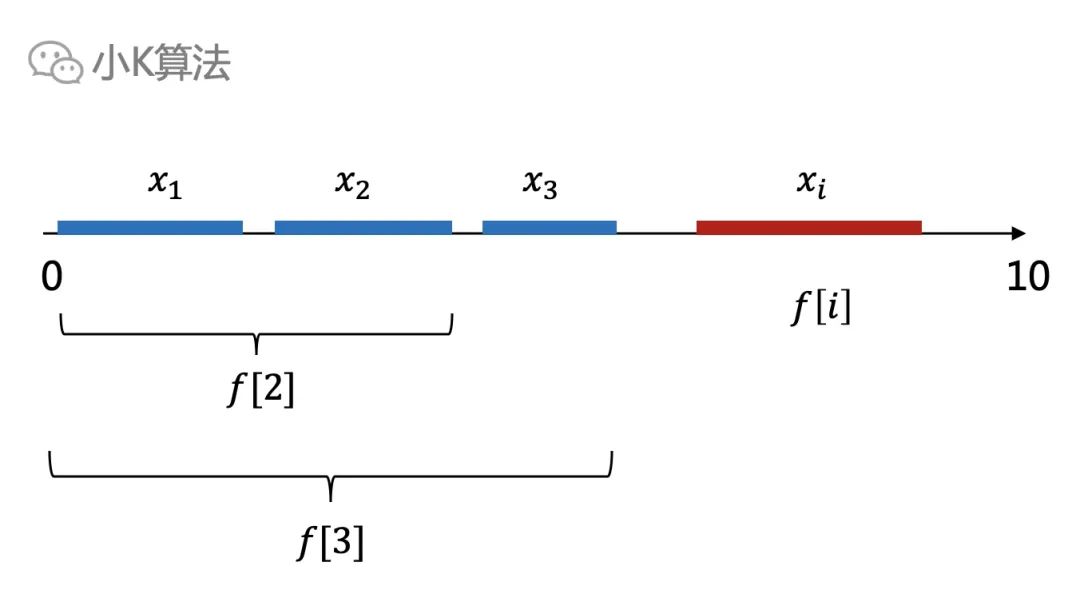?再換一種說法，如果在任何一個位置切一刀，前面是不是都是一個小規模的最優解。再加上前面的結論，每一步只需要從前一個轉移過來，這就意味著，每一步都是選擇最優的，而且最終得到的結果也是全局最優的。
?那這不就是貪心的思想了嗎，每一步都選擇當前最優的即可。
?
?
?05
貪心動態規劃的核心其實是對枚舉的優化，它本質也是枚舉了所有的情況，只是消除了重復子問題，所以一定能得到最優解。
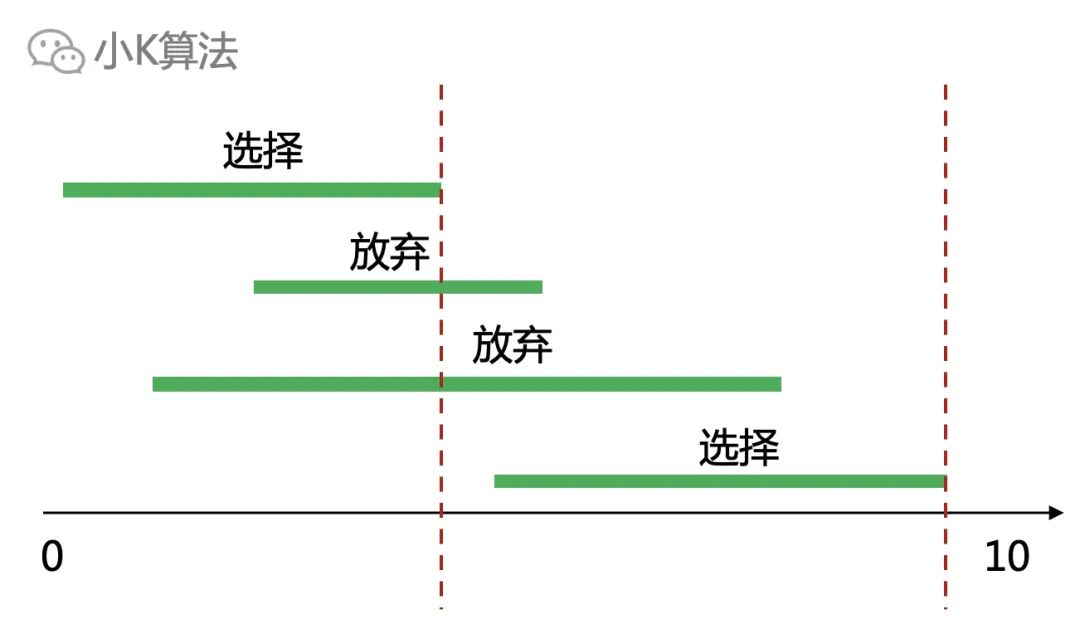
而貪心并不是計算了所有的情況，它是在每一步都選擇一個最優的，從而保證全局也是最優的。 ?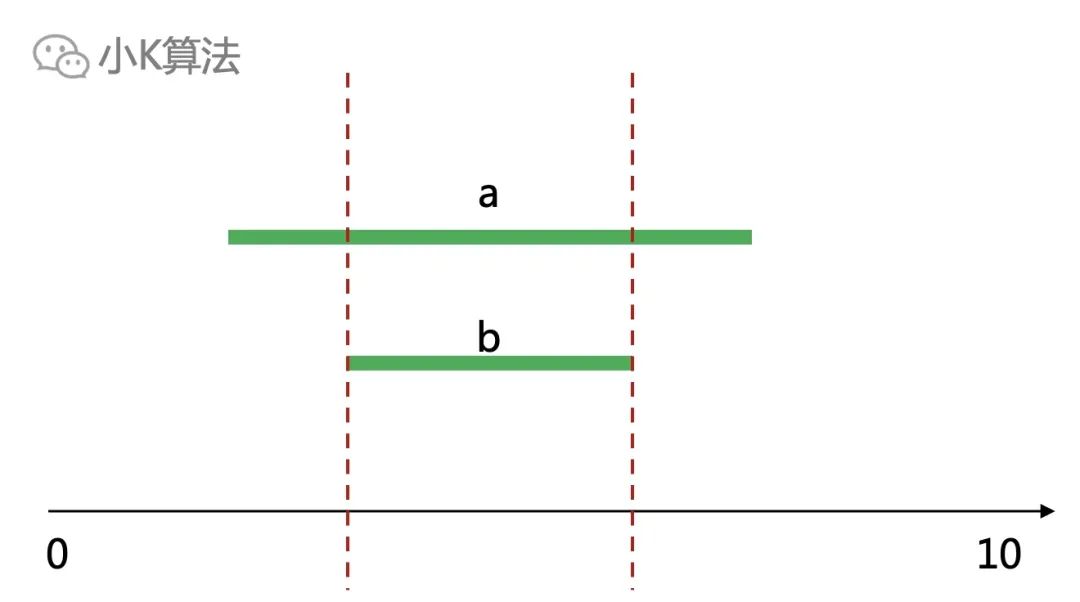
?再考慮應該選擇哪一個區間作為第一個區間呢？
如果按區間終點排序，則選擇a比選擇b更優，因為從左向右求每一步的最優解時，選擇a可以給后面的區間留下更多的空間。同理如果按起點排序，就從右向左掃描求解即可。 ?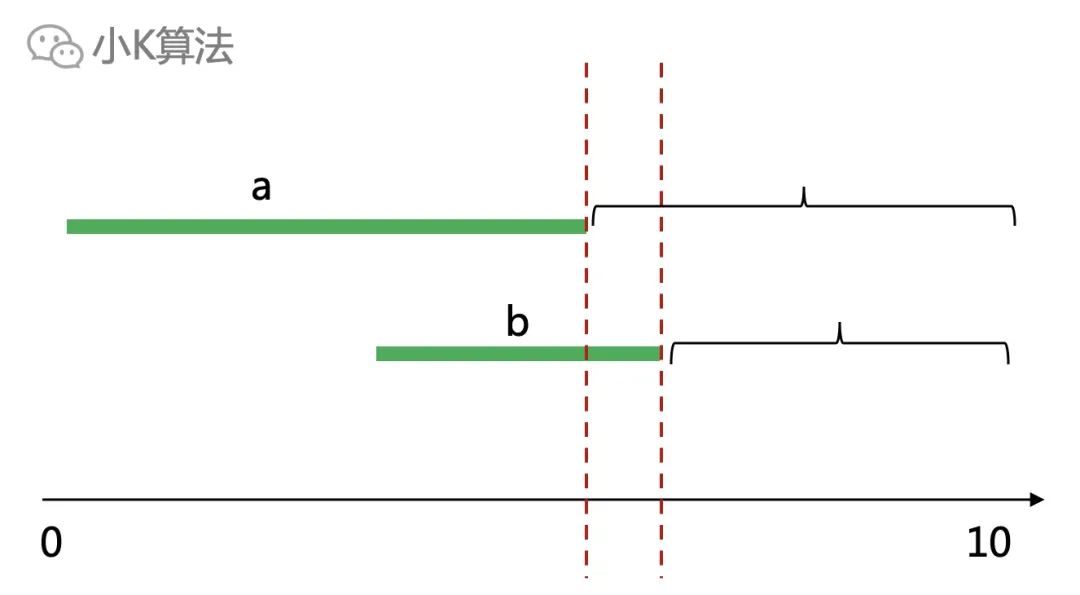
?
?
?簡單描述如下圖，最少移除多少個區間，可以使剩余的區間不重疊。注：1、區間終點一定大于起點；2、區間[1,2]和[2,3]接觸，但不重疊。 ?
?
?02
分析題目求最少需要移除多少個，其實可以轉換問題，變成最多有多少個區間不重疊。很多時候不容易直接求解時，都可以嘗試反向思考，這個技巧非常重要。 ?所以現在問題就是求最多有多少個區間，使他們落在x軸上不重疊。 ?
?
?03
最終狀態法這里給大家介紹一種非常重要的思考方法，小K稱之為“最終狀態法”。其本質就是先思考最終要得到的狀態，或者說正確結果應該是什么樣子。
?比如這個問題，假設我們已經求出了最優解，那這個最優解，一定是所有的區間中的k個區間，他們能平鋪在數軸上且不重疊。下面的藍色就是我們的答案。
?
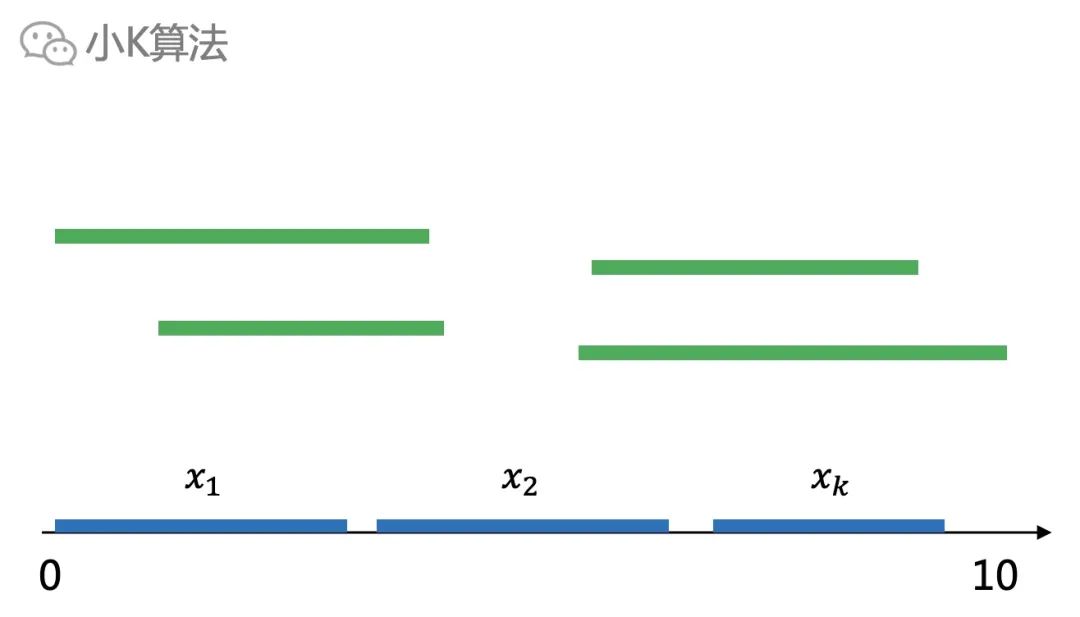?如果我在中間某個位置切一刀，分成兩個子問題。現在我問你：左邊區間中的解，是否仍然是左邊子問題的最優解呢？
?
?可以用反證法，先假設它不是最優解，那就意味著左邊一定還有更優的解，比如下面這樣，左邊可以選出3個區間。
?
?如果再把2個子問題組合起來，那整個問題的最優解應該是4個區間，這和我們之前假設的藍色是最優解矛盾了。說明分割子問題后，子問題的最優解也一定包含在整個問題的最優解中。
?反過來，我們求出了子問題的最優解，就可以遞推出大問題的最優解，這就是動態規劃的思想。
?
?
?04
動態規劃子問題是沿著數軸進行擴大的，有嚴格的順序關系，所以先對區間進行排序。設f[i]表示前i個區間中，選擇第i個區間作為最后一個區間時的最優解，則f[i]=max(f[j])+1，其中區間j與區間i無重疊。
最大的f[i]就是我們要求的最優解。 ?
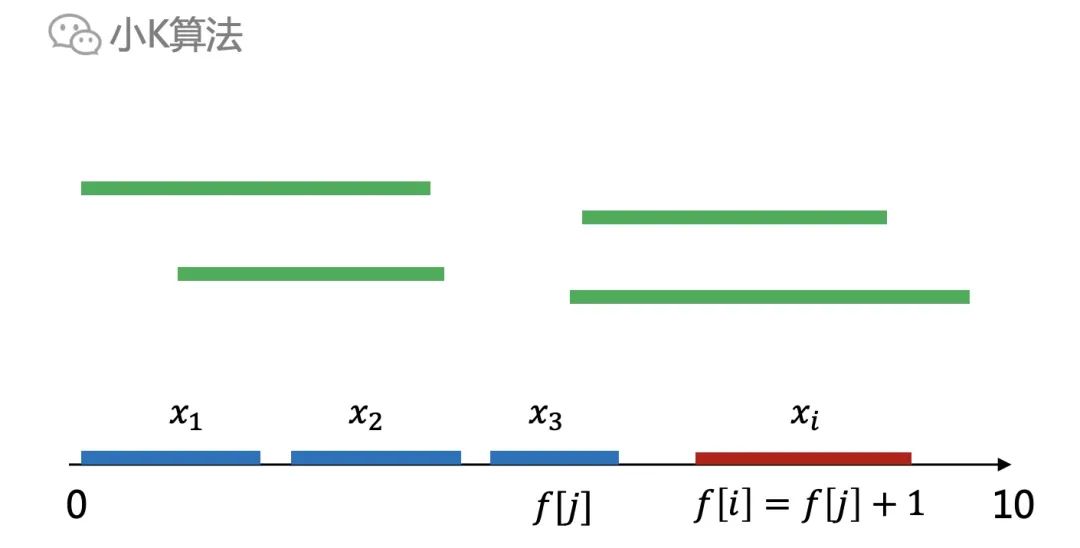?通過遞推公式發現，這個模型跟最長上升子序列很像，如果我們把所有的區間繞起點逆時針旋轉90度如下，這不就是一個變種的LIS問題了嗎。
?
?LIS問題可以看成是所有的區間起點都是0，只要求終點要大于之前的終點，而這個問題可以看成區間的起點都不一樣，且要求每個區間的起點要大于之前區間的終點。
?那他們之間的區別又有哪些呢？??
?1、LIS問題不能排序，因為每個位置都是一個點，所以必須在原來的順序上，找出最大遞增的數量。現在的問題都是區間，只求最終可以放下的數量，與順序無關，所以可以排序。
?2、LIS問題的f[i]可以由前面任意一個f[j]轉移過來。現在的問題如果排序完成后，其實不用枚舉前面所有的f[j]，因為前面一定比后面的小，更大的數軸區間一定可以放下更大的數量啊，所以f[i]其實完全可以從最近的f[j]直接轉移。
?比如下面，f[3]一定大于等于f[2]。
?
?再換一種說法，如果在任何一個位置切一刀，前面是不是都是一個小規模的最優解。再加上前面的結論，每一步只需要從前一個轉移過來，這就意味著，每一步都是選擇最優的，而且最終得到的結果也是全局最優的。
?那這不就是貪心的思想了嗎，每一步都選擇當前最優的即可。
?
?
?05
貪心動態規劃的核心其實是對枚舉的優化，它本質也是枚舉了所有的情況，只是消除了重復子問題，所以一定能得到最優解。而貪心并不是計算了所有的情況，它是在每一步都選擇一個最優的，從而保證全局也是最優的。 ?
?再考慮應該選擇哪一個區間作為第一個區間呢？如果按區間終點排序，則選擇a比選擇b更優，因為從左向右求每一步的最優解時，選擇a可以給后面的區間留下更多的空間。同理如果按起點排序，就從右向左掃描求解即可。 ?
?
??
5.3代碼實現 ?vector<vector<int>>?a(100,?vector<int>(2,?0)); bool?cmp(const?vector<int>?&u,?const?vector<int>?&v)?{ ????return?u[1]?1]; } int?main()?{ ????int?n; ????cin?>>?n; ????for?(int?i?=?0;?i?cin?>>?a[i][0]?>>?a[i][1]; ????} ????a.resize(n); ????sort(a.begin(),?a.end(),?cmp); ????int?ans?=?1,?right?=?a[0][1]; ????for?(int?i?=?1;?i?if?(a[i][0]?>=?right)?{ ????????????right?=?a[i][1]; ????????????ans++; ????????} ????} ????cout?<endl; ????return?0; } ? ?06 總結這個問題難度不大，但卻有很多可以思考的東西在里面，如果直接看問題肯定和LIS沒有任何聯系，但通過公式發現其本質還是有一些聯系在里面。類似的思想很常見，比如如果發現問題符合這種模型，那就又可以用之前寫過的一篇LIS問題的優化技巧，單調隊列+二分來進行模型的優化。當然算法問題不應太注重固定的套路模型，思考方法才是更重要的，以不變應萬變。 ? ?
審核編輯 ：李倩
工商網監
評論