PID控制是最早發展起來的控制策略之一，因為它所涉及的設計算法和控制結構都很簡單，因此，被廣泛應用于過程控制和運動控制中。但在實際系統設計過程中，設計師經常受到參數整定方法繁雜的困擾，PID控制器參數往往因整定不良、性能欠佳，對運行工況的適應性很差。而計算機技術和控制理論的發展為PID控制器參數的整定提供了新的途徑。

　　MATLAB是一種高性能的數值計算和可視化軟件，它集數值分析、矩陣運算和圖形顯示于一體，構成了一個靈活、綜合、具有豐富特性的控制系統設計環境。借助于MATLAB設計環境可以直觀、方便地對系統進行分析、計算，輕松解決PID參數整定設計工作。

　　Simulink是用于MATLAB下建立系統框圖和仿真的環境。Simulink是—個交互式動態系統建模、仿真和分析圖形環境，是一個進行基于模型的嵌入式系統開發的基礎開發環境。Simulink可以針對控制系統等進行系統建模、仿真、分析等工作。借助于Simulink仿真環境，可以為PID參數整定工作提供極大的方便。本文以基于MATLAB／Simulink環境進行臨界比例度法PID參數整定為例，說明在PID參數整定過程中，借助于Simulink環境，非常直觀、可以隨意修改仿真參數，節省了大量的計算和編程工作量。

　　PID 控制系統原理及算法

　　當我們不能將被控對象的結構和參數完全地掌握，或者是不能得到精確的數學模型時，在這種情況下最便捷的方法便是采用PID 控制技術。為了使控制系統滿足性能指標要求，PID 控制器一般地是依據設定值與實際值的誤差，利用比例（P）、積分（I）、微分（D）等基本控制規律，或者是三者進行適當地配合形成相關的復合控制規律，例如，PD、PI、PID 等。

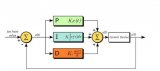
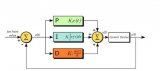
　　圖1 是典型PID 控制系統結構圖。在PID 調節器作用下，對誤差信號分別進行比例、積分、微分組合控制。調節器的輸出量作為被控對象的輸入控制量。

　　PID 控制器主要是依據給定值r（t）與實際輸出值y（t）構成控制偏差，用公式表示即e（t）=r（t）-y（t），它本身屬于一種線性控制器。通過線性組合偏差的比例（P）、積分（I）、微分（D），將三者構成控制量，進而控制受控對象。控制規律如下：

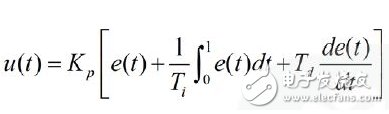
　　其傳遞函數為：

　　式中：Kp--比例系數； Ti--積分時間常數； Td--微分時間常數。

　　PID控制器參數對控制性能的影響

　　1）比例系數

　　比例系數Kp加大，會使系統的響應速度加快，減小系統穩態誤差，從而提高系統的控制精度。過大的比例系數 會使系統產生超調，并產生振蕩或使振蕩次數增多，使調節時間加長，并使系統穩定性變壞或使系統變得不穩定。當Kp太小時，又會使系統的動作緩慢。

　　2）積分時間常數

　　一般不單獨采用積分控制器，通常與比例控制或比例微分控制聯合作用，構成PI控制或PID控制。積分作用的強弱取決于積分時間常數Ti 的大小，Ti越小，積分作用越強，反之則積分作用弱。增大積分時間常數 ，有利于減小超調，減小振蕩，使系統更穩定，但同時要延長系統消除靜差的時間。積分時間常數太小會降低系統的穩定性，增大系統的振蕩次數。

　　3）微分時間常數

　　微分控制作用只對動態過程起作用，而對穩態過程沒有影響，且對系統噪聲非常敏感，所以單一的微分控制器都不宜采用。通常與比例控制或比例積分控制聯合作用，構成PD控制或PID控制。微分作用的強弱取決于微分時間常數Td 的大小，Td越大，微分作用越強，反之則越弱。微分時間常數 偏大或偏小時，系統的超調量都較大，調節時間都較長，只有選擇合適的 ，才能獲得比較滿意的過度過程。

　　從PID控制器的3個參數的作用可以看出3個參數直接影響控制效果的好壞，所以要取得較好的控制效果，就必須合理的選擇控制器的參數。總之，比例控制主要用于偏差的“粗調”，保證控制系統的“穩”；積分控制主要用于偏差的“細調”，保證控制系統的“準”；微分控制主要用于偏差的“細調”，保證控制系統的“快” 。

　　3 臨界比例度法

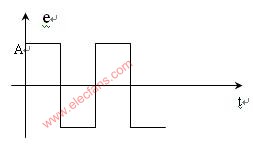
　　Ziegler和Nichols提出的臨界比例度法是一種非常著名的工程整定方法。通過實驗由經驗公式得到控制器的近似最優整定參數，用來確定被控對象的動態特性的兩個參數：臨界增益Ku 和臨界振蕩周期Tu 。臨界比例度法?適用于已知對象傳遞函數的場合，在閉合的控制系統里，將控制器置于純比例作用下，從大到小逐漸改變控制器的比例增益 ，得到等幅振蕩的過渡過程。此時的比例增益 被稱為臨界增益 ，相鄰兩個波峰間的時間間隔為臨界振蕩周期Tu。

　　用臨界比例度法整定PID參數的步驟如下：

　　（1） 將控制器的積分時間常數 置于最大（Ti =?），微分時間常數 置零（Td=0），比例系數Kp 置適當的值，平衡操作一段時間，把系統投入自動運行。

　　（2）將比例增益Kp逐漸減小，直至得到等幅振蕩過程，記下此時的臨界增益Ku和臨界振蕩周期Tu值。

　　（3）根據Ku和Tu值，按照表l中的經驗公式，計算出控制器各個參數，即Kp、Ti 和Td的值。

　　按照“先P后I最后D”的操作程序將控制器整定參數調到計算值上。若還不夠滿意，則可再進一步調整。

　　PID 控制器的MATLAB 仿真

　　美國MathWorks 公司推出的MATLAB 是一套具備高性能的數值計算和可視化軟件。由于MATLAB 可以將矩陣運算、圖形顯示、信號處理以及數值分析集于一體，構造出的用戶環境使用方便、界面友好，因此MATLAB 受到眾多科研工作者的歡迎。本文利用MATLAB 仿真工具箱Simulink 的功能，在基于仿真環境Matlab/Simulink 工具上用圖形化方法直接建立仿真系統模型，啟動仿真過程，將結果在示波器上顯示出來。

　　仿真實例分析

　　建立數學建模

　　設被控對象等效傳遞函數為

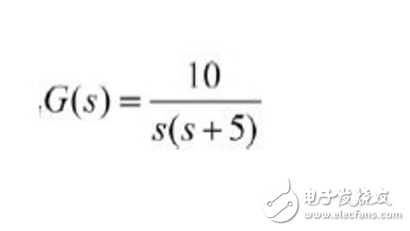
　　仿真建模

　　仿真建模的目的就是將數學模型轉換成計算機能夠執行的模型，運用Simulink 可以達到此目的。圖2 是綜合圖1 和給定計算公式運用Simulink 建立的PID 控制的連續系統的仿真模型（建模步驟略）。

　　仿真實驗

　　在傳統的PID 調節器中，參數的整定問題是控制面臨的最主要的問題，控制系統的關鍵之處便是將Kp、Ti、Td三個參數的值最終確定下來。而在工業過程控制中首先需要對PID 控制中三參量對系統動態性的影響進行實際深入地了解，才能確定怎樣將三參數調節到最佳狀態。在本實驗中，對各參量單獨變化對系統控制作用的影響進行討論，其中在對一個參量變化引發的影響進行討論時，需要將其余兩個參數設定為常數。

　　P 控制作用分析

　　分析比例控制作用。設Td= 0、Ti=∞、Kp= 3 ~ 10.輸人信號階躍函數，分別進行仿真，如圖3 所展示的系統的階躍響應曲線。

　　圖3 顯示的仿真結果表明：系統的超調量會隨著Kp值的增大而加大，系統響應速度也會會隨Kp值的增大而加快。但是系統的穩定性能會隨著Kp的增大而變差。

　　比例積分控制作用的分析

　　設比例積分調節器中Kp= 1，討論Ti= 0.01 ~ 0.05 時。輸人信號階躍函數，分別進行仿真，如圖4 所展示的系統的系統的階躍響應曲線。

　　系統的超調量會隨著Ti值的加大而減小，系統響應速度隨著Ti值的加大會略微變慢。

　　 微分調節作用的分析

　　設Kp= 1、Ti= 0.01，討論Td= 10 ~ 100 時對系統階躍響應曲線的影響。輸人信號階躍函數，分別進行仿真，如圖5 所展示的系統的階躍響應曲線。

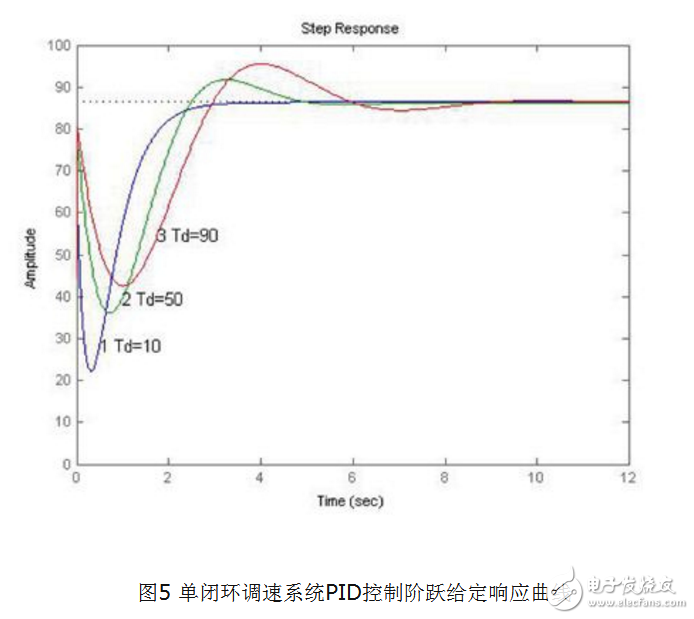
　　結論

　　（1）對于PID 參數采用MATLAB 進行整定和仿真，使用起來不僅快捷、方便，而且更為直觀，同時也避免了傳統方法反復修改參數調試。

　　（2）系統的響應速度會隨Kp值的增大而加快，同時也有助于靜差的減小，而Kp值過大則會使系統有較大超調，穩定性變壞；此外，系統的動作會因為過小的Kp值減慢。

　　（3）超調的減小、振蕩變小以及系統穩定性的增加都取決于積分時間Ti的增大，但是系統靜差消除時間會因為Ti的增大而變長。

　　（4）增大微分時間Td對于系統的穩定性、系統響應速度的加快以及系統超調量的減小都會有所幫助。但是如果Td過大，則會使得調節時間較長，超調量也會增大；如果Td過小，同樣地也會發生以上狀況。

　　（5）總之PID 參數的整定必須考慮在不同時刻三個參數的作用以及彼此之間的作用關系。

　　PID 控制應用領域極為廣泛，可將其應用于電力、化工、輕工、冶金以及機械等工業過程控制中。通常情況下，最適合采用PID 控制技術的條件是：當我們對目標系統或被控對象的內部特征不完全清楚時，或者是系統的全部參數不能經過有效的測量手段來獲取，同時必須依賴于經驗和現場調試來確定系統控制器的結構參數情況下采用該技術。