計算機中常用幾種不同的進位數制,包括二(八、十六)進制和十進制。二進制數據更容易用邏輯線路處理,更接近計算機硬件能直接識別和處理的電子化信息的使用要求,而使用計算機的人更容易接受十進制的數據類型。二者之間的進制轉換是經常遇到的問題,應熟練掌握。
(1)二 (八、十六) 進制 十進制數據轉換
公式 (2.3) 確定的運算規則,是不同進位計數制數據之間完成進位制轉換的依據。
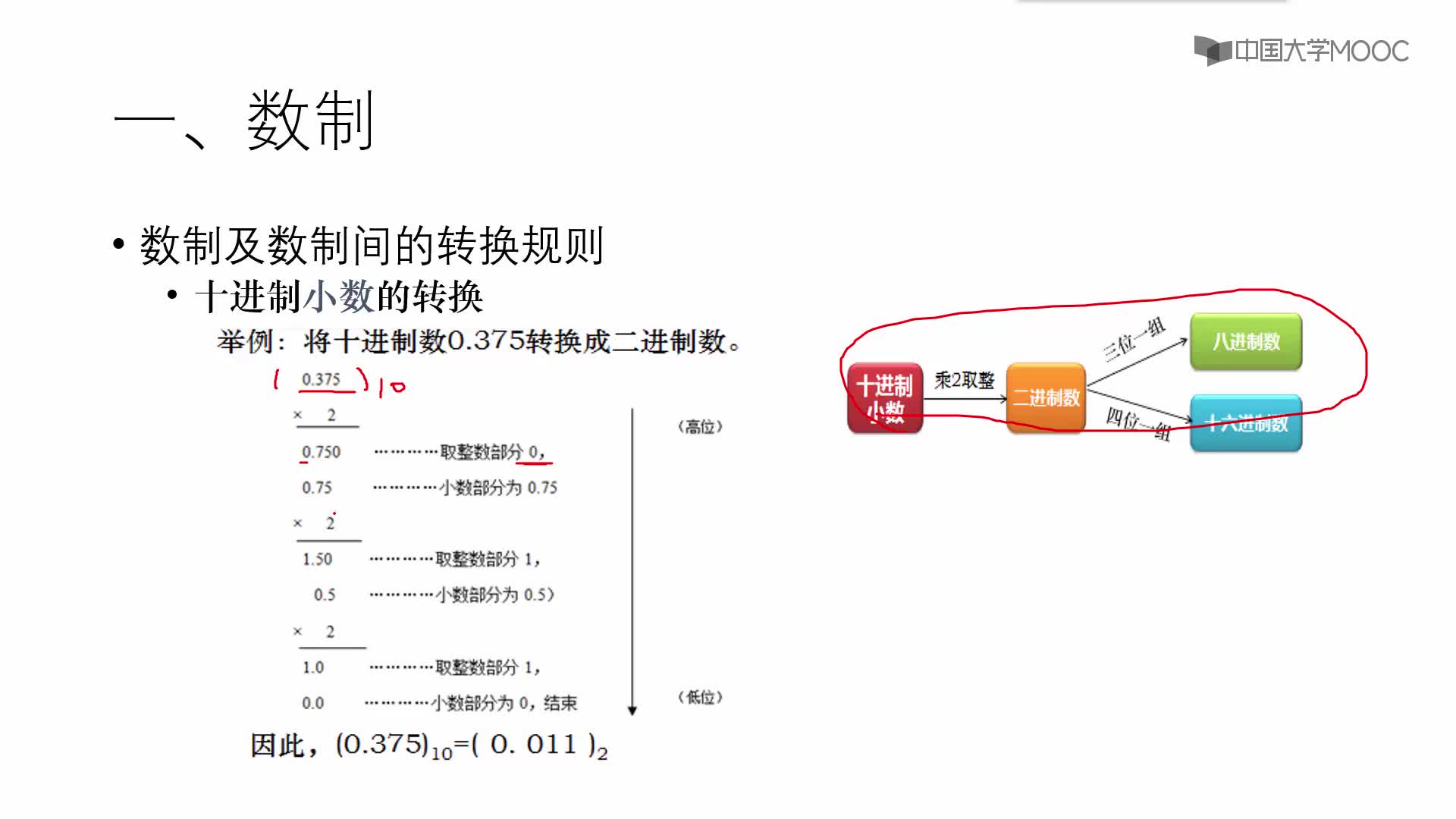
十進制到二進制的轉換,通常要區分數的整數部分和小數部分,并分別按除2取余數部分和乘2取整數部分兩種不同的方法來完成。
對整數部分,要用除2取余數辦法完成十→二的進制轉換,其規則是:
用2除十進制數的整數部分,取其余數為轉換后的二進制數整數部分的低位數字;
再用2去除所得的商,取其余數為轉換后的二進制數高一位的數字;
重復執行第二步的操作,直到商為0,結束轉換過程。
例如, 將10進制的37轉換成二進制整數的過程如下:
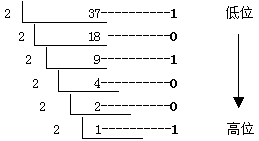
余數部分,即轉換后的結果,為(100101) 2。
對小數部分,要用乘2取整數辦法完成十→二的進制轉換,其規則是:
用2乘十進制數的小數部分,取乘積的整數為轉換后的二進制數的最高位數字;
再用2乘上一步乘積的小數部分,取新乘積的整數為轉換后二進制小數低一位數字;
重復第二步操作,直至乘積部分為0,或已得到的小數位數滿足要求,結束轉換過程。
例如,將十進制的0.43,轉換成二進制小數的過程如下(假設要求小數點后取5位):
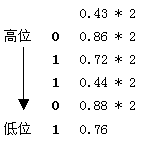
整數部分,即轉換后的二進制小數為(0.01101)2。
對小數進行轉換的過程中,轉換后的二進制已達到要求位數,而最后一次的乘積的小數部分不為0,會使轉換結果存在誤差,其誤差值小于求得的最低一位的位權。
對既有整數部分又有小數部分的十進制數, 可以先轉換其整數部分為二進制數的整數部分,再轉換其小數部分為二進制的小數部分,通過把得到的兩部分結果合并起來得到轉換后的最終結果。例如,(37.43)10 = (100101.01101)2 。
在實現手工轉換時,如果對二進制數已經比較熟悉,基本上記住了以2為底的指數值,即二進制數每一位上的權,對十進制數進行轉換時,也可以不采用上述規則,基本上可以直接寫出來。例如,
(45.625)10=32+8+4+1+0.5+0.125=(10 1 1 01. 10 1) 2,即(101101.101)2。
(1105)10 = 1024+81 = 1024+ 64+16 + 1= (1000 10 10001) 2,即(10001010001)2。
參照上述方法,也可以實現十→八進制, 十→十六進制的轉換過程。例如,
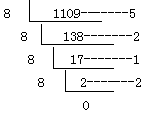
結果:(1109)10 =(2125)8
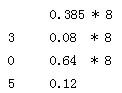
結果:(0.385)10 =(0.305)8
完成 十→十六 進制數的轉換方法與前述方法類似,只是乘除16時,手工運算不大方便。
(2) 二 八 及 二 十六的進制轉換
用二進制表示一個數值N,所用的位數K為log2N,如表示4096, K為13,寫起來位串較長。為此,計算機中也常常采用八進制和十六進制來表示數值數據,為表示數值N,分別有如下對應關系:
m-1
N = ∑ Di * 8i (2.5) Di 的取值為0到7
i = -k
例如 (7.44)8 = 7*80 + 4*8-1 + 4*8-2 = (7.5625)10 。
m-1
N = ∑ Di * 16i (2.6) Di 的取值為0到9和A到F
i = -k
例如 (1A.08) 16 = 1*161 + 10*160 + 8*16-2 = (26.03125)10 。
上述二式中所用符號的意義與公式(2.3)中所用符號的意義類同,但此處Di包含的基本符號分別限于0-7和0-9、A-F,各位的碼權分別為8i和16i
把用二進制、八進制、十六進制表示的數轉換成10進制數的值, 使人能更容易地衡量這個數值的大小。
二進制數與八進制、十六進制數的關系
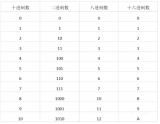
由于log28=3, log216=4, 即一位8進制的數可以用3位二進制的數重編碼來得到, 一位16進制的數可以用4位二進制的數重編碼得到, 故人們通常認為, 在計算機這個領域內, 8進制和16進制數, 只是二進制數的一種特定的表示形式。表2.1給出少量二、八、十六和十進制數的對應關系:
表2.1 二、八、十六和十進制的對應關系
|
二進制數 |
八進制數 |
十六進制數 |
十進制數的值 |
|
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
00 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
在把二進制數轉換成八進制或十六進制表示時,應從小數點所在位置分別向左、向右對每三位或每四位二進制位進行分組,寫出每一組所對應的一位八或十六進制數。若小數點左側(即整數部分)的位數不是3或4的整數倍,可以按在數的最左側補零的方法理解;對小數點右側(即小數部分),應按在數的最右側補零的方法處理,否則容易轉換錯。對不存在小數部分的二進制數(整數),應從最低位開始向左把每3位劃分成一組,使其對應一個八進制位,或把每4位劃分成一組,使其對應一個十六進制位,例如:
(10.101) 2 變成八進制時,應把它理解為(010.101)2,是(2.5)8 , 即八進制的2.5。當把它轉換為十六進制時,應首先變為(0010.1010)2,是(2.A) 16,即十六進制的2.A,而不是(2.5)16。又如,
(1100111.10101101) 2 = (147.532) 8
(1100111.10101101) 2 = (67.AD)16
八和十六進制之間的轉換不怎么常用,經過二進制的中間結果進行轉換是方便的。
 電子發燒友App
電子發燒友App

























































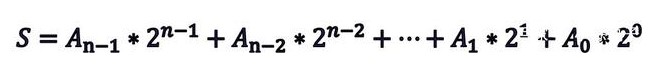












評論