什么是混聯電路

　　混聯，是指既有串聯又有并聯的結構方式，在電路、機床、混合動力系統等中常用。其中電路即叫混聯電路。方式為串聯電路和并聯電路。

　　混聯電路的分析方法

　　首先明確電路各部分的連接方法，然后分析出局部電路電阻的變化對電路總電阻的影響，進而分析出電路總電流的變化，由總電流的變化分析各部分電壓的變化，由各部分電壓的變化分析局部電路上電流變化思路為：局部電阻變化→總電阻變化→總電流變化→各部分電壓變化→局部電流變化。

　　分析總電阻變化時注意：

　　（1）電阻串聯：其中之一變大，串聯電路總電阻變大；其中之一變小，總電阻也變小。

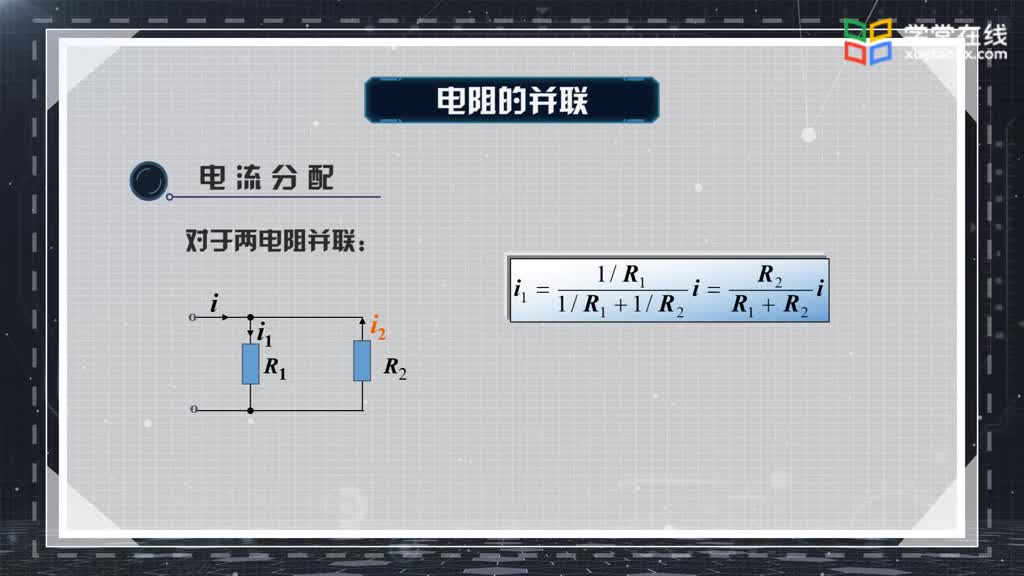
　　（2）電阻并聯：其中之一變大，并聯電路總電阻變大；其中之一變小，總電阻也變小。

　　混聯電路的分析與計算

　　一）節點法

　　該法是簡化混聯電阻電路最有效的且用得最多的一種方法。它采用四個步驟：

　　1．確定計算哪兩端間的電阻。

　　2．找出電路中的獨立節點（節點：三條或三條以上支路的連接點）。電路中有直接用導線連接的兩點，應視為同一個點（即等電位點）。

　　3．把各節點、兩端點豎直（或水平）排列。兩端點位于最外層。

　　4．連接節點間、端點間和節點與端點間的電阻。連接兩節點間、兩端點間和節點與端點間的電阻時，不能穿過其他節點或端點。

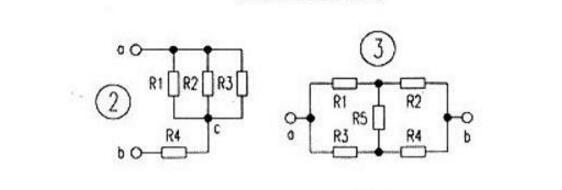
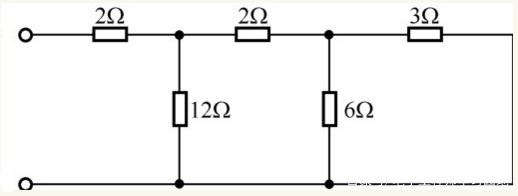
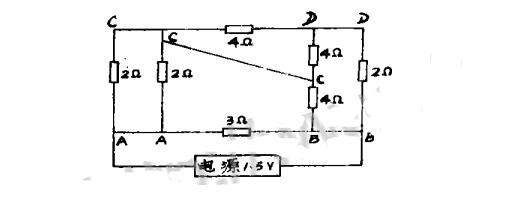
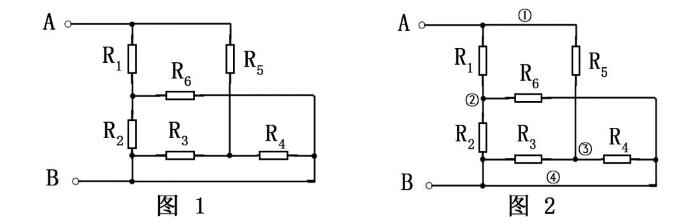
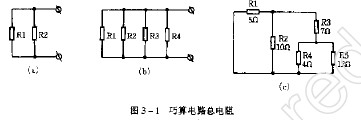
　　例：如圖1電路中，已知R1=R2=R3=R4=6Ω，求電路中a、b間的電阻？

　　分析：利用節點法，就可將圖l原電路等效為圖2所示電路，由圖2可知，R1、R2電阻與R3并聯后，再與R4串聯，即為a、b間的電阻Rab。

　　解：∵1／R123=1／R1+1／R2+1／R3=1／6十1／6+1／6=1／2

　　R123=2Ω

　　Rab=R123+R4=6Ω+2Ω=8Ω．

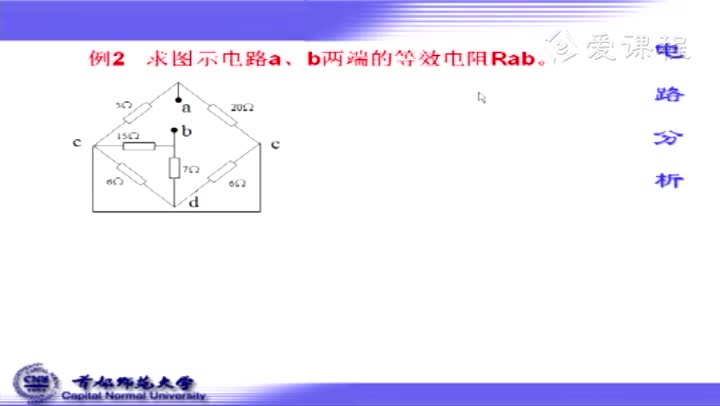
　　二）平衡電橋等效法

　　該法是簡化具有平衡電器橋路最有效的一種方法。它利用電橋電路平衡時，橋支路可視為開路或短路的原理來實現將原混聯電阻電路向串聯并聯電阻電路的等效變換。

　　電橋電路如圖3所示，由電阻R1～R5構成的電路就是一個電橋電路。其中由電阻R5構成的支路，稱為“橋支路”：由電阻R1一R4各自構成支路，稱為“橋臂支路”，電阻R1～R4稱為“橋臂電阻”。

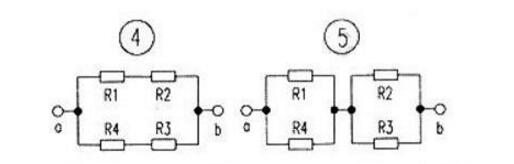
　　電橋平衡時，橋支路可視為開路或短路，這是因為當橋支路的電流為零或橋支路兩端電位相等時，電橋平衡。所以電橋平衡時，當橋支路的電流為零時，橋支路當然可視為開路（如圖4）：當橋支路兩端電位相等時，橋支路當然可視為短路（如圖5）。

　　怎樣確定電橋電路是否平衡呢？在電橋電路中，當相對“橋臂電阻”乘積相等（或相鄰“橋臂電阻”比值相等），則原電橋電路平衡（可推導）。

　　通過以上分析．利用本法化簡帶平衡電橋的混聯電阻電路只用兩個步驟：1、利用電橋電路平衡條件確定電橋式混聯電阻電路是否平衡。2、如果原電路是平衡的，對橋支路進行開路或短路的等效處理。

　　例：如圖3所示電路中，已知R1=20Ω，R2=40Ω，R3=60Ω，R4=30Ω，R5=50Ω，求電路中a、b間的電阻？

　　分析：先對原電橋電路進行平衡判斷，如果原電路是平衡的．對橋支路進行開路等效處理。按圖4電路進行計算（當然也可按圖5處理）。由圖4電路可知，電阻R1與R2，電阻：R3與R4先串聯，然后再并聯即為a、b間的電阻。

　　解：∵R1·R3=20×60=1200（Ω）

　　R2·R4=40×30=1200（Ω）

　　R1·R3=R2·R4

　　∴該電橋電路平衡

　　原電橋電路（圖3）等效為圖4電路

　　R12=Rl+R2=201Ω+40Ω=60Ω

　　R34=R3+R4=60Ω+30Ω=90Ω

　　Rab=R12·R34／（R12+R34）=（60x90）／（60+90）=36（Ω）