控制系統是制導炸彈的關鍵部位。目前，所有制導炸彈的控制系統都是基于一定的數學模型，以固定的方式修正彈道誤差。由于存在各種不可預知的誤差因素，但控制方式卻不可調整，造成制導炸彈的實際命中精度不高。基于此，提出了一種新的制導炸彈智能控制系統，該系統引入具有前置濾波特性的非單點模糊化技術，針對非單點模糊推理系統內部參數不易調整的問題，提出用梯度下降算法和遺傳算法構成的混合并行學習算法調整系統內部參數，從而能夠自動處理受噪聲影響的訓練數據，提高命中精度。通過計算機仿真試驗，并與基于ANFIS的制導炸彈智能控制系統進行比較，驗證了該控制系統的有效性。

　　1 非單點模糊推理系統(NSFIS)

　　提出的制導炸彈智能控制系統的核心是非單點模糊推理系統(NSFIS)。一個n輸入1輸出的模糊推理系統，其模糊規則可表述如下

上的模糊集合，

和y∈V對應于系統輸入和輸出變量，l=1，2，…，M為模糊規則數。

?

　　當采用中心平均模糊消除器、乘積推理規則、高斯隸屬度函數和非單點模糊化時，得到的非單點模糊推理系統為

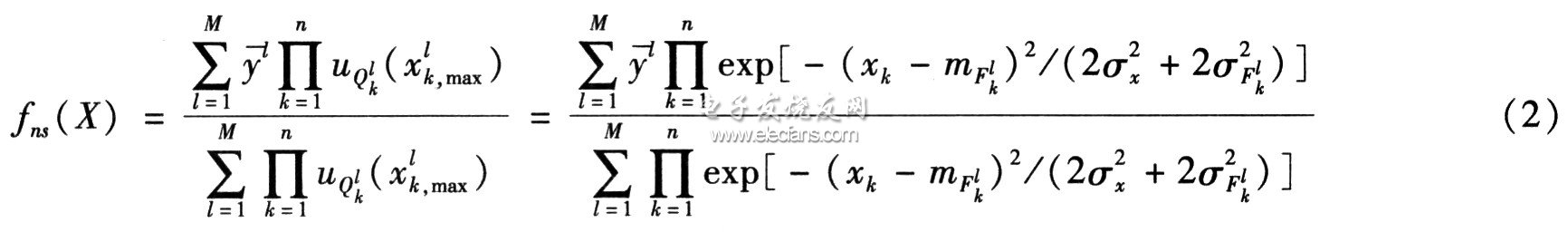
時，非單點模糊化與單點模糊化等價;當輸入變量xk受到噪聲污染時，噪聲在非單點模糊器中會被因子

所克服。如果σx≥σFkl，噪聲將會在很大程度上被抑制。

?

　　2 NSFIS的參數學習算法

　　模糊推理系統是高度非線性系統，在對復雜系統建模的過程中，其內部參數

主要依靠某種學習算法對輸入一輸出數據對進行訓練來確定。目前，用于模糊推理系統的學習算法主要是梯度下降算法和遞推最小二乘算法。梯度下降算法簡單易行、運算量小，但收斂速度慢，容易陷入局部極值，且對信號的譜性依賴較大;遞推最小二乘算法收斂速度很快，對信號譜性無依賴，但其結構復雜、運算量大且存在長期數值穩定的問題。從工程的角度考慮，因為非單點模糊推理系統的計算復雜度本身就較大，所以運算量大的遞推最小二乘算法不適合采用。為了彌補梯度下降算法的缺點，文中引入遺傳算法。遺傳算法是模擬生物進化過程的一種全局優化搜索算法，其目標函數既不要求連續，也不要求可微，僅要求問題可計算，而且它的搜索始終遍及整個解空間，容易得到全局最優解。用梯度下降算法和遺傳算法同時并行的搜索解空間，并定期交換信息。這樣不僅避免了陷入局部極值的缺點，而且加快了收斂速度。雖然由于遺傳算法的加入，運算量增加了，但由于遺傳算法和梯度下降算法并行工作，所以沒有降低算法的實時性。采用減法聚類的方法設置初始參數，進一步加快了算法的收斂速度。文中所設計的非單點模糊推理系統參數學習算法如下：

?

　　步驟1：設置初始參數。采用減法聚類算法對訓練數據[X，y]進行聚類處理，得M到個聚類中心

構造非單點模糊系統初始參數：選取聚類中心向量Xlc中的各個分量元素

作為式(2)中相應

的初始值;以

與最近的另一個聚類中心歐式距離的一半

作為式(2)中

作為式(2)中相應的初始值;已知訓練數據含有大量噪聲的情況下，取

?

　　步驟2：(1)采用梯度下降算法調整參數

(推導過程省略)。

?

?

　　(2)同時采用遺傳算法搜索最佳參數

　　1)對參數編碼。以減法聚類確定的初始參數值為參考，考慮參數的解空間在初始參數值的正負s倍范圍內，將解空間轉換為二進制，對各參數進行交叉組合編碼;

　　2)隨機生成20個個體作為初始群體;

　　3)將準則函數的數學期望E[φ(e(t))]映射為適應度函數

?

　　用該適應度函數對群體中個體的適應度進行評估，當適應度達到標準Ff,max時，進化停止;

　　4)遺傳操作：采用適應度比例方法進行選擇，兩點交叉方法進行交叉，采用基本變異算子進行變異。

　　步驟3：梯度下降算法和遺傳算法之間的信息交換。遺傳算法每進化q代，根據準則函數的數學期望E[φ(e(t))]比較遺傳算法和梯度下降算法所得參數的效果。若遺傳算法搜索到的參數更好，便用其作為梯度下降算法下一步運算的初始參數;若梯度下降算法得到的參數更好，便用其替代遺傳算法的當代群體中適應度最差的一個個體。

　　步驟4：當準則函數的數學期望E[φ(e(t))]達到標準1-Ff,max時，或者遺傳算法進化g代時，算法停止。文中用準則函數在訓練數據時間長度內的時間平均代替其數學期望進行運算。

　　3 基于NSFIS的制導炸彈智能控制系統的仿真設計

　　按照文獻[1]的設計思想，在仿真環境中采用NSFIS設計制導炸彈智能控制系統。

　　3.1 仿真環境的設定

　　假設以下的仿真環境：

　　(1)綜合風速UZ方向在水平面內，且為常矢;

　　(2)重力加速度為9.8 m/s2，無阻尼;

　　(3)彈翼可產生的最大調控加速度max a(t)(max a(t)=maxax(t)+maxay(t))隨下落高度增加，且不考慮彈翼產生的加速度a(t)在鉛垂方向的分量;

　　(4)高度H為7 075.4 m(即下落時間T為38 s)，按每0.25 s落下距離△h劃分高度空間為N=152層;

　　(5)轟炸方式為水平轟炸;

　　(6)控制過程不考慮時延;

　　(7)彈體運動為質點運動。

　　3.2 炸彈運動方程的分析

　　根據文獻[9，10]，水平轟炸的俯視圖，如圖1所示。

?

　　(oyxz)H：飛機航向坐標系;Of：飛機投彈點;Om：地面目標;A：無需調控，可直接命中彈D0在t時刻的坐標位置;A：需調控，方可命中彈D1在t時刻的坐標位置;B：需調控，方可命中彈D1在t-1時刻的坐標位置。

　　無需調控，可直接命中彈D0參數：Vx0：投彈點飛機空速;Uz0：投彈D0時的綜合風速;ε0：Vx0與Uz0的夾角;Xh(t)：t時刻彈在xH方向的坐標位置;Yh(t)：t時刻彈在yH方向的坐標位置。

　　需調控，方可命中彈D1參數：Vx1：投彈點飛機空速;Uz1：投彈D1時的綜合風速;ε1：Vx1與Uz1的夾角;Axe(t)：t時刻和t-1時刻彈在xH方向的位移差;Aye(t)：t時刻和t-1時刻彈在yH方向的位移差;Exh(t)：t時刻彈與目標Om的距離在xH方向的分量;Eyh(t)：t時刻彈與目標Om的距離在yH方向的分量;Vxh(t)：t時刻彈的速度在xH方向的分量;Vyh(t)：t時刻彈的速度在yH方向的分量。Axe(t)：t時刻彈D1和彈D0的位移差在xH方向的分量;Aye(t)：f時刻彈D1和彈D0的位移差在yH方向的分量。在仿真環境中，推導出彈D1在t時刻的運動方程

?

　　其中，Vax(t)為xH方向上t-1時刻加速度在時刻生成速度，Vay(t)為yH方向上t-1時刻加速度在t時刻生成速度。

　　3.3 制導炸彈智能控制系統的建立

　　根據彈道運動方程，x與y方向的控制相互獨立(a(t)=ax(t)+ay(t))，所以對空間每一層建立兩個非單點模糊子系統(NSFISix和NSFISiy)：NSFISix調控導彈在x方向的運動軌跡，輸入為Exh(t)、Axe(t)、Vxh(t)，輸出為ax(t);NSFISiy調控導彈在y方向的運動軌跡，輸入為Eyh(t)、Aye(t)、Vyh(t)，輸出為ay(t)。充分搜集每一層的訓練數據，利用文中提出的學習算法調整好NSFISix和NSFISiy的內部參數，就構成了基于NSFIS的制導炸彈智能控制系統，其概略流程圖，如圖2所示。

?

　　3.4 訓練數據的獲取

　　首先，采用如下算式解算a(t)

?

　　弧度，|Uz1|=28、29、30、31 m/s，|Vx1|=319、320、321、322 m/s，ε1=0.3、0.4、0.5、0.6弧度;通過調節參數cx、cy，得到64組圓概率誤差CEP∈(4，5)m的訓練數據，并對其加入一定程度的擾動誤差。

　　3.5 檢驗

　　設兩種投彈初始條件：

　　(a)|Uz1|=30 m/s，|Vx1|=321 m/s，ε1=0.5弧度(經訓練的投彈初始條件，即教師知識);

　　(b)|Uz1|=30.8 m/s，|Vx1|=319.7 m/s，ε1=0.38弧度(未經訓練的投彈初始條件，即非教師知識)。

　　用含有擾動誤差的訓練數據，對基于ANFIS的制導炸彈智能控制系統和基于NSFIS的制導炸彈智能控制系統分別進行訓練，并分別在(a)和(b)條件下進行投彈控制試驗。設得到兩種智能控制系統的控制結果比較如表1所示(表中數據為CEP，單位：m)。

?

　　從表1可以看出，無論在(a)還是(b)條件下，基于NSFIS的智能控制系統控制的命中精度都很高，而基于ANFIS的智能控制系統命中精度很低。這是因為ANFIS不具有抗噪聲能力，在訓練的過程中，將擾動也作為經驗進行了學習，因此其推理誤差必然較大，控制不準確。而NSFIS具有較強的抗噪聲能力，在學習過程中能夠去除擾動影響，因此其控制精度高。現實中，擾動是不可避免的，所以基于NSFIS的制導炸彈智能控制系統具有更高的工程應用價值。

　　4 結束語

　　試驗結果證明，在訓練數據含有噪聲的情況下，基于NSFIS的制導炸彈智能控制系統能夠自動濾除噪聲，實現高精度控制。這對制導炸彈智能控制系統的工程實現具有一定的意義。