在之前的濾波器教程中，我們研究了簡單的一階型低通和高通濾波器，它們的RC濾波器電路設計中只包含一個電阻器和一個無功元件（電容器）。

在使用濾波器對信號的頻譜進行整形的應用中，例如在通信或控制系統中，滾降的形狀或寬度也稱為“過渡帶”，對于簡單的一階濾波器，可能是太長或太寬，因此需要設計有多個“訂單”的有源濾波器。這些類型的過濾器通常稱為“高階”或“n th -order”過濾器。

復雜性或過濾器類型由過濾器“order”定義，這取決于其設計中的電容器或電感器等無功元件的數量。我們還知道，滾降率和過渡帶的寬度取決于濾波器的階數和簡單的一階濾波器，它具有20dB / decade或6dB的標準滾降率。 /octave.

然后，對于具有n th 數字順序的濾波器，它將具有20n dB / decade或6n dB / octave的后續滾降率。因此，一階濾波器的滾降率為20dB / decade（6dB /倍頻程），二階濾波器的滾降率為40dB / decade（12dB /倍頻程），四階濾波器具有滾降率為80dB / decade（24dB / octave）等等。

高階濾波器，例如三階，四階和五階通常是通過單個級聯在一起形成的 -

例如，兩個二階低通濾波器可以級聯在一起，產生一個四階低通濾波器，依此類推。盡管可以形成的濾波器的順序沒有限制，但隨著順序的增加，其尺寸和成本也會增加，其精度也會下降。

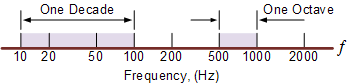
十年和八度

一個關于十年和 Octaves 的最終評論。在頻率范圍內，十年是十倍增加（乘以10）或十倍減少（除以10）。例如，2到20Hz代表十年，而50到5000Hz代表二十年（50到500Hz，然后是500到5000Hz）。

Octave是倍增（乘以2）或將頻率刻度減半（除以2）。例如，10到20Hz代表一個倍頻程，而2到16Hz是三個倍頻程（2到4,4到8，最后是8到16Hz），每次倍頻。無論哪種方式，對數標度在頻域中廣泛用于表示使用放大器和濾波器時的頻率值，因此了解它們非常重要。

對數頻率標度

h3>

由于頻率確定電阻器全部相等，并且頻率確定電容器，截止或角落也是如此第一，第二，第三或甚至四階濾波器的頻率（? C ）也必須相等，并使用我們現在熟悉的等式找到： / p>

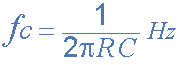
與一階和二階濾波器一樣，三階和四階高通濾波器由簡單地在等效低通濾波器中交換頻率確定部件（電阻器和電容器）的位置。可以按照我們之前在低通濾波器和高通濾波器教程中看到的步驟設計高階濾波器。但是，高階濾波器的總增益是固定的因為所有頻率確定分量都相等。

濾波器近似值

到目前為止，我們已經看過了低通和高通一階濾波器電路，它們產生的頻率和相位響應。一個理想的濾波器將為我們提供最大通帶增益和平坦度的規范，最小阻帶衰減以及阻止頻帶滾降（轉換頻帶）的非常陡峭的通帶，因此顯然會有大量的網絡響應滿足這些要求。

毫不奇怪，線性模擬濾波器設計中有許多“近似函數”，它們使用數學方法來最好地逼近濾波器設計所需的傳遞函數。

這種設計被稱為Elliptical，Butterworth，Chebyshev，Bessel，Cauer以及許多其他人。在這五個“經典”線性模擬濾波器近似函數中，只有Butterworth濾波器，尤其是低通巴特沃斯濾波器設計在這里被認為是最常用的函數。 / p>

低通巴特沃斯濾波器設計

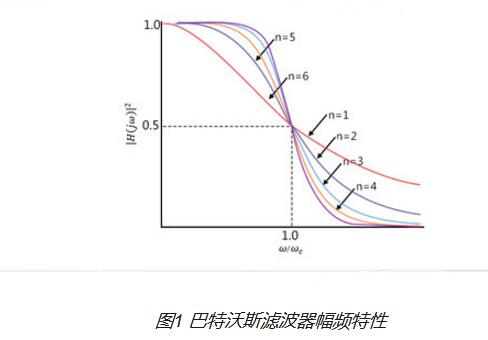
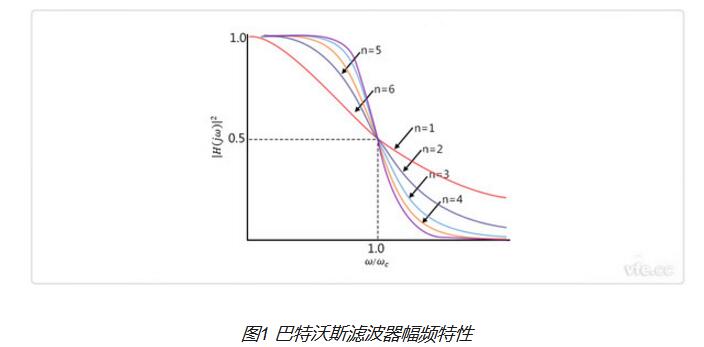
巴特沃斯濾波器近似函數的頻率響應通常也被稱為“最大平坦”（無波紋）響應，因為通帶設計為具有頻率響應，該頻率響應在數學上可以從0Hz（DC）變為平坦，直到-3dB的截止頻率沒有紋波。超過截止點的較高頻率在阻帶中以20dB / decade或6dB /倍頻程下降至零。這是因為它具有“質量因子”，“Q”僅為0.707。

然而，Butterworth濾波器的一個主要缺點是它以寬帶過渡帶為代價實現了這種通帶平坦度。當濾波器從通帶變為阻帶時。它的相位特性也很差。對于不同的濾波器階數，理想的頻率響應（稱為“磚墻”濾波器）和標準巴特沃斯近似值如下所示。

巴特沃斯濾波器的理想頻率響應

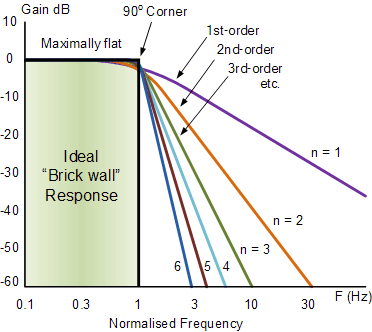
請注意，巴特沃斯濾波器階數越高，濾波器設計中的級聯級數越高，濾波器越接近理想的“磚墻”然而，在實踐中，Butterworth的理想頻率響應是無法實現的，因為它會產生過多的通帶紋波。

其中廣義方程表示“nth”訂購Butterworth濾波器，頻率響應如下：

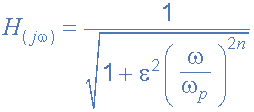
其中： n 表示濾波器順序，Omega ω等于2π?，Epsilon ε是最大通帶增益（A max ）。如果A max 的定義頻率等于截止-3dB角點（?c），則ε將等于1，因此ε 2 也將是一個。但是，如果您現在希望將A max 定義為不同的電壓增益值，例如1dB或1.1220（1dB = 20 * logA max ）則新值epsilon，ε可通過以下方式找到：

轉換等式給出：

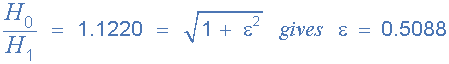
過濾器的頻率響應可以通過傳遞函數<在數學上定義/ b>標準電壓傳遞函數 H（jω）寫為：

注意：（jω）也可以寫成（s）來表示S域。和結果傳遞函數一秒鐘 - 階低通濾波器如下：

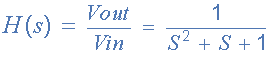
歸一化低通巴特沃斯濾波器多項式

幫助他的設計低通濾波器，Butterworth生成歸一化二階低通多項式的標準表，給出系數值對應于1弧度/秒的截止轉角頻率。

（1個+ S）（1 + 0.618s + S 2 ）（1 + 1.618s + S 2 ）

濾波器設計 - 巴特沃斯低通

查找有源低通巴特沃斯濾波器的順序其規格如下： A max = 0.5dB ，通帶頻率（ωp）為200弧度/秒（31.8Hz），在800弧度/秒的阻帶頻率（ωs）處， A min = -20dB 。還要設計合適的巴特沃斯濾波器電路以滿足這些要求。

首先，最大通帶增益 A max = 0.5dB 等于增益1.0593，記住：0.5dB = 20 * log（A），頻率（ωp）為200 rads / s，因此epsilon ε的值可通過以下方式找到：

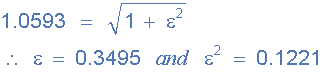
其次，最小阻帶增益A min = -20dB，等于增益（-20dB = 20 * log（A））在800 rads / s或127.3Hz的阻帶頻率（ωs）。

代替值為Butterworth濾波器頻率響應的一般方程給出了以下內容：

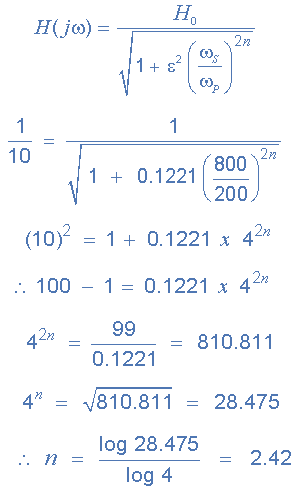
自 n 必須始終為整數（整數），然后下一個最高值為2.42 n = 3 ，因此需要“三階濾波器”并且要產生三階巴特沃茲濾波器，需要與一階濾波器級級聯的二階濾波器級。

從歸一化低通Butte上面的rworth多項式表，三階濾波器的系數給出為（1 + s）（1 + s + s 2 ），這給了我們一個增益 3-A = 1 ，或 A = 2 。當 A = 1 +（Rf / R1）時，為反饋電阻 Rf 和電阻 R1 選擇一個值會得到1kΩ和1kΩ分別為：（1kΩ/1kΩ）+ 1 = 2 。

我們知道截止角頻率，-3dB點（ω o ）可以使用公式 1 / CR 找到，但我們需要找到ω o 來自通帶頻率ω p 然后，

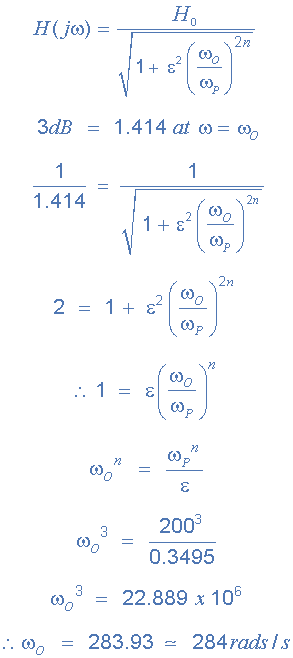
因此，截止轉角頻率為284 rads / s或45.2Hz，（284 /2π）并使用熟悉的公式 1 / CR 我們可以找到三階電路的電阻和電容值。

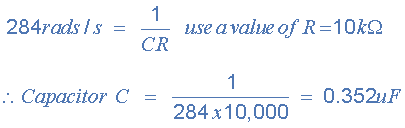
注意最接近的首選值為0.352 uF為0.36uF，或 360nF 。

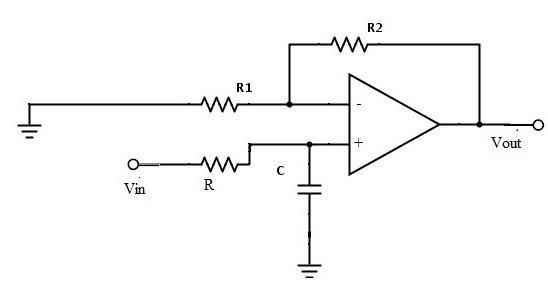
三階巴特沃斯低通濾波器

最后我們的三階低通電路巴特沃斯濾波器帶有截止角啁啾為284 rads / s或45.2Hz，最大通帶增益為0.5dB，最小阻帶增益為20dB，構造如下：

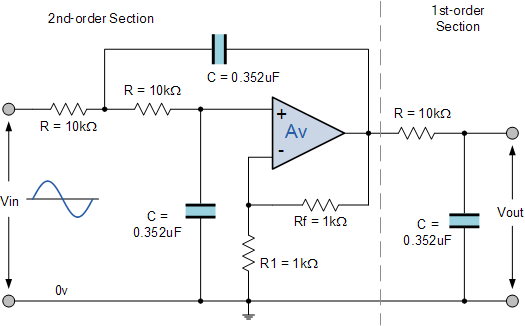
因此我們的三階巴特沃斯低通濾波器的轉折頻率為45.2Hz，C = 360nF且R =10kΩ