1 引言

在現代化戰場條件下，作戰平臺或用頻系統并不一定全部裝備有專業的頻譜監測設備，更多的是來源于作戰平臺或用頻系統自身的頻譜感知能力，因此，這些頻譜監測數據在時域、空域、頻域等多個維度上都是非常稀疏的甚至是非常匱乏的。需要對有限的、不連續的時空頻多維分布式頻譜監測進行數據匯集、融合，并對這些數據做頻譜推理預測，形成戰場復雜電磁環境的態勢信息，并形成可用頻譜資源的預測分析，從而為戰場頻譜管控提供依據。

頻譜推理技術是認知通信的重要基礎，其能夠通過模式挖掘、機器學習等方法為裝備系統提供在未知區域、未來時間或陌生頻譜的信道占用情況，在很大程度上提高了復雜電磁環境下的裝備生存適應能力，其在現代化戰爭中的意義不容忽視。

頻譜推理是基于歷史已知頻譜數據來挖掘數據內在的相關性或者規律性，以獲得將來未知無線頻譜的數據狀態[1]。頻譜推理也是一把雙刃劍，一方面它能夠通過歷史數據來預測信道未來某一段時間內的信道狀態，提供非授權用戶的吞吐量，能夠縮短感知時間在自適應頻譜感知中的能量消耗；另一方面，它也會不可避免地帶來預測虛警和預測漏檢[2-3]。

現有的頻譜推理技術主要關注于一維的時間維度，而頻率和空間維度上的推理技術則極少涉及，G?Ding等[4]驗證了頻譜狀態的可預測性。對于時間維度頻譜推理，隱馬爾可夫模型（Hidden Markov Model，HMM）推理法和神經網絡（Neural Network，NN）方法具有較好的推理精度，然而關于這兩種方法的研究大多局限于下一時隙的占用情況推理，這與現實應用場景還有很大的差距。此外，隱馬爾科夫模型推理法[5]的推理準確度受限于所用轉換矩陣的階數，越復雜的場景，模型所需的階數越高，其中隱含的狀態規律越難以描述，而且模型運算的復雜度會呈指數關系上升，因而，HMM模型并不適用于復雜的頻譜推理場景。相對而言，NN算法[6]能夠通過神經元的作用模擬應用場景中存在的非線性轉化關系，并通過離線學習得到網絡中節點間的權重值，對于更復雜的電磁頻譜環境，可以增加神經網絡的隱藏層數量[7]和各層的神經元數量[8]等。因而，NN算法相對于HMM算法更適用于多維度復雜電磁頻譜推理場景。

鑒于頻譜在空間和頻率維度上的關聯特性，NN算法可分別用于一維空間和一維頻率維度頻譜推理。本研究結合NN算法的優缺點，提出一種適用于時間維度多時隙頻譜的推理算法——LSTM（Long Short Term Memory）算法，并以此為基礎，分別設計可用于時頻二維頻譜推理以及時空頻三維的頻譜推理方法，后者可以完全移植到網格結構的應用場景中。目前，多維頻譜推理技術尚處于初步探索研究階段，還沒有形成較為完善的理論體系，也缺少實際應用場景驗證。

2 長短時記憶網絡（LSTM）推理法

相關研究證明，信道狀態具有高度的自相關特性，且伴隨著不同的時移，相關性呈現逐漸下降的趨勢。LSTM推理法在時間或者空間序列數據的處理上具備較大的優勢[9]。LSTM網絡單元結構如圖1所示：

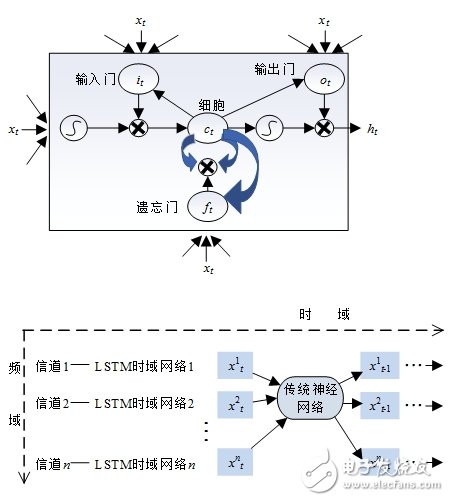
圖1 LSTM網絡單元結構

長短時記憶網絡LSTM克服了RNN（Recurrent Neural Networks）網絡訓練過程中無法快速收斂的缺點[10]，其通過引入三個門單元（輸入門、遺忘門、輸出門）來合理地控制歷史與現在信息之間的關系，如圖1所示，LSTM主要涉及的公式如下：

it=σ(Wxixt+Whiht-1+Wcict-1+bi) (1)

ft=σ(Wxfxt+Whfht-1+Wcfct-1+bf) (2)

ct=ft⊙ct-1+it⊙tanh(Wxcixt+Whcht-1+bc) (3)

ot=σ(Wxoxt+Whoht-1+Wcoct+bo) (4)

ht=ot⊙tanh(ct) (5)

其中，σ為邏輯S型函數，i、f、o、c為相應的輸入門、遺忘門、輸出門和記憶細胞激活向量，⊙表示向量間對應元素相乘，W(..)代表相應的各個權重矩陣，其中從細胞到各個門的矩陣為對角陣，而其余的各權重矩陣為非對角陣。

與一維時間序列頻譜推理相匹配的LSTM網絡結構如圖2所示，基于LSTM網絡的頻譜推理方法可以靈活地調整推理網絡結構，進而可以在推理不同時隙長度的應用中進行切換。與此同時，該方法的另外一個優勢是，普通的推理算法（HMM或NN等）只能夠對共享信道的可用性與否（即0-1值）進行推理判定，而LSTM方法還可以對信道的能量水平進行推理，從而極大地增加了認知設備在接入信道過程中設計接入判定準則時的靈活性，進一步提升了接入信道的效率，并降低了認知設備的感知能量消耗水平。

圖2 一維時間序列推理LSTM網絡結構示意圖

3 時頻二維頻譜推理法（2D混合網絡）

基于多種網絡算法的結合算法能夠通過不同網絡的特長優勢匹配而達到更為滿意的處理或推理效果，因此，混合神經網絡在頻譜推理領域的應用前景巨大。多項研究分析表明，頻譜的使用情況在頻域上也存在很大的相關性，這里提出了一種LSTM網絡與神經網絡結合的適用于時頻二維頻譜推理的算法，算法中的網絡關系如圖3所示：

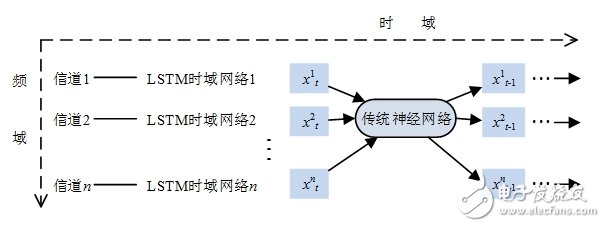
圖3 時頻二維頻譜推理網絡關系圖

該混合網絡主要基于時頻域頻譜所具有的相關性而構建。LSTM通過遺忘門表達出歷史感知數據對未來推理數據的潛在影響關系。在無神經網絡加入時，頻譜推理的過程實現多條并行的時間序列推理功能，且相互之間無關聯，而在神經網絡與LSTM網絡結合之后，混合網絡既能用于推理其中一條或多條未知信道的占用情況，也可以推理整個信道所占頻域的下一時隙（或多時隙）的使用情況。

用于時頻域頻譜推理的混合神經網絡參數結構如圖4所示，圖4只描述了時隙t時的頻譜推理過程，從圖4可以看出，不同信道的LSTM結構是獨立的平行關系，在此基礎上，時隙t得出的各信道輸出被當做輸入值傳輸到MLP推理器中，經過該推理器處理后，得出下一時隙（t+1）或繼續輸入得到未來多個時隙的各信道占用情況。由于LSTM與神經網絡相對明確的連接關系，在訓練過程中，混合網絡的后向傳播過程基本等價于原來二者訓練方式的加和，因而該混合網絡并沒有明顯增加訓練的復雜度，在一定的針對性訓練操作之后，各前向權重矩陣和偏差值收斂到穩定值，繼而可以用于后續的二維頻譜推理過程。

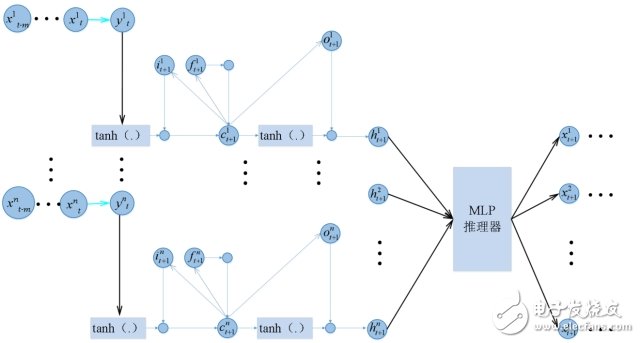
圖4 時頻二維頻譜推理網絡參數關系示意圖

4 時空頻三維頻譜推理法（3D混合網絡）

在LSTM算法和時頻頻譜推理算法的基礎上，提出一種適用于網格結構的時空頻頻譜推理算法。在網格結構的頻譜推理中，已知多個不同空間節點在時間和頻率維度上的頻譜感知信息，需運算推測出未知空間位置的頻譜占用情況（或功率水平），提出能夠滿足該需求的推理算法網絡結構如圖5所示：

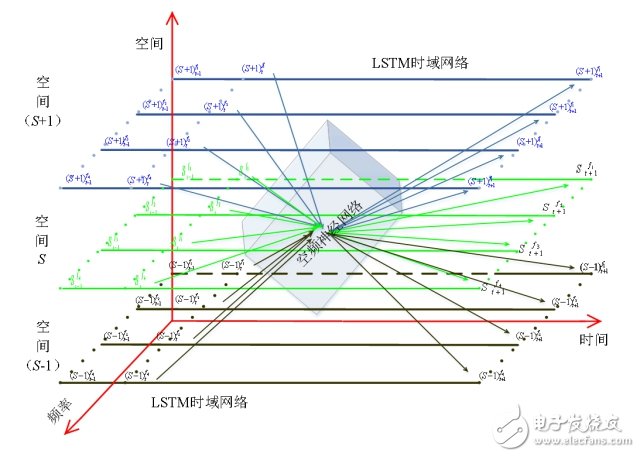
圖5 時空頻三維頻譜推理網絡示意圖

在該網絡結構中，時間維度使用LSTM基礎網絡，頻率和空間維度使用神經網絡。其中，未知節點位于空間S，而（S-1）與（S+1）等空間節點的頻譜使用情況是已知信息，在網絡的訓練過程中，多個空間（不限于圖中給出的三個）的歷史信息作為輸入信息，而輸出可以根據實際需求進行調整，若僅需要空間S的未來頻譜使用情況，則可以僅以作為輸出。同時，各權重關系可以通過適當的刪減來匹配實際中的影響關系，同時降低權重反向迭代過程中具備的運算壓力。

在該3D神經網絡中，傳統神經網絡結構可以進行適當的改進或者直接被替換成推理效果更好的卷積神經網絡（CNN，Convolutional Neural Networks）等結構。可以看出，該3D神經網絡結合了空間頻譜的相對關系，能夠通過調整網絡中的連接關系以適用于時空頻多維頻譜數據。具體來說，該立體結構混合神經網絡能夠推理點（信道時隙點）、線（單信道或單一時隙或不同空間時隙點）、面（多信道時隙或多信道空間或多時隙空間）、體（信道時隙空間）結構的頻譜占用情況。

5 頻譜推理技術比較

已有頻譜推理算法與當前提出的各頻譜推理算法的參數與性能對比如表1所示：

傳統的隱馬爾可夫模型算法不適用于復雜場景；神經網絡算法可適用于復雜場景，但訓練較慢；長短時記憶網絡推理法適用于復雜場景下的序列關系，且訓練較快；時頻二維頻譜推理法適用于二維關系場景，訓練速度可通過與基因算法結合來改進；時空頻三維頻譜推理法適用于三維關系場景，訓練速度可通過與基因算法結合來改進，網絡結構也可進一步優化。

6 結束語

本文提出的適用于時間維度多時隙頻譜的推理、時頻二維頻譜推理以及時空頻三維的頻譜推理方法能夠在有限的、不連續的時空頻多維頻譜監測數據情況下實現頻譜推理預測，從而為戰場頻譜管控提供支撐。該研究目前處于仿真試驗階段，其有效性尚待驗證。