LQR （線性二次調(diào)解器）理論是現(xiàn)代控制理論中發(fā)展最早也最為成熟的一種狀態(tài)空間設(shè)計(jì)法。特別可貴的是，LQR可得到狀態(tài)線性反饋的最優(yōu)控制規(guī)律，易于構(gòu)成閉環(huán)最優(yōu)控制。

LQR 最優(yōu)設(shè)計(jì)是指設(shè)計(jì)出的狀態(tài)反饋控制器 K 要使二次型目標(biāo)函數(shù) J 取最小值，而 K 由權(quán)矩陣 Q 與 R 唯一決定，故此 Q、R 的選擇尤為重要。

MPC（模型預(yù)測(cè)控制）是一種先進(jìn)的過程控制方法，在滿足一定約束條件的前提下，被用來(lái)實(shí)現(xiàn)過程控制，它的實(shí)現(xiàn)依賴于過程的動(dòng)態(tài)模型（通常為線性模型）。

在控制時(shí)域（一段有限時(shí)間）內(nèi)，它主要針對(duì)當(dāng)前時(shí)刻進(jìn)行優(yōu)化，但也考慮未來(lái)時(shí)刻，求取當(dāng)前時(shí)刻的最優(yōu)控制解，然后反復(fù)優(yōu)化，從而實(shí)現(xiàn)整個(gè)時(shí)域的優(yōu)化求解。

本文由社區(qū)開發(fā)者——呂伊鵬撰寫，對(duì)MPC與LQR進(jìn)行了較為詳細(xì)的比較，希望這篇文給感興趣的同學(xué)帶來(lái)更多幫助。

Apollo中用到了PID、MPC和LQR三種控制器，其中，MPC和LQR控制器在狀態(tài)方程的形式、狀態(tài)變量的形式、目標(biāo)函數(shù)的形式等有諸多相似之處，因此結(jié)合自己目前了解到的信息，將兩者進(jìn)行一定的比較。

MPC(Model Predictive Control，模型預(yù)測(cè)控制)和LQR(Linear–Quadratic Regulator，線性二次調(diào)解器) 在狀態(tài)方程、控制實(shí)現(xiàn)等方面，有很多相似之處，但也有很多不同之處，如工作時(shí)域、最優(yōu)解等，基于各自的理論基礎(chǔ)，從研究對(duì)象、狀態(tài)方程、目標(biāo)函數(shù)、求解方法等方面，對(duì)MPC和LQR做簡(jiǎn)要對(duì)比分析。

本文主要參考內(nèi)容：

【1】龔建偉,姜巖,徐威.無(wú)人駕駛車輛模型預(yù)測(cè)控制[M].北京理工大學(xué)出版社, 2014.

【2】Model predictive control-Wikipedia.

【3】Linear–quadratic regulator-Wikipedia.

【4】Inverted Pendulum: State-Space Methods for Controller Design.

【5】王金城. 現(xiàn)代控制理論[M]. 化學(xué)工業(yè)出版社, 2007。

LQR的研究對(duì)象是現(xiàn)代控制理論中以狀態(tài)空間方程形式給出的線性系統(tǒng)。MPC的研究對(duì)象可以是線性系統(tǒng)，也可以是非線性系統(tǒng)，只不過為了某些需求，如時(shí)效性，計(jì)算的便捷，操控性等，一般會(huì)將非線性系統(tǒng)轉(zhuǎn)換為線性系統(tǒng)進(jìn)行計(jì)算。非線性系統(tǒng)的線性化可參考上一篇文章。

Apollo中，LQR和MPC控制器都選用的單車動(dòng)力學(xué)模型作為研究對(duì)象，單車動(dòng)力學(xué)模型為非線性系統(tǒng)，但LQR和MPC控制器的目的是為了求最優(yōu)控制解，在具體的優(yōu)化求解時(shí)，均通過線性化方法將狀態(tài)方程轉(zhuǎn)化為線性方程進(jìn)行求解，所以，可以說(shuō)Apollo中LQR和MPC控制器的研究對(duì)象均為線性系統(tǒng)。

LQR的狀態(tài)方程多以微分方程的形式給出，如：

是一個(gè)連續(xù)線性系統(tǒng)，在計(jì)算過程中需要轉(zhuǎn)換為如公式3的離散線性系統(tǒng)。

MPC的狀態(tài)方程可以為線性系統(tǒng)，可以為非線性系統(tǒng)，非線性系統(tǒng)形如下：

線性系統(tǒng)如公式3所示：

但LQR和MPC在計(jì)算求解時(shí)基本都是基于離散線性方程計(jì)算的。公式1可以很方便的轉(zhuǎn)化為公式3的形式。

按照維基百科的說(shuō)法：

LQR在一個(gè)固定的時(shí)域上求解，且一個(gè)時(shí)域內(nèi)只有一個(gè)最優(yōu)解，而MPC在一個(gè)逐漸消減的時(shí)域內(nèi)(in a receding time window)求解最優(yōu)解，且最優(yōu)解經(jīng)常更新。

可以結(jié)合MPC的滾動(dòng)優(yōu)化，以及圖1進(jìn)行理解：

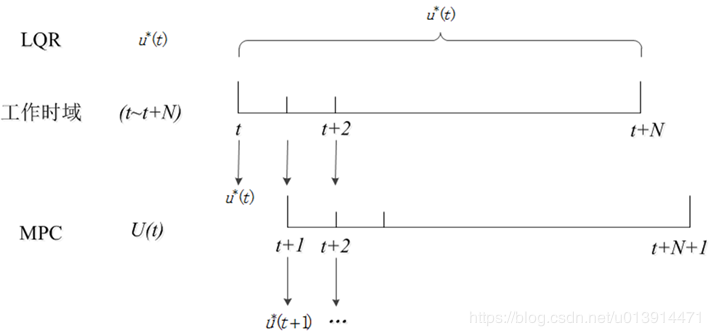
圖1 MPC和LQR的工作時(shí)域

針對(duì)同一工作時(shí)域[t,t+N]，LQR在該時(shí)域中，有唯一最優(yōu)控制解u?(t)，而MPC僅在t時(shí)刻有最優(yōu)解u?(t)，但它會(huì)計(jì)算出一個(gè)控制序列U(t) ，并僅將序列的第一個(gè)值u?(t)作為控制量輸出給控制系統(tǒng)，然后在下一采樣時(shí)間結(jié)合車輛當(dāng)前狀況求取下一個(gè)最優(yōu)控制解u?(t+1)，這就是MPC所謂的滾動(dòng)優(yōu)化。

這么做的目的是為了使控制效果在一定時(shí)間內(nèi)可期，并且能根據(jù)控制效果盡早調(diào)整控制變量，使實(shí)際狀態(tài)更切合期望狀態(tài)。

此外，LQR的工作時(shí)域可以拓展到無(wú)限大，即可以求取無(wú)限時(shí)域的最優(yōu)控制解。而MPC只針對(duì)有限時(shí)域。

優(yōu)化求解問題一般離不開目標(biāo)函數(shù)的設(shè)計(jì)。

LQR的目標(biāo)函數(shù)的一般形式為：

其中，終端狀態(tài)，

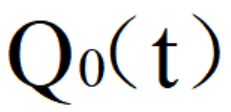
正定的終端加權(quán)矩陣，x為狀態(tài)變量，多為各種誤差，u為控制變量，Q為半正定的狀態(tài)加權(quán)矩陣，R為正定的控制加權(quán)矩陣，實(shí)際應(yīng)用中，Q、R多為對(duì)角矩陣。

MPC的目標(biāo)函數(shù)的一般形式為：

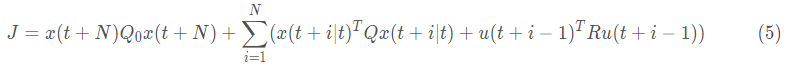
其中，

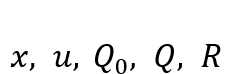
從形式上可以看出，LQR的目標(biāo)函數(shù)為積分形式，MPC的目標(biāo)函數(shù)為求和形式，但其實(shí)都是對(duì)代價(jià)的累計(jì)。

兩者第一部分均為終端代價(jià)函數(shù)，當(dāng)系統(tǒng)對(duì)終端狀態(tài)要求極嚴(yán)的情況下才添加，一般情況下可省略。

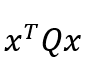跟蹤代價(jià)，表示跟蹤過程中誤差的大小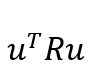，控制代價(jià)，表示對(duì)控制的約束或要求等。

正如工作時(shí)域所述，針對(duì)同一工作時(shí)域，LQR有唯一最優(yōu)控制解，也就是在該控制周期內(nèi)，LQR只進(jìn)行一次計(jì)算。

而MPC滾動(dòng)優(yōu)化的思想，使其給出該時(shí)域內(nèi)的一組控制序列對(duì)應(yīng)不同的采樣時(shí)刻（采樣周期和控制周期不一定相同），但是只將該序列的第一個(gè)值輸出給被控系統(tǒng)，作為該時(shí)刻的最優(yōu)控制解。

因此，對(duì)于工作時(shí)域[t,t+N]，LQR只有唯一解，對(duì)于線性MPC，本質(zhì)是凸優(yōu)化問題，只有唯一解；但非線性MPC，可能會(huì)有N個(gè)local optimal。

最優(yōu)控制解的求取多基于目標(biāo)函數(shù)進(jìn)行，取線性約束下的目標(biāo)函數(shù)的極值為最優(yōu)控制解。對(duì)于系統(tǒng)為線性，目標(biāo)函數(shù)為狀態(tài)變量和控制變量的二次型函數(shù)的線性二次性問題，最優(yōu)解具有統(tǒng)一的解析表達(dá)式。

Apollo中的MPC將優(yōu)化問題轉(zhuǎn)化為二次規(guī)劃問題，利用二次規(guī)劃求解器進(jìn)行求解。橫向控制中用的是LQR調(diào)節(jié)器，它通過假設(shè)控制量u(t)不受約束，利用變分法求解。

此外，LQR對(duì)整個(gè)時(shí)域進(jìn)行優(yōu)化求解，且求解過程中假設(shè)控制量不受約束，但是實(shí)際情況下，控制量是有約束的。

而MPC通常在比整個(gè)時(shí)域更小的時(shí)間窗口中解決優(yōu)化問題，因此可能獲得次優(yōu)解，且對(duì)線性不作任何假設(shè)，它能夠處理硬約束以及非線性系統(tǒng)偏離其線性化工作點(diǎn)的遷移，這兩者都是MPC的缺點(diǎn)。