TensorFlow 不僅僅可以用于機器學習。在此教程中,我們所舉的例子(較為尋常)是使用 TensorFlow 模擬偏微分方程的行為(https://en.wikipedia.org/wiki/Partial_differential_equation)。我們將模擬幾個雨滴落在方形池塘水面的情形。
基本設置
需要導入一些庫。
#Import libraries for simulationimport tensorflow as tfimport numpy as np#Imports for visualizationimport PIL.Imagefrom io import BytesIOfrom IPython.display import clear_output, Image, display
將池塘水面的狀態顯示為圖像的函數。
def DisplayArray(a, fmt='jpeg', rng=[0,1]): """Display an array as a picture.""" a = (a - rng[0])/float(rng[1] - rng[0])*255 a = np.uint8(np.clip(a, 0, 255)) f = BytesIO() PIL.Image.fromarray(a).save(f, fmt) clear_output(wait = True) display(Image(data=f.getvalue()))
接下來,我們發起一個互動式 TensorFlow 會話,以方便練習。如果我們使用可執行的 .py 文件進行模擬,則常規會話一樣可行。
sess = tf.InteractiveSession()
計算便利函數
def make_kernel(a):
"""Transform a 2D array into a convolution kernel""" a = np.asarray(a) a = a.reshape(list(a.shape) + [1,1]) return tf.constant(a, dtype=1)def simple_conv(x, k): """A simplified 2D convolution operation""" x = tf.expand_dims(tf.expand_dims(x, 0), -1) y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding='SAME') return y[0, :, :, 0]def laplace(x): """Compute the 2D laplacian of an array""" laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]]) return simple_conv(x, laplace_k)
定義 PDE
我們的池塘是一個完美的 500 x 500 正方形,就像自然界中的大多數池塘一樣。
N = 500
接下來,我們創建池塘,并在其表面落入一些雨滴。
# Initial Conditions -- some rain drops hit a pond
# Set everything to zerou_init = np.zeros([N, N], dtype=np.float32)ut_init = np.zeros([N, N], dtype=np.float32)# Some rain drops hit a pond at random pointsfor n in range(40): a,b = np.random.randint(0, N, 2) u_init[a,b] = np.random.uniform()DisplayArray(u_init, rng=[-0.1, 0.1])
現在,我們指定微分方程的詳細信息。
# eps -- time resolution# damping -- wave dampingeps = tf.placeholder(tf.float32, shape=())damping = tf.placeholder(tf.float32, shape=())# Create variables for simulation stateU = tf.Variable(u_init)Ut = tf.Variable(ut_init)# Discretized PDE update rulesU_ = U + eps * UtUt_ = Ut + eps * (laplace(U) - damping * Ut)# Operation to update the statestep = tf.group( U.assign(U_), Ut.assign(Ut_))
運行模擬
情況變得有趣起來 - 使用簡單的 for 循環讓其持續運行。
# Initialize state to initial conditions
tf.global_variables_initializer().run()# Run 1000 steps of PDEfor i in range(1000): # Step simulation step.run({eps: 0.03, damping: 0.04}) DisplayArray(U.eval(), rng=[-0.1, 0.1])
-
機器學習
+關注
關注
66文章
8438瀏覽量
133086 -
tensorflow
+關注
關注
13文章
329瀏覽量
60631
原文標題:TensorFlow 不僅用于機器學習,還能模擬偏微分方程
文章出處:【微信號:tensorflowers,微信公眾號:Tensorflowers】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Matlab偏微分方程工具箱應用說明
Matlab求解微分方程(ODEs/PDEs)
計算機Fortran編程實現偏微分方程拉普拉斯變換
偏微分方程式數值解之計算機算法詳解
偏微分方程式數值解之計算機Fortran算法詳解附圖(續i)
偏微分方程式數值解之計算機Fortran算法詳解附圖(續ii)
常微分方程的MAtLAB解法
微分方程式的建立與求解
基于偏微分方程的閃光照相圖像修補算法
基于分數階偏微分方程在圖像處理中應用設計
異性四階偏微分方程耦合二階偏微分方程的圖像放大算法
模擬集成電路之頻率響應分析零極點
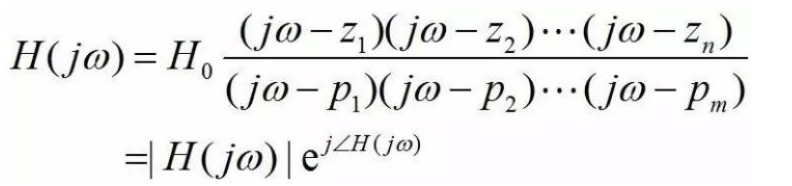
Matlab/Simulink建模詳解:一階時變偏微分方程的求解
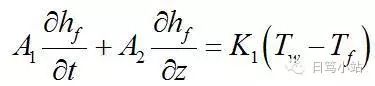




 TensorFlow在機器學習和模擬偏微分方程中的應用
TensorFlow在機器學習和模擬偏微分方程中的應用










評論