前言
支持向量機是一種經典的機器學習算法,在小樣本數據集的情況下有非常廣的應用,我覺得,不懂支持向量機不算是入門機器學習。本篇循序漸進的講解了支持向量機的分類思想,希望對您有幫助。
目錄
1. 函數間隔和幾何間隔
2. 支持向量機的分類思想
3. 總結
1. 函數間隔和幾何間隔
為了能夠更好的闡述支持向量機的分類思想,需要理解函數間隔和幾何間隔的定義。
1. 點到超平面的距離
假設超平面方程:
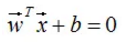
點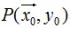 到平面的距離:
到平面的距離:
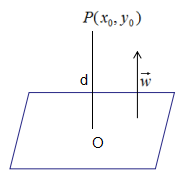
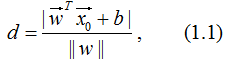
由上式可得: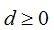 沒有分類信息,而函數間隔和幾何間隔不僅包含了距離信息,還包含了分類信息。
沒有分類信息,而函數間隔和幾何間隔不僅包含了距離信息,還包含了分類信息。
2. 函數間隔和幾何間隔
對于給定的訓練數據集T,正樣本和負樣本分別為+1和-1,我們對式(1.1)稍微進行了修改:
(1). 點到平面的距離不作規范化處理,得:
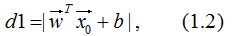
(2). 去掉絕對值符號,并乘以標記結果y0,得:
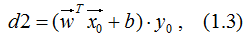
d2表達式就是函數間隔的定義,有兩層含義:大小表示點P0到超平面的距離,正負表示點P0是否正確分類,若d<0,分類錯誤;反之,則分類正確。
因此,我們定義點到超平面的函數間隔為:
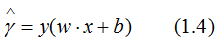
接著定義訓練數據集T的函數間隔是所有樣本點(xi,yi)的函數間隔的最小值,即:
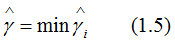
其中,
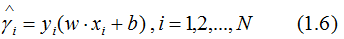
但是,若成比例的增加超平面參數w和b,超平面沒有改變,但是函數間隔卻成比例的增加了,這是不符合理論的,因此,需要對函數間隔進行規范化,得:
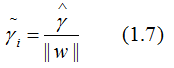
(1.7)式就是幾何間隔的定義,幾何間隔的值是確定的。
2. 支持向量機的分類思想
1. 感知機和logistic回歸的分類思想
感知機的損失函數為所有誤分類點到超平面的距離之和:
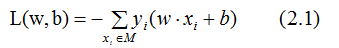
無誤分類點時,損失函數為0,滿足模型分類條件的超平面有無數個,如下圖:
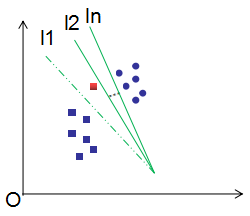
初始超平面為l1,誤分類點為紅色框,最小化式(2.1)有無窮多個滿足損失函數為0的超平面,如上圖的l2~ln,然而,最佳分類超平面只有一個,即支持向量機所對應的超平面。
假設logistic回歸的模型是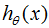 ,logistic回歸的損失函數:
,logistic回歸的損失函數:
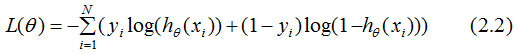
簡單分析(2.2)式的分類思想:
(1).當yi=1時,損失函數簡化為:
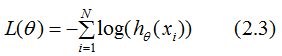
若要使損失函數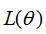 越小越好,則xi的值越大越好,如下圖:
越小越好,則xi的值越大越好,如下圖:
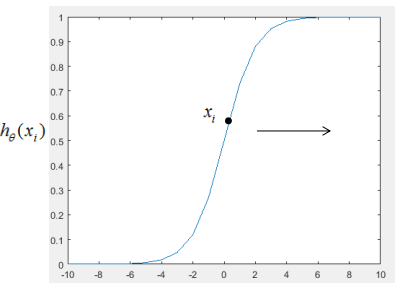
圖2.1
當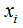 往箭頭方向移動時,損失函數
往箭頭方向移動時,損失函數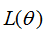 逐漸變小。
逐漸變小。
(2). 當yi=0時,損失函數簡化為:
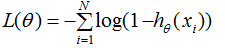
若要使損失函數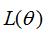 越小越好,則xi的值越小越好,如下圖:
越小越好,則xi的值越小越好,如下圖:
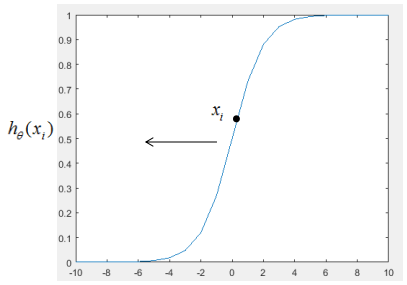
當往箭頭方向移動時,損失函數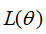 逐漸變小。
逐漸變小。
2. 支持向量機的分類思想
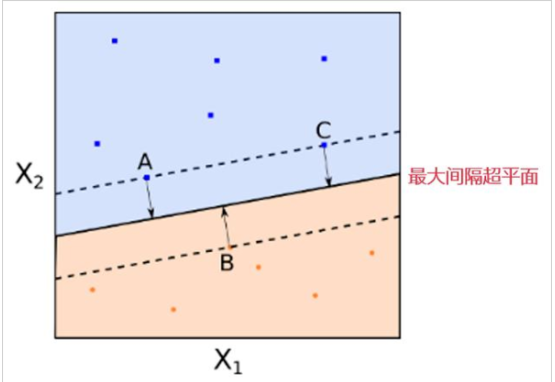
支持向量機結合了感知機和logistic回歸分類思想,假設訓練樣本點(xi,yi)到超平面H的幾何間隔為γ(γ>0),由上節定義可知,幾何間隔是點到超平面最短的距離,如下圖的紅色直線:
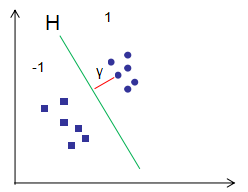
用logisitic回歸模型分析幾何間隔:
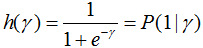
因此,當γ越大時,損失函數越小,結果為正樣本的概率也越大。
因此,感知機的分類思想是最大化點到超平面的幾何間隔,這個問題可以表示為下面的約束最優化問題:
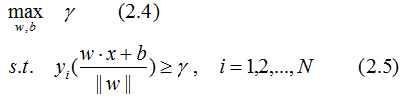
根據幾何間隔和函數間隔的關系,得幾何間隔的約束最優化問題:
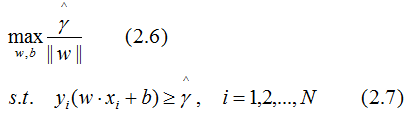
函數間隔是樣本點到超平面的最短距離,因此,令函數間隔為常數1,那么其他樣本點到超平面的距離都大于1,且最大化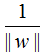 和最小化
和最小化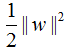 是等價的。于是就得到下面的最優化問題:
是等價的。于是就得到下面的最優化問題:
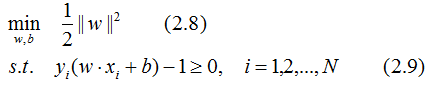
由(2.8)式和(2.9)式,解得最優解w*,b*,易知最優超平面到正負樣本的幾何間隔相等(請理解幾何間隔的含義,然后仔細回想整個分類過程,就會得到這個結論)。
3. 總結
本文結合了感知機和logistic回歸的分類思想來推導支持向量機的最優化問題,即最大間隔分離超平面。
-
函數
+關注
關注
3文章
4346瀏覽量
62971 -
機器學習
+關注
關注
66文章
8438瀏覽量
133084
原文標題:支持向量機(一):支持向量機的分類思想
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
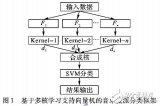
基于多分類支持向量機的隱寫域盲檢測
多分類孿生支持向量機研究進展
多核學習支持向量機應用音樂流派自動分類
什么是支持向量機 什么是支持向量




 支持向量機的分類思想
支持向量機的分類思想










評論