引言

CTR問題我們有兩種角度去理解，一種是分類的角度，即將點擊和未點擊作為兩種類別。另一種是回歸的角度，將點擊和未點擊作為回歸的值。不管是分類問題還是回歸問題，一般在預估的時候都是得到一個[0,1]之間的概率值，代表點擊的可能性的大小。

如果將CTR預估問題當作回歸問題，我們經常使用的損失函數是MSE；如果當作二分類問題，我們經常使用的損失函數是LogLoss。而對于一個訓練好的模型，我們往往需要評估一下模型的效果，或者說泛化能力，MSE和LogLoss當然也可以作為我們的評價指標，但除此之外，我們最常用的還是AUC。

想到這里，我想到一個問題，AUC是否可以直接用作損失函數去優化呢？

說了這么多，我們還不知道AUC是什么呢？不著急，我們從二分類的評估指標慢慢說起，提醒一下，本文二分類的類別均為0和1，1代表正例，0代表負例。

1、從二分類評估指標說起

1.1 混淆矩陣

我們首先來看一下混淆矩陣，對于二分類問題，真實的樣本標簽有兩類，我們學習器預測的類別有兩類，那么根據二者的類別組合可以劃分為四組，如下表所示：

上表即為混淆矩陣，其中，行表示預測的label值，列表示真實label值。TP，FP，FN，TN分別表示如下意思：

TP（true positive）：表示樣本的真實類別為正，最后預測得到的結果也為正；FP（false positive）：表示樣本的真實類別為負，最后預測得到的結果卻為正；FN（false negative）：表示樣本的真實類別為正，最后預測得到的結果卻為負；TN（true negative）：表示樣本的真實類別為負，最后預測得到的結果也為負.

可以看到，TP和TN是我們預測準確的樣本，而FP和FN為我們預測錯誤的樣本。

1.2 準確率Accruacy

準確率表示的是分類正確的樣本數占樣本總數的比例，假設我們預測了10條樣本，有8條的預測正確，那么準確率即為80%。

用混淆矩陣計算的話，準確率可以表示為：

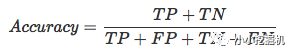
雖然準確率可以在一定程度上評價我們的分類器的性能，不過對于二分類問題或者說CTR預估問題，樣本是極其不平衡的。對于大數據集來說，標簽為1的正樣本數據往往不足10%，那么如果分類器將所有樣本判別為負樣本，那么仍然可以達到90%以上的分類準確率，但這個分類器的性能顯然是非常差的。

1.3 精確率Precision和召回率Recall

為了衡量分類器對正樣本的預測能力，我們引入了精確率Precision和召回率Recall。

精確率表示預測結果中，預測為正樣本的樣本中，正確預測為正樣本的概率；召回率表示在原始樣本的正樣本中，最后被正確預測為正樣本的概率；

二者用混淆矩陣計算如下：

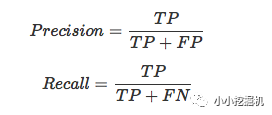
精確率和召回率往往是一對矛盾的指標。在CTR預估問題中，預測結果往往表示會被點擊的概率。如果我們對所有的預測結果進行降序排序，排在前面的是學習器認為最可能被點擊的樣本，排在后面的是學習期認為最不可能被點擊的樣本。

如果我們設定一個閾值，在這個閾值之上的學習器認為是正樣本，閾值之下的學習器認為是負樣本。可以想象到的是，當閾值很高時，預測為正樣本的是分類器最有把握的一批樣本，此時精確率往往很高，但是召回率一般較低。相反，當閾值很低時，分類器把很多拿不準的樣本都預測為了正樣本，此時召回率很高，但是精確率卻往往偏低。

1.4 F-1 Score

為了折中精確率和召回率的結果，我們又引入了F-1 Score，計算公式如下：

對于F1 Score有很多的變化形式，感興趣的話大家可以參考一下周志華老師的西瓜書，我們這里就不再介紹了。

1.5 ROC與AUC

在許多分類學習器中，產生的是一個概率預測值，然后將這個概率預測值與一個提前設定好的分類閾值進行比較，大于該閾值則認為是正例，小于該閾值則認為是負例。如果對所有的排序結果按照概率值進行降序排序，那么閾值可以將結果截斷為兩部分，前面的認為是正例，后面的認為是負例。

我們可以根據實際任務的需要選取不同的閾值。如果重視精確率，我們可以設定一個很高的閾值，如果更重視召回率，可以設定一個很低的閾值。

到這里，我們會拋出兩個問題：1)設定閾值然后再來計算精確率，召回率和F1-Score太麻煩了，這個閾值到底該設定為多少呢？有沒有可以不設定閾值來直接評價我們的模型性能的方法呢？

2)排序結果很重要呀，不管預測值是多少，只要正例的預測概率都大于負例的就好了呀。

沒錯，ROC和AUC便可以解決我們上面拋出的兩個問題。

ROC全稱是“受試者工作特征”，（receiver operating characteristic）。我們根據學習器的預測結果進行排序，然后按此順序逐個把樣本作為正例進行預測，每次計算出兩個重要的值，分別以這兩個值作為橫縱坐標作圖，就得到了ROC曲線。

這兩個指標是什么呢？是精確率和召回率么？并不是的，哈哈。

ROC曲線的橫軸為“假正例率”（True Positive Rate,TPR)，又稱為“假陽率”；縱軸為“真正例率”(False Positive Rate,FPR)，又稱為“真陽率”，

假陽率，簡單通俗來理解就是預測為正樣本但是預測錯了的可能性，顯然，我們不希望該指標太高。

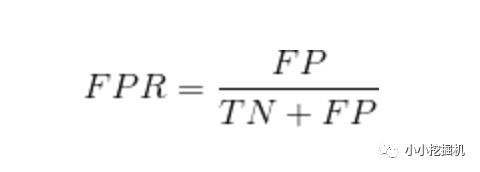
真陽率，則是代表預測為正樣本但是預測對了的可能性，當然，我們希望真陽率越高越好。

ROC計算過程如下：1)首先每個樣本都需要有一個label值，并且還需要一個預測的score值（取值0到1）;2)然后按這個score對樣本由大到小進行排序，假設這些數據位于表格中的一列，從上到下依次降序;3)現在從上到下按照樣本點的取值進行劃分，位于分界點上面的我們把它歸為預測為正樣本，位于分界點下面的歸為負樣本;4)分別計算出此時的TPR和FPR，然后在圖中繪制（FPR, TPR）點。

說這么多，不如直接看圖來的簡單：

AUC（area under the curve）就是ROC曲線下方的面積，如下圖所示，陰影部分面積即為AUC的值：

AUC量化了ROC曲線表達的分類能力。這種分類能力是與概率、閾值緊密相關的，分類能力越好（AUC越大），那么輸出概率越合理，排序的結果越合理。

在CTR預估中，我們不僅希望分類器給出是否點擊的分類信息，更需要分類器給出準確的概率值，作為排序的依據。所以，這里的AUC就直觀地反映了CTR的準確性（也就是CTR的排序能力）。

終于介紹完了，那么這個值該怎么計算呢？

2、AUC的計算

關于AUC的計算方法，如果僅僅根據上面的描述，我們可能只能想到一種方法，那就是積分法，我們先來介紹這種方法，然后再來介紹其他的方法。

2.1 積分思維

這里的積分法其實就是我們之前介紹的繪制ROC曲線的過程，用代碼簡單描述下：

auc = 0.0 height = 0.0 for each training example x_i, y_i： if y_i = 1.0: height = height + 1/(tp+fn) else auc += height * 1/(tn+fp) return auc

在上面的計算過程中，我們計算面積過程中隱含著一個假定，即所有樣本的預測概率值不想等，因此我們的面積可以由一個個小小的矩形拼起來。但如果有兩個或多個的預測值相同，我們調整一下閾值，得到的不是往上或者往右的延展，而是斜著向上形成一個梯形，此時計算梯形的面積就比較麻煩，因此這種方法其實并不是很常用。

2.2 Wilcoxon-Mann-Witney Test

關于AUC還有一個很有趣的性質，它和Wilcoxon-Mann-Witney是等價的，而Wilcoxon-Mann-Witney Test就是測試任意給一個正類樣本和一個負類樣本，正類樣本的score有多大的概率大于負類樣本的score。

根據這個定義我們可以來探討一下二者為什么是等價的？首先我們偷換一下概念，其實意思還是一樣的，任意給定一個負樣本，所有正樣本的score中有多大比例是大于該負類樣本的score？由于每個負類樣本的選中概率相同，那么Wilcoxon-Mann-Witney Test其實就是上面n2（負樣本的個數）個比例的平均值。

那么對每個負樣本來說，有多少的正樣本的score比它的score大呢？是不是就是當結果按照score排序，閾值恰好為該負樣本score時的真正例率TPR？沒錯，相信你的眼睛，是這樣的！理解到這一層，二者等價的關系也就豁然開朗了。ROC曲線下的面積或者說AUC的值 與 測試任意給一個正類樣本和一個負類樣本，正類樣本的score有多大的概率大于負類樣本的score

哈哈，那么我們只要計算出這個概率值就好了呀。我們知道，在有限樣本中我們常用的得到概率的辦法就是通過頻率來估計之。這種估計隨著樣本規模的擴大而逐漸逼近真實值。樣本數越多，計算的AUC越準確類似，也和計算積分的時候，小區間劃分的越細，計算的越準確是同樣的道理。具體來說就是：統計一下所有的 M×N(M為正類樣本的數目，N為負類樣本的數目)個正負樣本對中，有多少個組中的正樣本的score大于負樣本的score。當二元組中正負樣本的 score相等的時候，按照0.5計算。然后除以MN。公式表示如下：

實現這個方法的復雜度為O(n^2 )。n為樣本數(即n=M+N)

2.3 Wilcoxon-Mann-Witney Test的化簡

該方法和上述第二種方法原理一樣，但復雜度降低了。首先對score從大到小排序，然后令最大score對應的sample的rank值為n，第二大score對應sample的rank值為n-1，以此類推從n到1。然后把所有的正類樣本的rank相加，再減去正類樣本的score為最小的那M個值的情況。得到的結果就是有多少對正類樣本的score值大于負類樣本的score值，最后再除以M×N即可。值得注意的是，當存在score相等的時候，對于score相等的樣本，需要賦予相同的rank值(無論這個相等的score是出現在同類樣本還是不同類的樣本之間，都需要這樣處理)。具體操作就是再把所有這些score相等的樣本 的rank取平均。然后再使用上述公式。此公式描述如下：

有了這個公式，我們計算AUC就非常簡單了，下一節我們會給出一個簡單的Demo

3、AUC計算代碼示例

這一節，我們給出一個AUC計算的小Demo，供大家參考：

import numpy as np label_all = np.random.randint(0,2,[10,1]).tolist() pred_all = np.random.random((10,1)).tolist() print(label_all) print(pred_all) posNum = len(list(filter(lambda s: s[0] == 1, label_all))) if (posNum > 0): negNum = len(label_all) - posNum sortedq = sorted(enumerate(pred_all), key=lambda x: x[1]) posRankSum = 0 for j in range(len(pred_all)): if (label_all[j][0] == 1): posRankSum += list(map(lambda x: x[0], sortedq)).index(j) + 1 auc = (posRankSum - posNum * (posNum + 1) / 2) / (posNum * negNum) print("auc:", auc)

輸出為：

[[1], [1], [1], [1], [0], [0], [1], [0], [1], [0]] [[0.3338126725065774], [0.916003907444231], [0.21214487870979226], [0.7598235037160891], [0.07060830328081447], [0.7650759555141832], [0.16157972737309945], [0.6526480840746645], [0.9327233203035652], [0.6581121768195201]] auc: 0.5833333333333334