反向傳播算法(BP算法)是目前用來訓練人工神經網絡的最常用且最有效的算法。作為谷歌機器學習速成課程的配套材料,谷歌推出一個演示網站,直觀地介紹了反向傳播算法的工作原理。
反向傳播算法對于快速訓練大型神經網絡來說至關重要。本文將介紹該算法的工作原理。
簡單的神經網絡
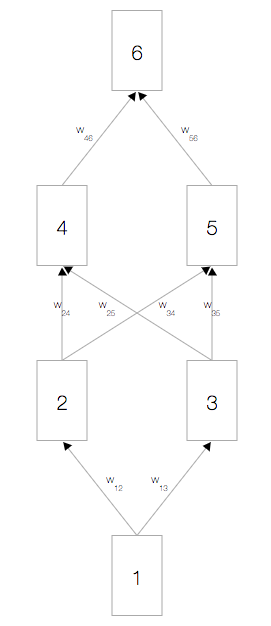
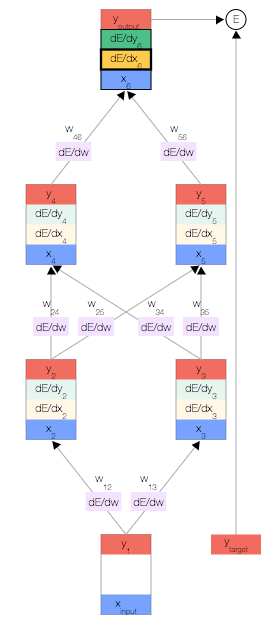
如上圖,你會看到一個神經網絡,其中包含一個輸入節點、一個輸出節點,以及兩個隱藏層(分別有兩個節點)。
激活函數
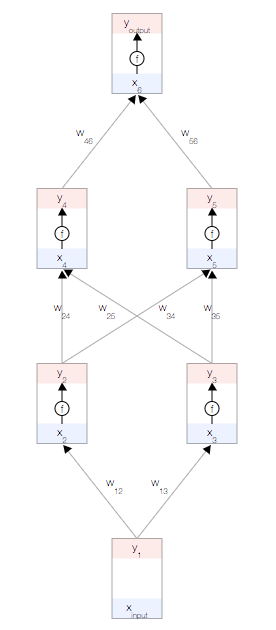
每個節點都有一個總輸入x、一個激活函數f(x)以及一個輸出y=f(x)。
f(x)必須是非線性函數,否則神經網絡就只能學習線性模型。
常用的激活函數是S 型函數:
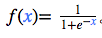
誤差函數
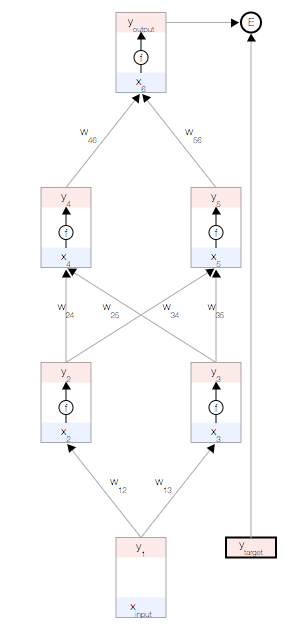
目標是根據數據自動學習網絡的權重,以便讓所有輸入 ?的預測輸出?
?的預測輸出?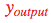 接近目標?
接近目標?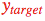
為了衡量與該目標的差距,我們使用了一個誤差函數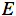 常用的誤差函數是?
常用的誤差函數是?
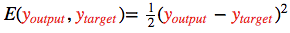
正向傳播
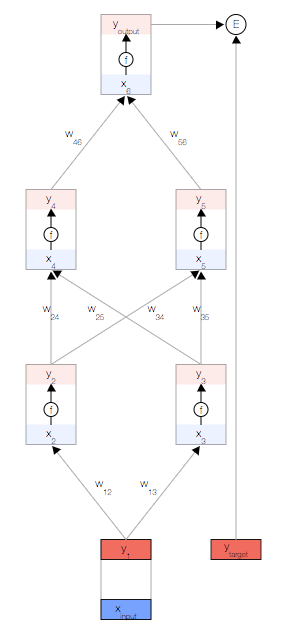
首先,我們取一個輸入樣本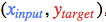 并更新網絡的輸入層。
并更新網絡的輸入層。
為了保持一致性,我們將輸入視為與其他任何節點相同,但不具有激活函數,以便讓其輸出與輸入相等,即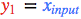
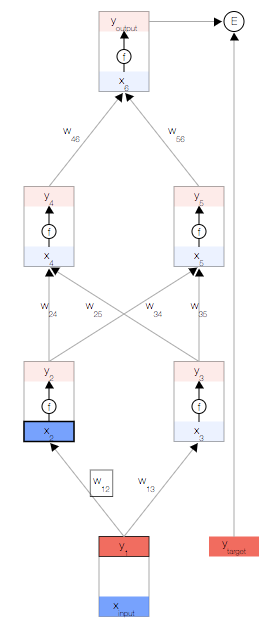
現在,我們更新第一個隱藏層。我們取上一層節點的輸出y,并使用權重來計算下一層節點的輸入x。
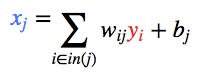
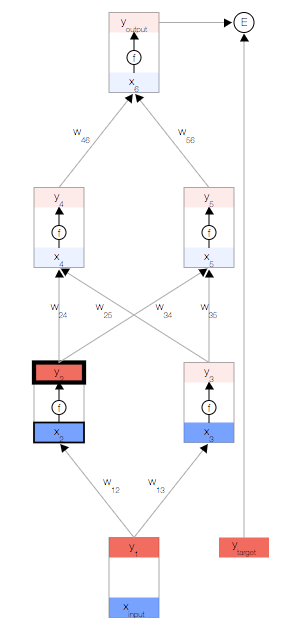
然后,我們更新第一個隱藏層中節點的輸出。 為此,我們使用激活函數f(x)。
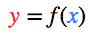
使用這兩個公式,我們可以傳播到網絡的其余內容,并獲得網絡的最終輸出。
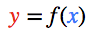
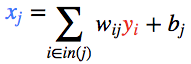
誤差導數
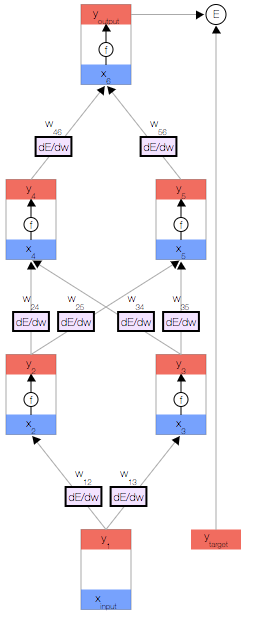
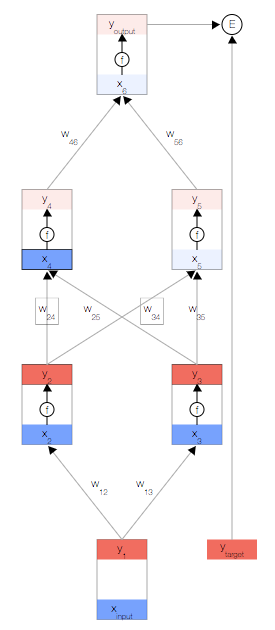
反向傳播算法會對特定樣本的預測輸出和理想輸出進行比較,然后確定網絡的每個權重的更新幅度。 為此,我們需要計算誤差相對于每個權重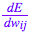 的變化情況。
的變化情況。
獲得誤差導數后,我們可以使用一種簡單的更新法則來更新權重:
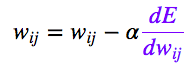
其中,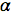 是一個正常量,稱為“學習速率”,我們需要根據經驗對該常量進行微調。
是一個正常量,稱為“學習速率”,我們需要根據經驗對該常量進行微調。
[注意] 該更新法則非常簡單:如果在權重提高后誤差降低了 (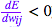 ),則提高權重;否則,如果在權重提高后誤差也提高了 (
),則提高權重;否則,如果在權重提高后誤差也提高了 (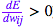 ),則降低權重。
),則降低權重。
其他導數
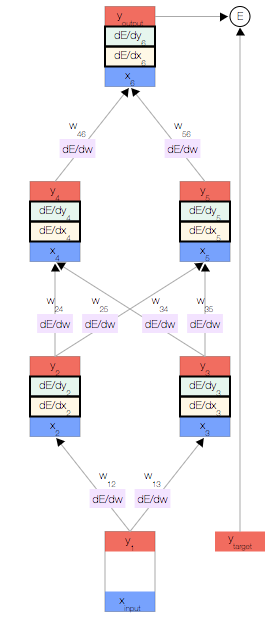
為了幫助計算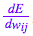 ,我們還為每個節點分別存儲了另外兩個導數,即誤差隨以下兩項的變化情況:
,我們還為每個節點分別存儲了另外兩個導數,即誤差隨以下兩項的變化情況:

反向傳播
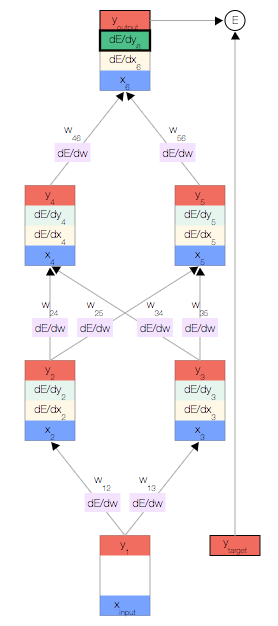
我們開始反向傳播誤差導數。 由于我們擁有此特定輸入樣本的預測輸出,因此我們可以計算誤差隨該輸出的變化情況。 根據我們的誤差函數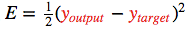 ,我們可以得出:
,我們可以得出:
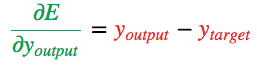
現在我們獲得了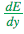 ,接下來便可以根據鏈式法則得出?
,接下來便可以根據鏈式法則得出?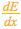 。
。
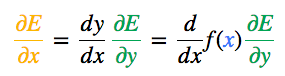
其中,當f(x)是 S 型激活函數時,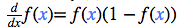
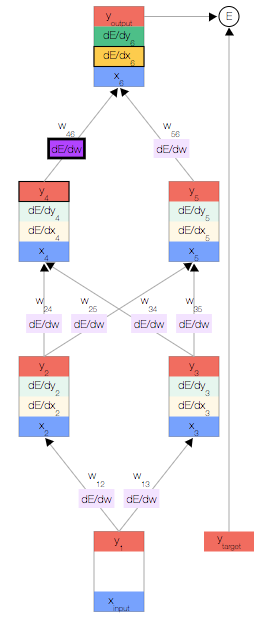
一旦得出相對于某節點的總輸入的誤差導數,我們便可以得出相對于進入該節點的權重的誤差導數。
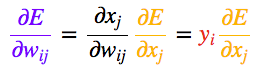
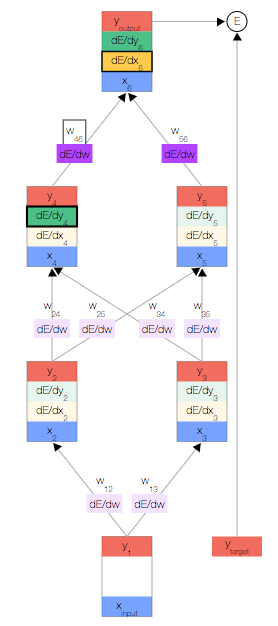
根據鏈式法則,我們還可以根據上一層得出 。此時,我們形成了一個完整的循環。
。此時,我們形成了一個完整的循環。
接下來,只需重復前面的 3 個公式,直到計算出所有誤差導數即可。
結束。
-
神經網絡
+關注
關注
42文章
4779瀏覽量
101165 -
算法
+關注
關注
23文章
4630瀏覽量
93348
原文標題:谷歌官方:反向傳播算法圖解
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
【AI 學習】第六篇--講解BP(反向傳播)流程
MapReduce的誤差反向傳播算法




 反向傳播算法的工作原理
反向傳播算法的工作原理
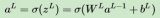











評論