對于一種數(shù)據(jù)結(jié)構(gòu)而言,遍歷是常見操作。二叉樹是一種基本的數(shù)據(jù)結(jié)構(gòu),是一種每個節(jié)點的兒子數(shù)目都不多于2的樹。二叉樹的節(jié)點聲明如下:
typedef struct TreeNode *PtrToNode;
typedef struct TreeNode *BinTree;
struct TreeNode
{
int Data; //為簡單起見,不妨假設樹節(jié)點的元素為int型
BinTree Left;
BinTree Right;
};
二叉樹的遍歷主要有先序遍歷,中序遍歷,后序遍歷,層序遍歷四種方式,下面一一介紹。
1. 先序遍歷
在先序遍歷中,對節(jié)點的訪問工作是在它的左右兒子被訪問之前進行的。換言之,先序遍歷訪問節(jié)點的順序是根節(jié)點-左兒子-右兒子。由于樹可以通過遞歸來定義,所以樹的常見操作用遞歸實現(xiàn)常常是方便清晰的。遞歸實現(xiàn)的代碼如下:
void PreOrderTraversal(BinTree BT)
{
if( BT )
{
printf(“%d\n”, BT->Data); //對節(jié)點做些訪問比如打印
PreOrderTraversal(BT->Left); //訪問左兒子
PreOrderTraversal(BT->Right); //訪問右兒子
}
}
由遞歸代碼可以看出,該遞歸為尾遞歸(尾遞歸即遞歸形式在函數(shù)末尾或者說在函數(shù)即將返回前)。尾遞歸的遞歸調(diào)用需要用棧存儲調(diào)用的信息,當數(shù)據(jù)規(guī)模較大時容易越出棧空間。雖然現(xiàn)在大部分的編譯器能夠自動去除尾遞歸,但是即使如此,我們不妨自己去除。非遞歸先序遍歷算法基本思路:使用堆棧
a. 遇到一個節(jié)點,訪問它,然后把它壓棧,并去遍歷它的左子樹;
b. 當左子樹遍歷結(jié)束后,從棧頂彈出該節(jié)點并將其指向右兒子,繼續(xù)a步驟;
c. 當所有節(jié)點訪問完即最后訪問的樹節(jié)點為空且棧空時,停止。
實現(xiàn)代碼如下:
void PreOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = CreatStack(MAX_SIZE); //創(chuàng)建并初始化堆棧S
while(T || !IsEmpty(S))
{
while(T) //一直向左并將沿途節(jié)點訪問(打印)后壓入堆棧
{
printf("%d\n", T->Data);
Push(S, T);
T = T->Left;
}
if (!IsEmpty(S))
{
T = Pop(S); //節(jié)點彈出堆棧
T = T->Right; //轉(zhuǎn)向右子樹
}
}
}
2. 中序遍歷
中序遍歷的遍歷路徑與先序遍歷完全一樣。其實現(xiàn)的思路也與先序遍歷非常相似。其主要的不同點是訪問節(jié)點順序不同:中序遍歷是訪問完所有左兒子后再訪問根節(jié)點,最后訪問右兒子,即為左兒子-根節(jié)點-右兒子。
遞歸實現(xiàn)的代碼如下:
void InOrderTraversal(BinTree BT)
{
if(BT)
{
InOrderTraversal(BT->Left);
printf("%d\n", BT->Data);
InOrderTraversal(BT->Right);
}
}
非遞歸輔助棧實現(xiàn)代碼如下:
void InOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = CreatStack(MaxSize); //創(chuàng)建并初始化堆棧S
while(T || !IsEmpty(S))
{
while(T) //一直向左并將沿途節(jié)點壓入堆棧
{
Push(S,T);
T = T->Left;
}
if(!IsEmpty(S))
{
T = Pop(S); //節(jié)點彈出堆棧
printf("%d\n", T->Data); //(訪問) 打印結(jié)點
T = T->Right; //轉(zhuǎn)向右子樹
}
}
}
非遞歸不用輔助棧實現(xiàn)中序遍歷:
試設計一個非遞歸算法,按中根順序遍歷非線索二叉樹,但不得用任何輔助棧。在執(zhí)行算法期間,允許改變左孩子指針和右孩子指針的值。
算法:右線索化+回溯
若當前樹的根節(jié)點p有左孩子且未被線索化:將其左孩子的最右結(jié)點(可為左孩子本身)指向p,即右線索化,然后p = p->lChild;
若p有左孩子但已被線索化,說明該p是回溯上來的,即左孩子已經(jīng)被訪問了,則釋放線索化的指針;
若p無左孩子,打印p,向上回溯(即p = p->rChild)。
代碼如下:
/*
輸入:ABDH##I##E##CF#J##G##
*/
#include
typedef struct BTNode* Position;
typedef Position BTree;
typedef char ElementType;
struct BTNode {
ElementType data;
Position lChild, rChild;
};
BTree CreateBTree(void);
void Inorder(BTree bt);
int main()
{
BTree bt = CreateBTree();
Inorder(bt);
return 0;
}
void Inorder(BTree bt)
{
Position p = bt;
while (p)
{
Position pLeft = p->lChild;
if (pLeft)
{
while (pLeft->rChild && pLeft->rChild != p) //找到以p為根結(jié)點的樹的最右孩子
pLeft = pLeft->rChild;
if (pLeft->rChild == NULL) //線索化
{
pLeft->rChild = p;
p = p->lChild;
continue;
}
else //線索化后已被訪問
{
pLeft->rChild = NULL; //釋放指向根節(jié)點(祖先)的指針
}
}
printf("%c ", p->data); //打印
p = p->rChild; //向上回溯或者轉(zhuǎn)向右子樹
}
printf("\n");
}
BTree CreateBTree() //按照先序序列建立二叉樹
{
BTree bt = NULL;
char ch;
scanf("%c", &ch);
if (ch != '#') //'#'代表空節(jié)點
{
bt = new BTNode;
bt->data = ch;
bt->lChild = CreateBTree();
bt->rChild = CreateBTree();
}
return bt;
}
運行結(jié)果:
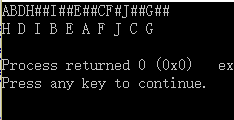
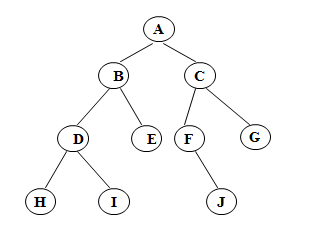
參考博客:http://m.blog.csdn.net/blog/Raito__/40618257
3. 后序遍歷
后序遍歷與中序遍歷,先序遍歷的路徑也完全一樣。主要的不同點是后序遍歷訪問節(jié)點的順序是先訪問左兒子和右兒子,最后訪問節(jié)點,即左兒子-右兒子-根節(jié)點。
遞歸實現(xiàn)思路與中序遍歷和先序遍歷相似,代碼如下:
void PostOrderTraversal(BinTree BT)
{
if (BT)
{
PostOrderTraversal(BT->Left);
PostOrderTraversal(BT->Right);
printf("%d\n", BT->Data);
}
}
后序遍歷的非遞歸實現(xiàn)
思路一:
對于一個節(jié)點而言,要實現(xiàn)訪問順序為左兒子-右兒子-根節(jié)點,可以利用后進先出的棧,在節(jié)點不為空的前提下,依次將根節(jié)點,右兒子,左兒子壓棧。故我們需要按照根節(jié)點-右兒子-左兒子的順序遍歷樹,而我們已經(jīng)知道先序遍歷的順序是根節(jié)點-左兒子-右兒子,故只需將先序遍歷的左右調(diào)換并把訪問方式打印改為壓入另一個棧即可。最后一起打印棧中的元素。代碼如下:
void PostOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S1 = CreatStack(MAX_SIZE); //創(chuàng)建并初始化堆棧S1
Stack S2 = CreatStack(MAX_SIZE); //創(chuàng)建并初始化堆棧S2
while(T || !IsEmpty(S1))
{
while(T) //一直向右并將沿途節(jié)點訪問(壓入S2)后壓入堆棧S1
{
Push(S2, T);
Push(S1, T);
T = T->Right;
}
if (!IsEmpty(S1))
{
T = Pop(S1); //節(jié)點彈出堆棧
T = T->Left; //轉(zhuǎn)向左子樹
}
}
while(!IsEmpty(S2)) //訪問(打印)S2中元素
{
T = Pop(S2);
printf("%d\n", T->Data);
}
}
思路一的優(yōu)點是由于利用了先序遍歷的思想,代碼較簡潔,思路較清晰。缺點是需要用一個棧來存儲樹的所有節(jié)點,空間占用較大。
思路二:
要訪問一個節(jié)點的條件上一個訪問的節(jié)點是右兒子。我們可以增加一個變量Prev來判斷當前節(jié)點Curr的上一個節(jié)點與它的關(guān)系來執(zhí)行相應的操作。
若Prev為空(Curr節(jié)點是根節(jié)點)或者Prev是Curr的父節(jié)點,將Curr節(jié)點的左孩子和右孩子分別壓入棧;
若Prev是Curr的左兒子,則將Curr的右兒子壓入棧;
否則Prev是Curr的右兒子,訪問Curr;
代碼如下:
void PostOrderTraversal(BinTree BT)
{
if(BT == NULL)
return ;
Stack S = CreatStack(MAX_SIZE);
BinTree Prev = NULL , Curr = NULL; //初始化
s.push(BT);
while(!IsEmpty(S))
{
Curr = Top(S); //將棧頂元素賦給Curr
if(Prev == NULL || Prev->Left == Curr || Prev->Right == Curr) //若Prev為NULL或是Curr的父節(jié)點
{
if(Curr->Left != NULL)
Push(S, Curr->Left);
else if(Curr->Right != NULL)
Push(S, Curr->Right);
}
else if(Curr->Left == Prev) //若Prev是Curr的左兒子
{
if(Curr->Right != NULL)
Push(S, Curr->Right);
}
else
{
printf("%d\n", Curr->Data); //訪問當前節(jié)點
Pop(S); //訪問后彈出
}
Prev = Curr; //處理完當前節(jié)點后將Curr節(jié)點變?yōu)镻rev節(jié)點
}
}
4. 層序遍歷
二叉樹遍歷的核心問題是二維結(jié)構(gòu)的線性化。我們通過節(jié)點訪問其左右兒子時,存在的問題是訪問左兒子后,右兒子怎么訪問。因此我們需要一個存儲結(jié)構(gòu)保存暫時不訪問的節(jié)點。前面三種遍歷方式的非遞歸實現(xiàn),我們是通過堆棧來保存。事實上也可以通過隊列來保存。
隊列實現(xiàn)的基本思路:遍歷從根節(jié)點開始,首先將根節(jié)點入隊,然后執(zhí)行循環(huán):節(jié)點出隊,訪問(訪問)根節(jié)點,將左兒子入隊,將右兒子入隊,直到隊列為空停止。
這種遍歷方式的結(jié)果是將二叉樹從上到下,從左至右一層一層的遍歷,即層序遍歷,代碼實現(xiàn)如下:
void LevelOrderTraversal(BinTree BT)
{
BinTree T;
Queue Q; //聲明一個隊列
if (BT == NULL)
return; //如果樹為空,直接返回
Q = CreatQueue(MAX_SIZE); //創(chuàng)建并初始化隊列
AddQ(Q, BT); //將根節(jié)點入隊
while (!IsEmpty(Q))
{
T = DeleteQ(Q); //節(jié)點出隊
printf("%d\n", T->Data); //訪問出隊的節(jié)點
if (T->Left) AddQ(Q, T->Left); //若左兒子不為空,將其入隊
if (T->Right) AddQ(Q, T->Right) //若右兒子不為空,將其入隊
}
}
-
節(jié)點
+關(guān)注
關(guān)注
0文章
220瀏覽量
24526 -
二叉樹
+關(guān)注
關(guān)注
0文章
74瀏覽量
12375
原文標題:二叉樹的遍歷:先序中序后序遍歷的遞歸與非遞歸實現(xiàn)及層序遍歷
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
基于二叉樹的時序電路測試序列設計
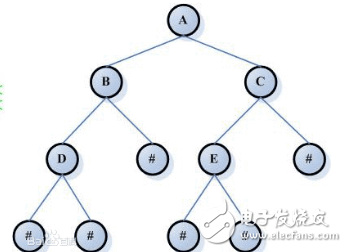
二叉樹層次遍歷算法的驗證
面試算法之重建二叉樹
面試二叉樹看這11個就夠了
二叉樹的前序遍歷非遞歸實現(xiàn)
C語言數(shù)據(jù)結(jié)構(gòu):什么是二叉樹?
怎么就能構(gòu)造成二叉樹呢?
二叉樹的最大深度
解析LeetCode第226號題目:反轉(zhuǎn)二叉樹
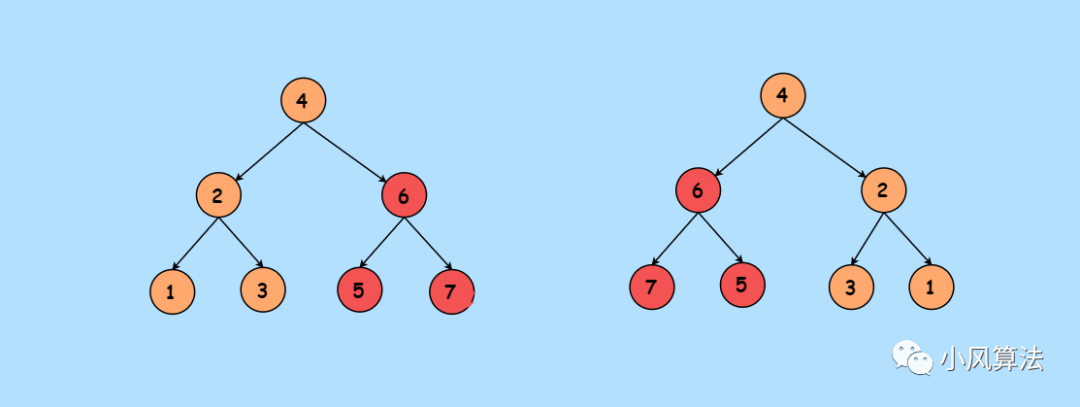




 4中二叉樹的遍歷方式介紹
4中二叉樹的遍歷方式介紹










評論