1 鎖相環基本原理

鎖相環實質為一個閉環的相位調節系統, 基本組成如圖1所示。采用壓控振蕩器輸出與系統輸入之間的誤差信號控制壓控振蕩器輸出頻率。當這兩個信號之間的頻率誤差為零、相位誤差不隨時間變化且誤差控制電壓為定值時, 即認為系統進入鎖定狀態。

圖1中: ur ( t ), θr ( t )為系統輸入電壓參考信號及其相位; e ( t )為誤差信號; uy ( t )為控制信號; uo ( t ), θo ( t )為壓控振蕩器輸出電壓信號及其相位。

2 雙同步坐標系解耦鎖相環基本原理與設計

2.1 雙同步坐標系解耦鎖相環基本原理

假定一個電壓矢量包括正序分量和負序分量, 分別以 ω ^ n ^和 ω ^ m ^的角速度進行旋轉, n表示正序, m表示負序, ω表示基波電網頻率。該電壓矢量可表示為

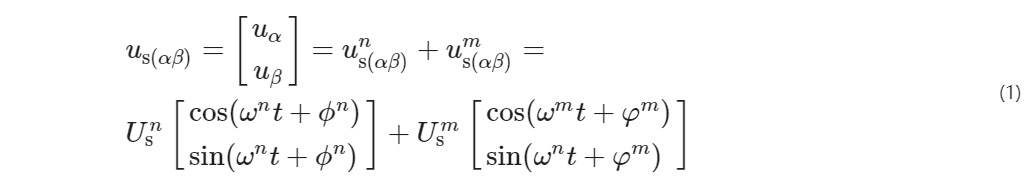
式中: us( αβ ) ^ n ^ , us( αβ ) ^ m ^ ——正序電壓us ^ n ^和負序電壓us ^ m ^在坐標系αβ上的分量;

φ ^ n ^ , φ ^ m ^ ——正序矢量和負序矢量的初始相位。

假設旋轉坐標系分別用 d ^ n ^ q ^ n ^和 d ^ m ^ q ^ m ^表示, θ ^ n ^和 θ ^ m ^為兩個旋轉坐標系的角度, θ ′表示鎖相環輸出角度。若鎖相精確, 即 θ ′= ωt , 則電壓矢量us( αβ ) 在 d ^ n ^ q ^ n ^和 d ^ m ^ q ^ m ^系中可表示為

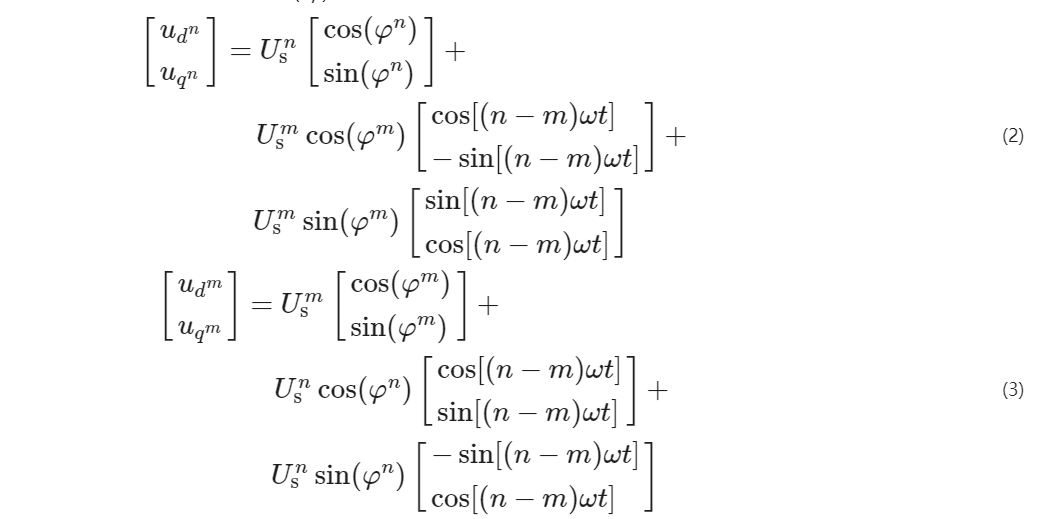
在 d ^ n ^ q ^ n ^與 d ^ m ^ q ^ m ^旋轉坐標系中, 振蕩量的幅值分別由 d ^ m ^ q ^ m ^和 d ^ n ^ q ^ n ^坐標系中的平均值確定。為了對 d ^ n ^ q ^ n ^和 d ^ m ^ q ^ m ^坐標系中的振蕩量進行削弱, 需要對雙同步坐標系解耦鎖相環結構進行設計。

2.2 雙同步坐標系解耦鎖相環結構模型設計

通過以上分析可知, 在正負序dq坐標中各輸出電壓存在一定聯系, 即可進行解耦計算。此處設 n =1, m =－1, 電壓矢量分解到 d ^+1^ q ^+1^和 d ^-1^ q ^-1^兩個同步旋轉坐標系上, 兩個坐標系中的直流分量與電網電壓正負序分量的幅值有很大關系。正序和負序電壓解耦變換公式分別為

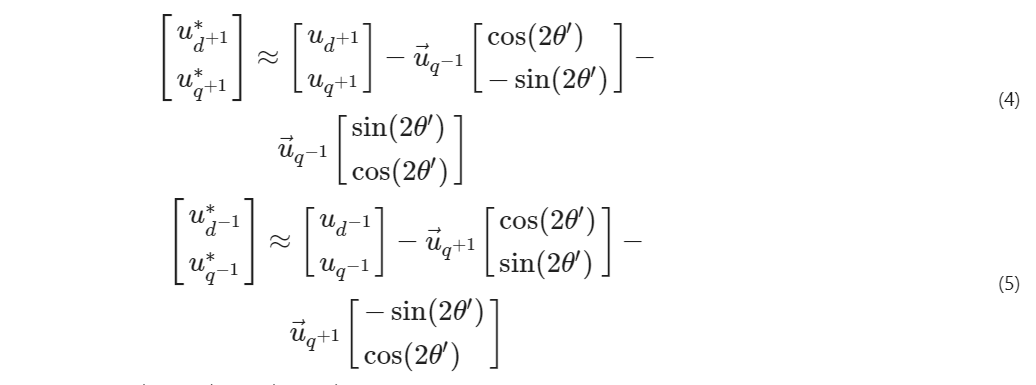
式中: u ~ d ^+1^~ ^ ^ , u ~ q ^+1^~ ^ ^ , u ~ d ^-1^~ ^ ^ , u ~ q ^-1^~ ^ ^ ——解耦后電壓正序和負序dq分量;

u — ~ d ^+1^~ , u — ~ q ^+1^~ , u — ~ d ^－1^~ , u — ~ q ^－1^~ ——濾波后電壓正序和負序dq分量;

θ ′——解耦網絡的電壓輸出相位。

鎖相環控制系統結構如圖 2所示。在不平衡電壓作用下, 正序dq坐標系中q軸電壓 u ~ q ^+1^不僅包括正序分量的直流部分, 還含有負序分量的交流部分, 即uq ^+1^不等于零。通過解耦所得u ~ q ^+1^ ^^ 去除了u*~ q ^+1^~中2次諧波擾動, 從而抑制了不平衡電壓影響。

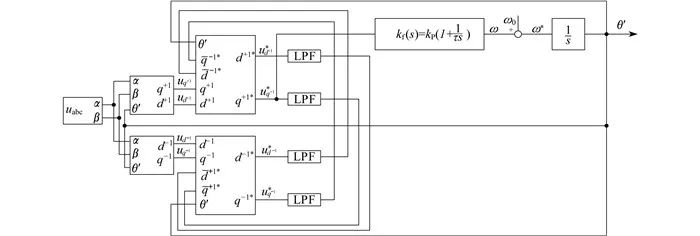
圖 2中LPF(low-pass filter)模塊為低通濾波器(截止頻率為ωf ), 可過濾掉電壓中的高次諧波。其傳遞函數為

2.3 雙同步坐標系解耦鎖相環控制參數設計

圖 2中, 基于雙同步解耦坐標系的鎖相環控制系統含有非線性部分, 故只能對其進行近似性能分析。當相角誤差較小時, 該系統等效傳遞函數可與單同步坐標系鎖相環相同, 系統開環和閉環傳遞函數分別為

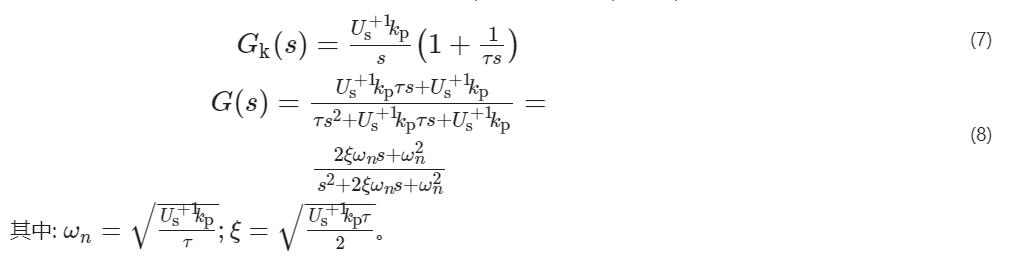
自然振蕩頻率ωn和阻尼系數ξ的大小均與電網電壓分量Us ^+1^有關。由于輸入電壓有時會發生電壓突降等變化, 其控制器參數選擇與單同步坐標系鎖相環相同。

為了分析方便, 假設初始相位角 φ ^+1^ =0, φ ^-1^ =0, 正序分量幅值的階躍響應計算公式為

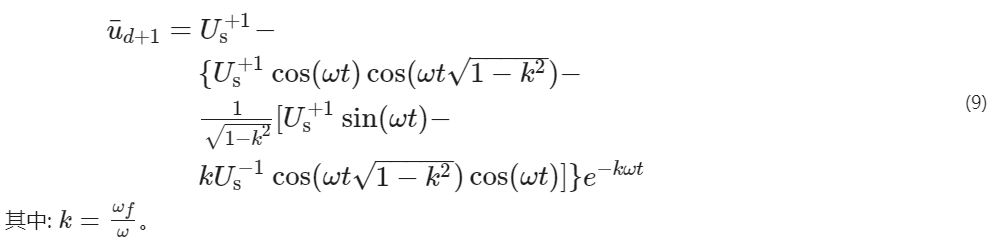
振蕩分量以指數形式衰減, 經過一段時間t后, 正序分量幅值穩定為正序電壓幅值Us ^+1^ 。其穩定時間t與參數k有關。

3 模糊PI雙同步鎖相環設計

3.1 模糊控制器輸入輸出量設計

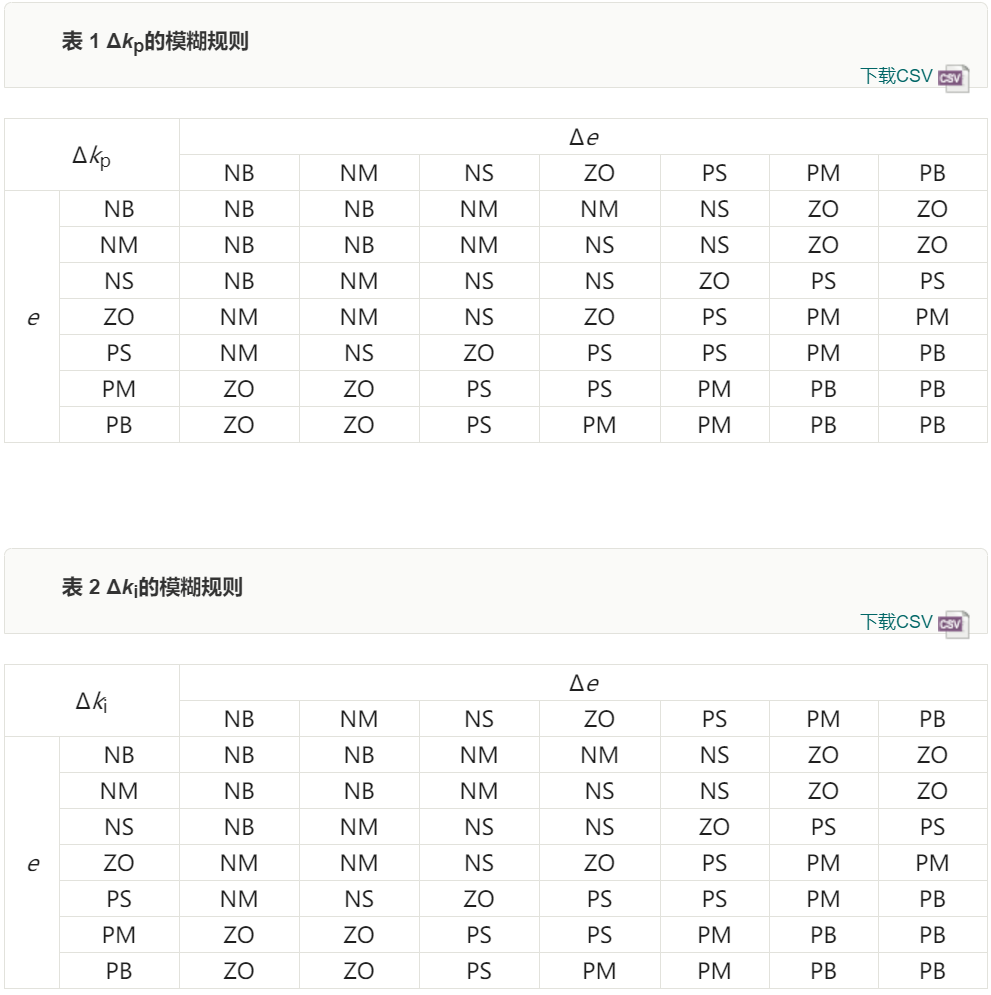
模糊控制器采用雙輸入雙輸出結構, 輸入變量為e及其變化率Δ e , 輸出變量為Δkp與Δki 。根據

雙同步鎖相環仿真結果設置輸入輸出參數, 其中, e ∈[－1, 1], Δ e ∈[－0.1, 0.1], Δkp ∈[－2, 2], Δki ∈[－1, 1]。在輸入輸出語言變量的量化域內取{NB NM NS ZO PS PM PB}7個子集, 輸入輸出量化論域如下:

3.2 隸屬度函數和模糊控制表

模糊邏輯輸入e和Δe以及輸出Δkp和Δki的隸屬度函數取為靈敏性較強的三角函數。面積重心法具有更平滑精準的輸出推理控制, 即使輸入信號發生微小變化, 輸出也會發生變化。為獲得準確的控制量, 反模糊化采用面積重心法, 取隸屬度函數曲線與橫坐標圍成面積的重心為模糊推理的最終輸出值, 即

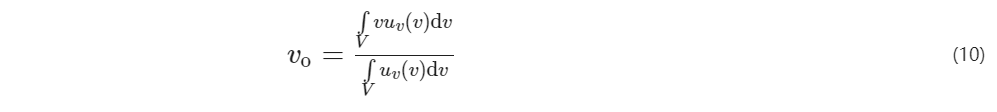
式中: vo ——輸出變量;

V ——輸出論域, v ∈ V ;

uv ——隸屬度。

在MATLAB軟件中完成反模糊化計算。kp與>Δki的模糊規則表如表 1和表 2所示。

4 仿真分析

4.1 仿真模型

為了對基于模糊PI控制的雙同步解耦坐標系三相不平衡鎖相環性能進行驗證, 采用軟件MATLAB Simulink組件進行仿真。

結合其工作原理和系統結構框圖搭建的仿真模型如圖 3所示。

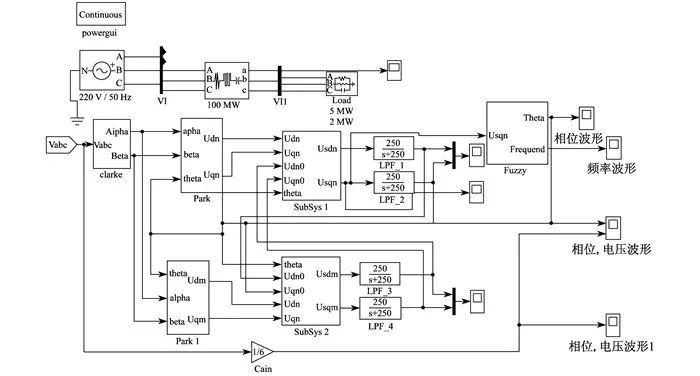
4.2 仿真結果

雙同步解耦坐標系下鎖相環參數設置為: PI控制器

雙同步解耦坐標系下鎖相環參數設置為: PI控制器參數kp >=200, ki =112, 阻尼系數 ξ =0.707, 自然振蕩頻率ωn =35 rad/s, 輸入電壓幅值 U =1.0 p.u.(p.u.為電壓標幺值), 頻率 f =50 Hz。將基于模糊PI控制的雙同步解耦坐標系鎖相環與雙同步和單同步坐標系鎖相環仿真結果進行比較。

4.2.1 電網電壓平衡時仿真結果

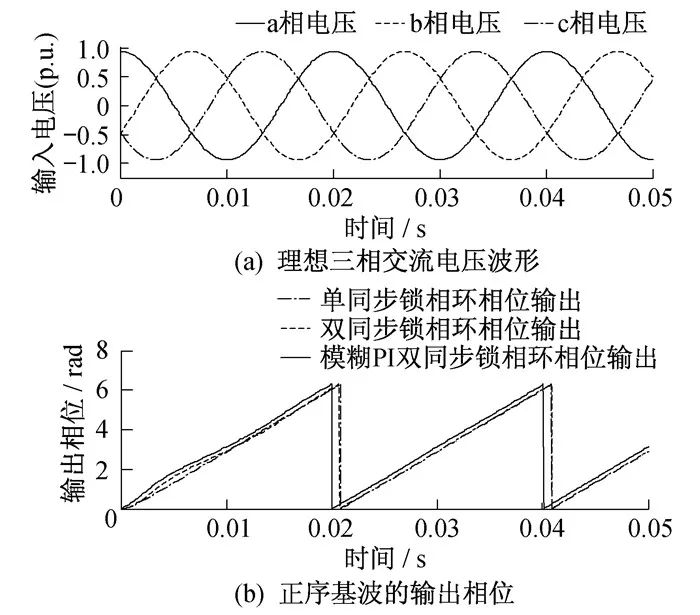
電網電壓平衡時仿真結果如圖 4所示。由圖 4可知, 基于模糊PI控制的雙同步解耦坐標系下三相鎖相可在電網電壓平衡時更快恢復三相電壓且相位輸出波動較小, 能更準確快速地鎖定正序基波相位信息。

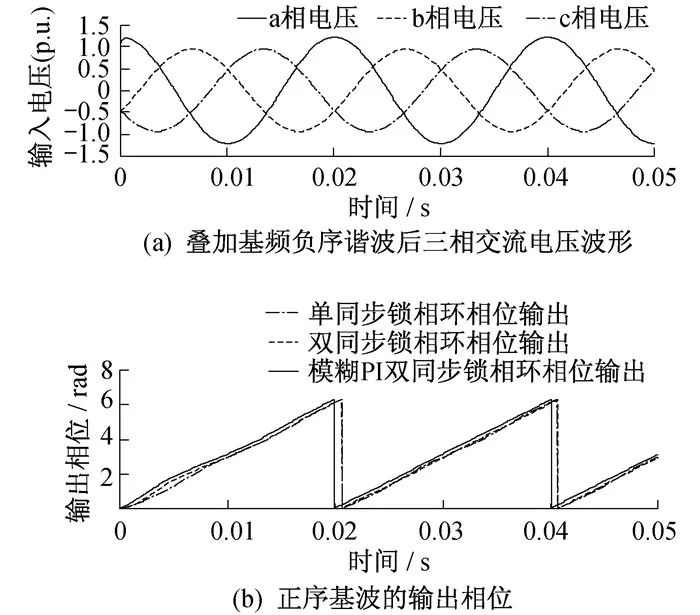
在理想輸入電壓上疊加0.3 p.u.且初始相位為30°的基頻負序諧波, 仿真結果如圖 5所示。模糊PI控制的雙同步解耦坐標系三相鎖相環在電網電壓出現基頻負序諧波時, 因其可在線調整PI參數, 故能更快速恢復三相電壓消除負序諧波對系統的影響, 更準確快速鎖定正序基波的相位信息, 提高系統抗不平衡電壓干擾的能力。

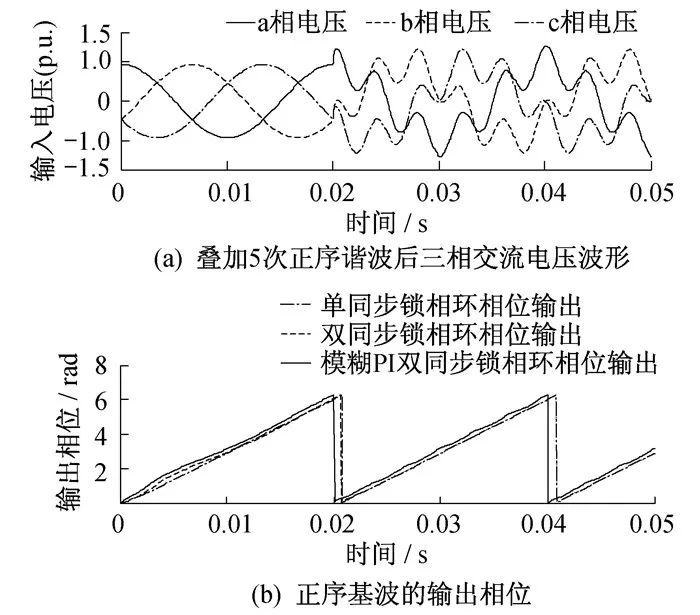
4.2.3 低次諧波輸入時仿真結果

在0.02 s時理想輸入電壓上疊加0.2 p.u.的5次正序諧波。低次諧波輸入時的仿真結果如圖 6所示。當電壓含一定諧波時, 由于鎖相結構中含有濾波器, 能對諧波起到很好的抑制作用。

由圖 5和圖 6可知, 相比單同步和雙同步解耦坐標系下的鎖相環, 基于模糊PI控制的雙同步解耦坐標系鎖相環在電網電壓含有基頻負序諧波、多頻正序諧波時能更準確、快速地鎖定相位信息并檢測到相位誤差畸變小。

4.2.4 相位突變時仿真結果

在0.02 s時理想輸入電壓相位增加20°, 相位突變時的仿真結果如圖 7所示。

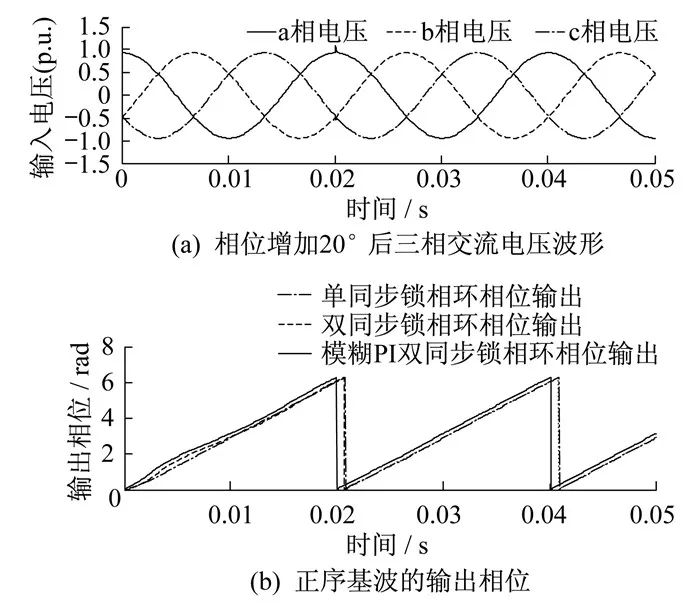
由圖 7可知, 模糊PI控制下的單同步、雙同步鎖相環在電壓相位突變時均能保持正常電壓波形, 但模糊PI控制的雙同步鎖相環能更快消除電壓相位突變給系統造成的沖擊, 鎖定相位速度更快, 具有更好的動態特性。

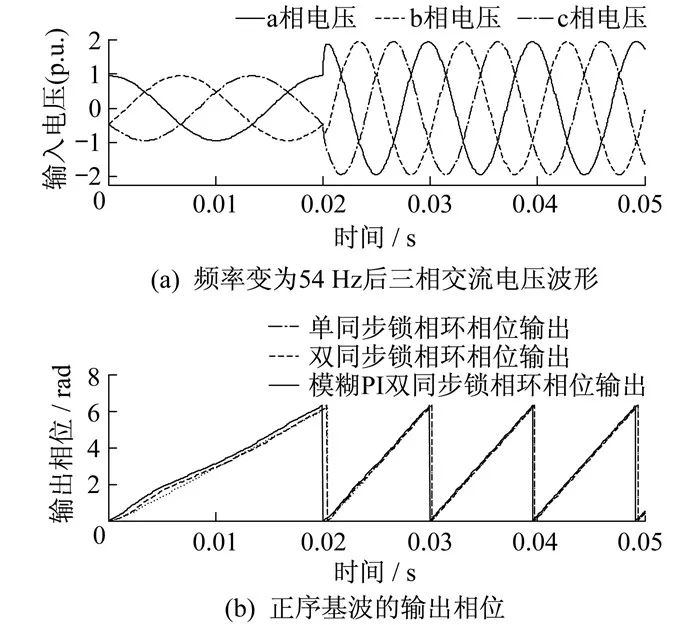
4.2.5 頻率突變時仿真結果

在0.02 s時理想輸入電壓頻率從50 Hz變為54 Hz, 頻率突變時的仿真結果如圖 8所示。由圖 8可知, 單同步和雙同步解耦坐標系下的鎖相環在電網電壓頻率突變時均可鎖定正序基波相位信息并平穩地跟蹤頻率和相位變化, 但模糊PI控制的雙同步解耦坐標系鎖相環鎖定相位速度更快, 對諧波有更強的抑制作用, 表現出良好的頻率適應性。

5 結語

針對雙同步鎖相環系統在電網發生不平衡或畸變時不能對正序基波分量的幅值和相位精確實時檢測的問題, 本文在雙同步鎖相環的基礎上, 提出了基于模糊PI控制的雙同步解耦坐標系三相不平衡鎖相環, 通過解耦網絡實現電網電壓正序基波分量分離, 并對分離出的正序基波分量的幅值和相位等信息進行精確快速檢測。模糊PI控制的雙同步解耦坐標系鎖相環在運行中通過不斷檢測誤差及其變化率, 依據模糊規則對PI參數進行在線修正, 很好地避免了傳統鎖相環以一組固定不變的PI參數在控制過程中運行調節的缺點, 且在電網不平衡時能更快速、精確地對正序基波分量的幅值和相位進行檢測, 保證了分布式系統并網時對鎖相精度的要求。本文仿真結果驗證了所提方法的有效性。