每次想弄清楚零極點的物理本質是什么,如何對系統產生影響(大學信號與系統沒好好學),網上找一下相關內容,總能看到 ”Hs=A0/(s+a) 極點為s=-a s=jw 所以w=a時增益-20db/十倍頻 “類似的結論。
雖然也可以分析電路,但仔細想一想總讓人一臉懵逼。s不是等于σ+jw嗎,怎么變成了jw,jw又變成了w,而且w=-a又變成了w=a。每次都想把信號與系統重新學一遍(只能怪自己大學摸魚去了),但看著厚厚的上下冊,拖了又拖...... 最近剛好空一點,整理了一些相關內容。
傅里葉變換和拉普拉斯變換:
傅里葉變換 :將時域函數轉換為不同頻率的正弦波的疊加。
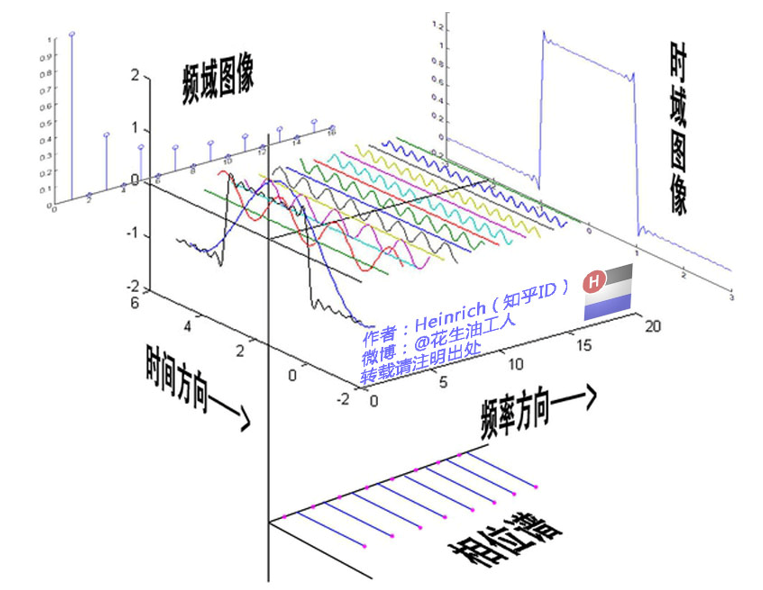
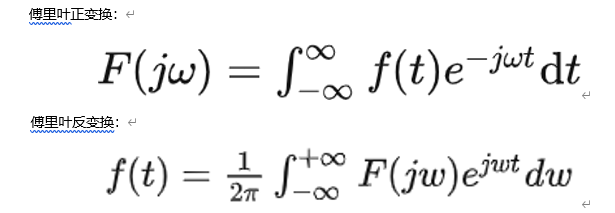
拉普拉斯變換 :
由于傅里葉變換的局限性,要保證f(t)收斂,因此對于非收斂的函數,添加一個衰減因子e ^-σt^ ,使函數在t→∞時,f(t)→0。然后再進行傅里葉變換。


極點的意義:
H(s)=H0/(s-a) 極點s=a 對應的時域原函數:Ht=H0*e^at
由上述分析可知,Hs是Ht×衰減因子做傅里葉變換得到,Gt=H0e^ate^-σt=H0*e^-(σ-a)t 要使Gt收斂,則必須σ>a。
因此可知道極點s=a,是σ+jw=a ,并非jw=a。即σ=a。
極點代表的時域函數可進行拉式變換的收斂域,σ需在極點的右方(見下圖,execl做的簡易示圖,勿噴):
(對于虛數極點s=a+bj,代表σ=a,w=b,a反應衰減速率,b反應震蕩頻率,虛數極點后續有時間再具體分析)
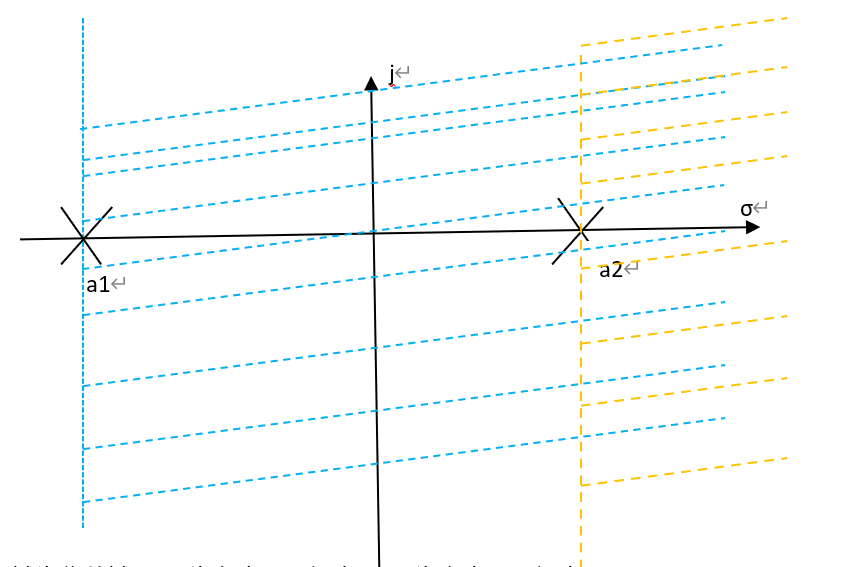
圖中陰影部分為收斂域,a1為左半平面極點,收斂域在a1右側,a2為右邊平面極點,收斂域同樣在右側。
由此可由極點位置判斷系統穩定性:
左半平面極點:收斂域經過原點,說明σ=0時,時域函數f(t)** e^-σt *收斂,即f(t)收斂。
右半平面極點:收斂域大于零,說明f(t)** e^-σt *中σ必須大于0才收斂,即f(t)不收斂。
另一個問題,為什么s=σ+jw 又有s=jw。其實也就是s域函數與電路的頻率響應的轉換。
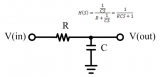
交流時電容容抗Zc=1/jwc
因此s=jw 只是分別在s域和頻域里數學形式上相同,電感同理。
因此知道傳輸函數Hs,令s=jw可得到電路的頻率響應H(w) (此Hw并不是傅里葉變換的Hw)
有了頻響函數,電路的幅頻特性,相頻特性都能很簡單的計算出來。
-
頻率響應
+關注
關注
1文章
102瀏覽量
18355 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42667 -
拉普拉斯變換
+關注
關注
1文章
32瀏覽量
10177 -
零極點
+關注
關注
1文章
10瀏覽量
3050
發布評論請先 登錄
相關推薦




 零極點的物理本質是什么?如何對系統產生影響?
零極點的物理本質是什么?如何對系統產生影響?
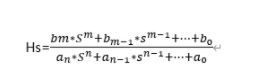










評論