傅里葉級數有時移特性
傅里葉級數是指將周期函數分解為一系列正弦函數和余弦函數的和的表達式。它得名于法國數學家傅里葉,被廣泛應用于信號處理、圖像處理、噪聲分析等領域。傅里葉級數的最重要的特征之一就是時移特性。在本文中,我們將介紹傅里葉級數的時移特性以及它在實際應用中的作用。
一、傅里葉級數基礎
傅里葉級數可用于表示具有周期性的函數。 周期函數可以表示為正弦函數和余弦函數的和的形式,如下所示:
$$ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n{cos~n\omega}x+b_n{sin~n\omega}x) $$
其中,$\omega$ 是頻率,$a_n$ 和 $b_n$ 是函數 $f(x)$ 的傅里葉系數。傅里葉系數可以通過對 $f(x)$ 進行積分來計算,具體如下:
$$ a_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x){cos~n\omega}x\ dx, $$
$$ b_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x){sin~n\omega}x\ dx $$
其中 $T$ 是函數 $f(x)$ 的周期。
二、傅里葉級數的時移特性
傅里葉級數的時移特性是指在時間軸上對函數進行平移,它仍可以表示為一系列正弦函數和余弦函數的和。 如果我們將函數 $f(x)$ 平移 $a$ 個單位(即 $f(x-a)$),則其傅里葉級數可以表示為:
$$ f(x-a) = \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n{cos~n\omega}(x-a)+b_n{sin~n\omega}(x-a)) $$
我們可以將傅里葉系數展開后得到:
$$ a_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x-a){cos~n\omega}x\ dx, $$
$$ b_n=\frac{2}{T}\int_{-T/2}^{T/2}f(x-a){sin~n\omega}x\ dx $$
這說明傅里葉系數中只是函數 $f(x)$ 中的自變量 $x$ 發生了變化,而其他部分保持不變。 因此,平移不會改變傅里葉系數的值,而只是改變了自變量的值。 因此,傅里葉級數具有時移的特性。
三、時移的應用
傅里葉級數的時移特性在信號處理和圖像處理等領域中得到了廣泛的應用。在這些領域中,我們通常需要將信號或圖像進行平移,以便進行分析或處理。 在這種情況下,我們可以使用傅里葉級數,而無需重新計算傅里葉系數。
例如,圖像處理中的圖像對齊需要將兩幅圖像平移,使它們對齊。 如果我們需要對齊的兩幅圖像的頻譜是已知的,那么我們只需移動頻譜圖像,而無需重新計算它們的傅里葉系數。
除此之外,時移特性還被廣泛運用于測量信號的延遲。通過對信號進行逆傅里葉變換,可以獲得函數在時間域中的表示,并通過平移進行信號的延遲測量。
四、總結
傅里葉級數具有時移特性,因此我們可以在函數 $f(x)$ 平移時,使用原有的傅里葉系數,而無需重新計算。這種特性在信號和圖像處理中有重要的應用,可以簡化許多分析和處理任務。通過使用傅里葉級數的時移特性,我們可以更加高效地工作并取得更好的結果。
-
圖像處理器
+關注
關注
1文章
104瀏覽量
15562 -
信號處理器
+關注
關注
1文章
254瀏覽量
25350 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42709
發布評論請先 登錄
相關推薦
VirtualLab Fusion案例:傅科刀口測試的建模
VirtualLab Fusion案例:單分子顯微鏡高NA成像系統的建模
VirtualLab Fusion案例:高NA傅里葉單分子成像顯微鏡
低壓配電中產生的諧波應該如何治理?
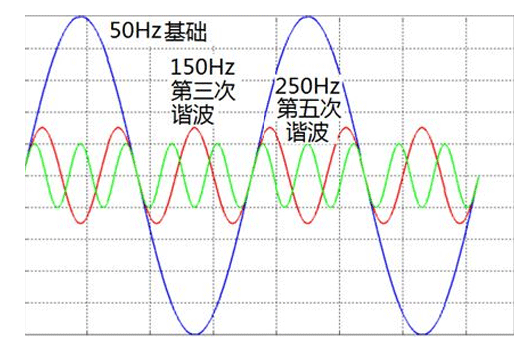
傅里葉變換在信號處理中的應用
傅里葉變換的數學原理
大華股份與中移鐵通簽署戰略合作協議
傅里葉半導體榮獲季豐電子AEC-Q100與AEC-Q006證書
工業級數字鉗形表的選型要點和用途

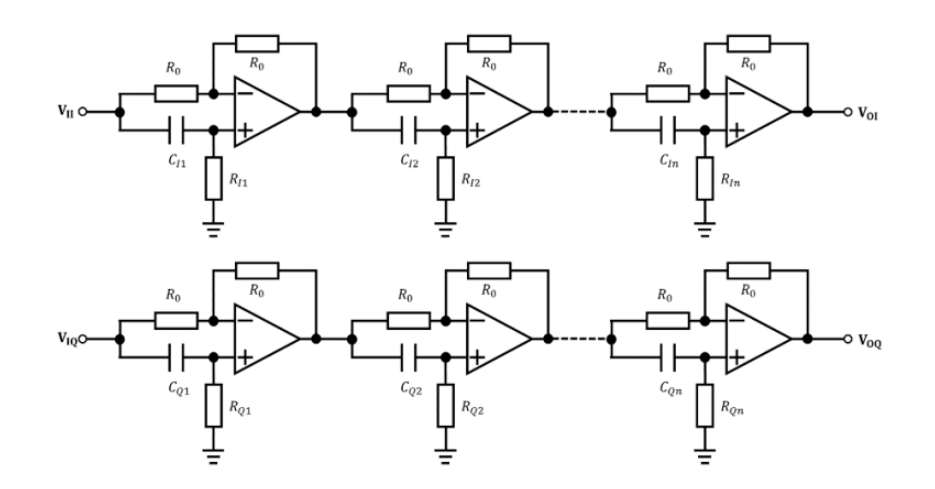
什么是移相網絡?移相網絡的電路結構




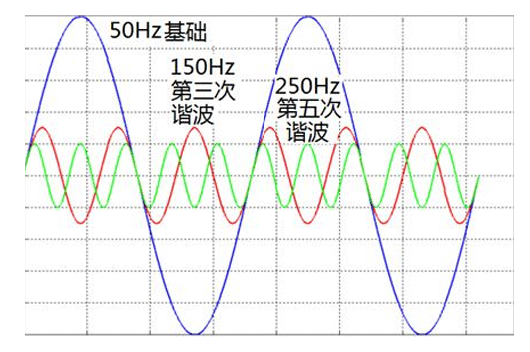
 傅里葉級數有時移特性
傅里葉級數有時移特性










評論