**Poly基本原理介紹 **

考慮到許多讀者可能對Poly并不了解，而且許多Poly文獻讀起來也比較抽象，我們先簡單介紹一下Poly的工作原理。我們力圖用最簡單的代數與幾何描述來解釋Poly的基本原理。這部分內容參考了文獻[12]的圖片，我們通過解讀這些圖片來解釋其中原理。

首先，我們假設有如圖1所示的一段簡單的循環嵌套，其中N為常數。循環嵌套內語句通過對A[i-1][j]和A[i][j-1]存儲數據的引用來更新A[i][j]位置上的數據。如果我們把語句在循環內的每一次迭代實例抽象成空間上的一個點，那么我們可以構造一個以(i,j)為基的二維空間，如圖2所示。圖中每個黑色的點表示寫入A[i][j]的一次語句的迭代實例，從而我們可以構造出一個所有黑色的點構成的一個矩形，這個矩形就可以看作是二維空間上的一個Polyhedron（多面體），這個空間稱為該計算的迭代空間。

圖1 一段簡單的代碼示例

圖2 圖1示例代碼的迭代空間

我們可以用代數中的集合來對這個二維空間上的Polyhedron進行表示，即{[i, j] : 1 <= i <= N - 1 and 1 <= j <= N – 1}，其中[i, j]是一個二元組，“:”后面的不等式表示這個集合的區間。我們可以給這個二元組做一個命名，叫做S，表示一個語句，那么這個語句的Polyhedron就可以表示成{S[i, j] : 1 <= i <= N - 1 and 1 <= j <= N – 1}。

由于語句S是先迭代i循環再迭代j循環，因此我們可以給語句S定義一個調度（順序），這個調度用映射表示，即{ S[i, j] -> [i, j] }，表示語句S[i, j] 先按i的順序迭代再按照j的順序迭代。

接下來，我們來分析語句和它訪存的數組之間的關系，在代數中我們用映射來表示關系。圖1中語句S對數組A進行讀和寫，那么我們可以用Poly來計算出S和A之間的讀訪存關系，可以表示成{ S[i, j] -> A[i - 1, j] : 1 <= i <= N -1 and 1 <= j <= N- 1; S[i, j] -> A[i, j - 1] : 1 <= i <= N - 1 and 1 <= j <= N -1 } 。同樣地，寫訪存關系可以表示成{ S[i, j] -> A[i, j] : 1 <= i <= N - 1 and 1 <= j <= N -1 }。

基于這個讀寫訪存關系，Poly就可以計算出這個循環嵌套內的依賴關系，這個依賴關系可以表示成另外一種映射關系，即{ S[i, j] -> S[i, 1 + j] : 1 <= i <= N - 1 and 1 <= j <=N - 2; S[i, j] -> S[i + 1, j] : 1 <= i <= N - 2 and 1 <= j <= N- 1 }。

可以注意到，Poly對程序的表示都是用集合和映射來完成的。當我們把語句實例之間的依賴關系用藍色箭頭表示在迭代空間內時，就可以得到如圖3所示的形式。根據依賴的基本定理[13]，沒有依賴關系的語句實例之間是可以并行執行的，而圖中綠色帶內（對角線上）的所有點之間沒有依賴關系，所以這些點之間可以并行執行。但是我們發現這個二維空間的基是(i, j)，即對應i和j兩層循環，無法標記可以并行的循環，因為這個綠色帶與任何一根軸都不平行。所以Poly利用仿射變換把基(i, j)進行變換，使綠色帶能與空間基的某根軸能夠平行，這樣軸對應的循環就能并行，所以我們可以將圖3所示的空間轉化成如圖4所示的形式。

此時，語句S的調度就可以表示成{ S[i, j] -> [i + j, j]}的形式。所以Poly的變換過程也稱為調度變換過程，而調度變換的過程就是變基過程、實現循環變換的過程。

圖3 帶依賴關系的迭代空間

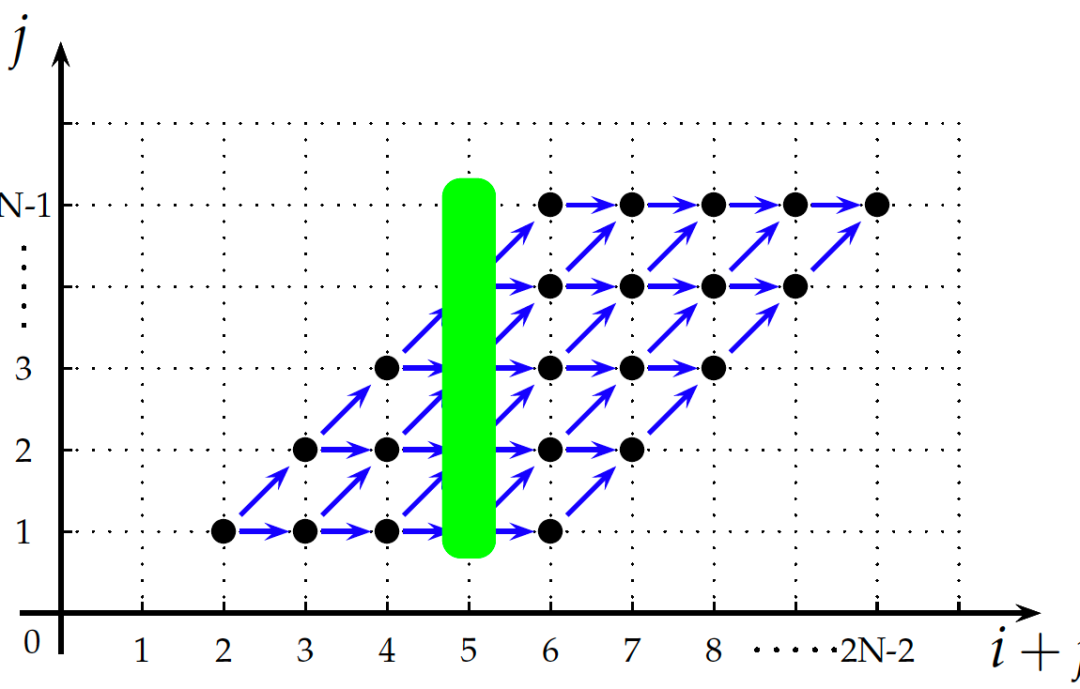
圖4 變基之后的迭代空間

圖4中綠色帶和j軸平行，這樣在代碼中表示起來就方便了。我們說Poly做循環變換的過程就是將基(i, j)變成(i + j, j)的一個過程，也就是說，Poly的底層原理就是求解一個系數矩陣，這個系數矩陣能夠將向量(i, j)轉換成向量(i + j, j)。

根據這樣的調度，Poly就可以利用它的代碼生成器，生成如圖5所示的代碼。此時，內層循環就可以并行了。（注：這里示意的是“源到源”翻譯的Poly編譯器，也就是Poly生成的代碼還需要交給基礎編譯器如GCC、ICC、LLVM等編譯成機器碼才能運行。也有內嵌在基礎編譯中的Poly工具。）

圖5 Poly變換后生成的代碼

當然，我們這里舉的例子是一個很簡單的例子，在實際應用中還有很多復雜的情況要考慮。Poly幾乎考慮了所有的循環變換，包括Interchange（交換）、Skewing/Shifting（傾斜/偏移）、Reversal（反轉）、Tiling/Blocking（分塊）、Stripe-mining、Fusion（合并）、Fission/Distribution（分布）、Peeling（剝離）、Unrolling（展開）、Unswitching、Index-set splitting、Coalescing/Linearization等，圖6～8[14]中給出了幾種Poly中實現的循環變換示意圖，右上角的代碼表示原輸入循環嵌套，右下角的代碼表示經過Poly變換后生成的代碼。圖中左邊的集合和映射關系的含義分別為：J代表原程序語句的迭代空間，S表示輸入程序時的調度，T表示目標調度，ST就是Poly要計算的調度變換。

圖6 Poly中skewing變換示意圖

圖7 Poly中Fusion變換示意圖

圖8 Poly中Tiling變換示意圖

深度學習應用的Poly優化

讓我們以圖9中所示的二維卷積運算（矩陣乘法）為例來簡單介紹Poly是如何優化深度學習應用的。

圖9 一個2D卷積示例

Poly會將循環嵌套內的計算抽象成一個語句。例如圖9中S1語句表示卷積初始化，S2代表卷積歸約；而S0和S3則分別可以看作卷積操作前后的一些操作，比如S0可以想象成是量化語句，而S3可以看作是卷積后的relu操作等。

為了便于理解，我們以CPU上的OpenMP程序為目標對圖9中的示例進行變換。Poly在對這樣的二維卷積運算進行變換的時候，會充分考慮程序的并行性和局部性。如果我們對變換后的程序并行性的要求大于局部性的要求，那么Poly會自動生成如圖10所示的OpenMP代碼；如果我們對局部性的要求高于并行性，那么Poly會自動生成如圖11所示的OpenMP代碼。（注：不同的Poly編譯器生成的代碼可能會因采用的調度算法、編譯選項、代碼生成方式等因素而不同。）

圖10 Poly生成的OpenMP代碼——并行性大于局部性

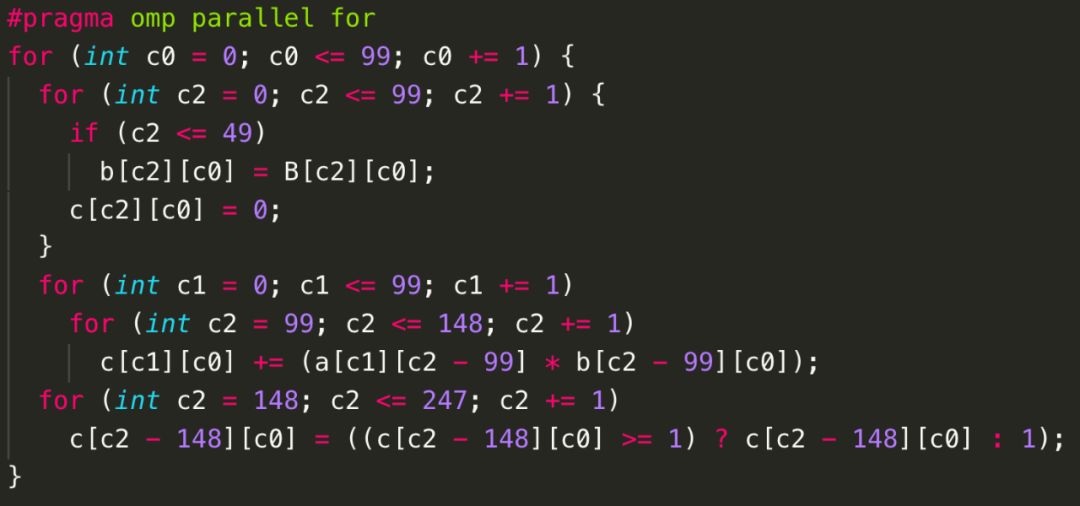
圖11 Poly生成的OpenMP代碼——局部性大于并行性

通過對比圖10和圖11，兩種生成的代碼采用的循環fusion（合并）策略不同：圖10中所示的代碼采用了({S0}, {S1, S2, S3})的合并策略，圖11中生成的代碼則使用了({S0,S1, S2, S3})的合并策略，但是必須通過對S2向右偏移99次、S3向右偏移148次，以及循環層次的interchange（交換）來實現這樣的合并。顯然，圖11所示的代碼局部性更好。而并行性上，仔細研究后不難發現，圖11生成的代碼中，只有最外層c0循環是可以并行的，而圖10代碼中，S0語句的c0、c1循環都可以并行，并且包含S1、S2、 S3三條語句的循環嵌套的c0、c1循環也都可以并行，相對于圖11代碼，圖10生成的代碼可并行循環的維度更多。

當然，在面向CPU生成OpenMP代碼時，多維并行的優勢沒有那么明顯，但是當目標架構包含多層并行硬件抽象時，圖9中的代碼能夠更好地利用底層加速芯片。例如，當面向GPU生成CUDA代碼時，而圖10對應的CUDA代碼（如圖12所示）由于合并成了兩個部分，會生成2個kernel，但是每個kernel內c0維度的循環被映射到GPU的線程塊上，而c1維度的循環被映射到GPU的線程上；圖11對應的CUDA代碼（如圖13所示）只有1個kernel，但是只有c0維度的循環被映射到GPU的線程塊和線程兩級并行抽象上。為了便于閱讀，我們并未開啟GPU上shared memory和private memory自動生成功能。從圖中也不難發現，Poly也可以自動生成線程之間的同步語句。（注：圖中循環分塊大小為32，圖12中線程塊上線程布局為3216，圖13中為324*4。）

圖12 Poly生成的CUDA代碼——并行性大于局部性

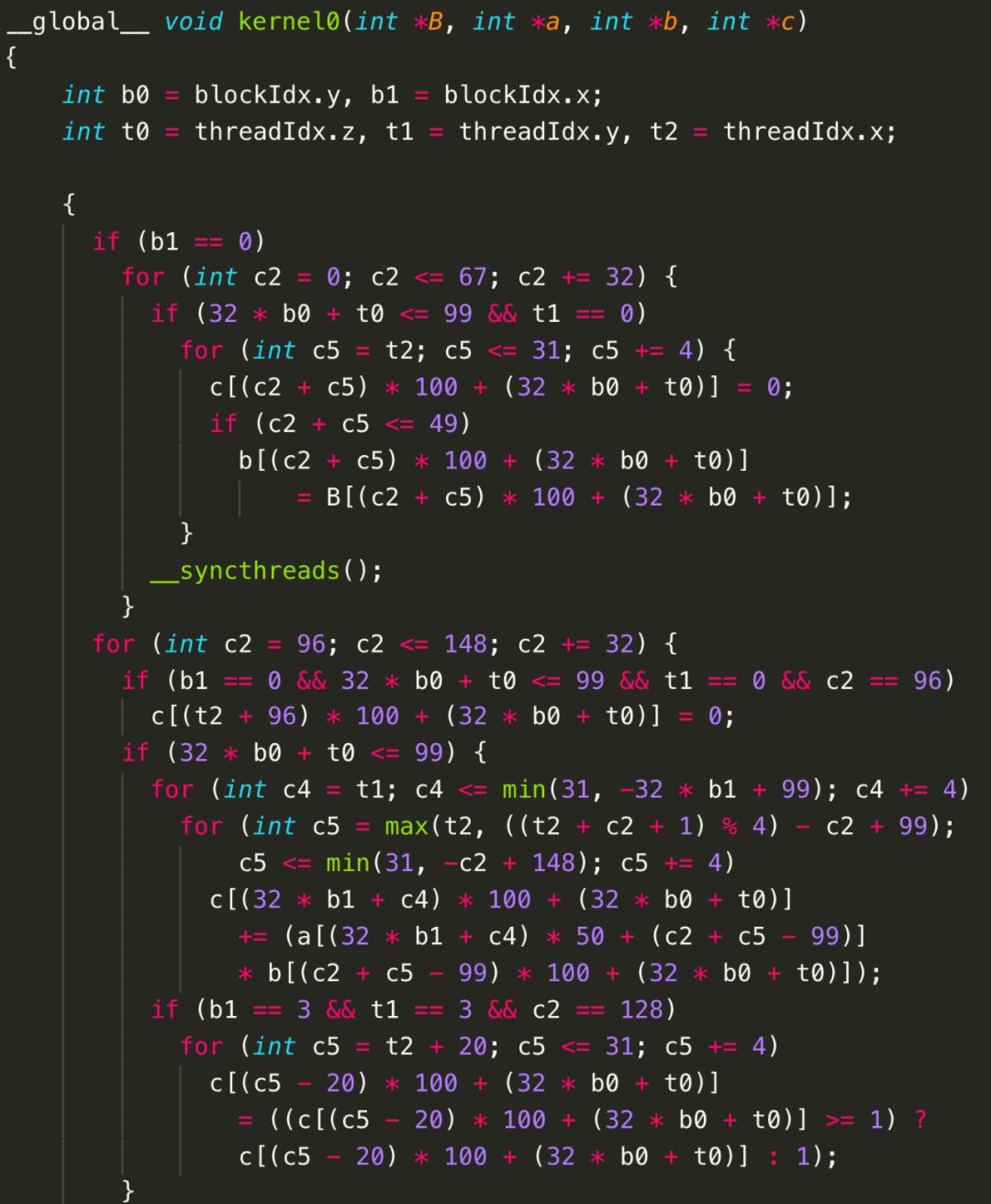
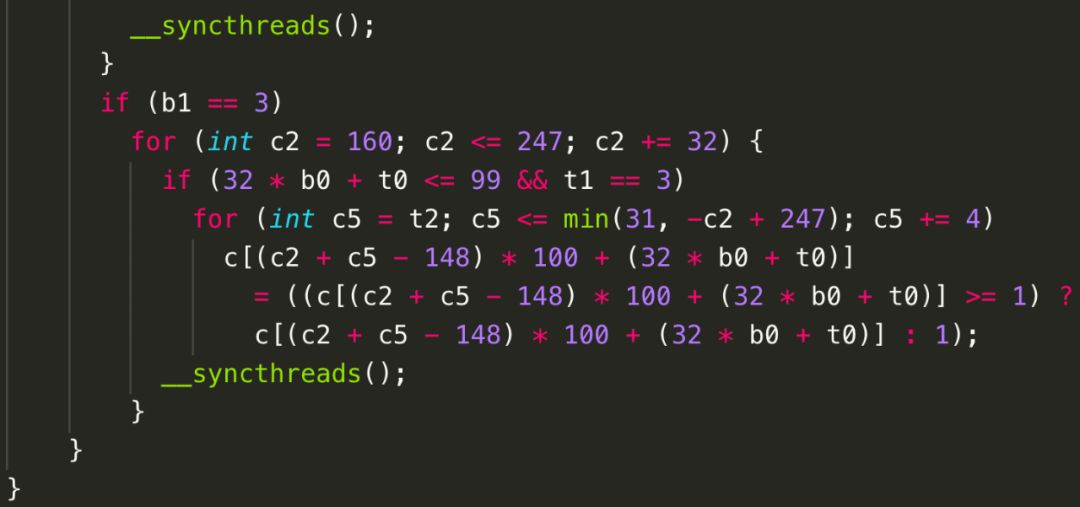
圖13 Poly生成的CUDA代碼——局部性大于并行性

值得注意的是，為了充分挖掘程序的并行性和局部性，Poly會自動計算出一些循環變換來實現有利于并行性和局部性的變換。例如，為了能夠達到圖11和圖13中所有語句的合并，Poly會自動對S2和S3進行shifting（偏移）和interchange（交換）。