傳輸線的損耗有介質損耗,導體損耗和輻射損耗。
下面,從麥克斯韋方程,來看看傳輸線的介質損耗。
具體流程是這樣的:
(1) 麥克斯韋方程推導出波動方程
(2) 給出假設條件,然后得到波動方程的解,即波的表達形式
(3) 有耗媒質可以用損耗角正切來表征
(4) 看波在有耗媒質中傳播時的表達形式
麥克斯韋有四個方程,其相量形式為:

假設傳輸線處于介電材料中。
所謂介電材料,就是當在其上施加一個電場后,會使得材料的分子或者原子發生極化,產生電偶極矩,從而改變整體的位移通量。
即:
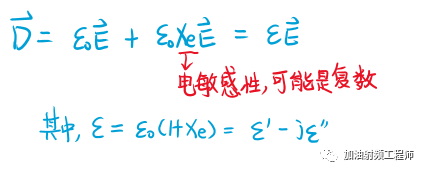
假設所分析的傳輸線所處的區域是無源的,則可以做出如下的推導,得出波動方程。
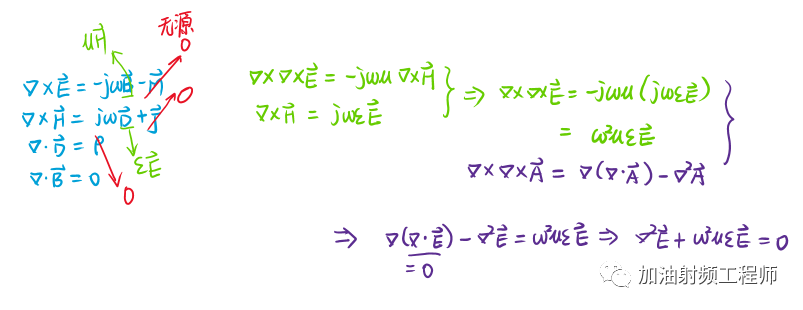
然后假設電場只有x分量,且Ex不隨x和y變化,即:
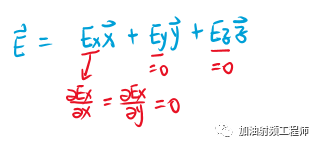
所以波動方程可以簡化,并得出波動方程的解,即波的傳輸形式。
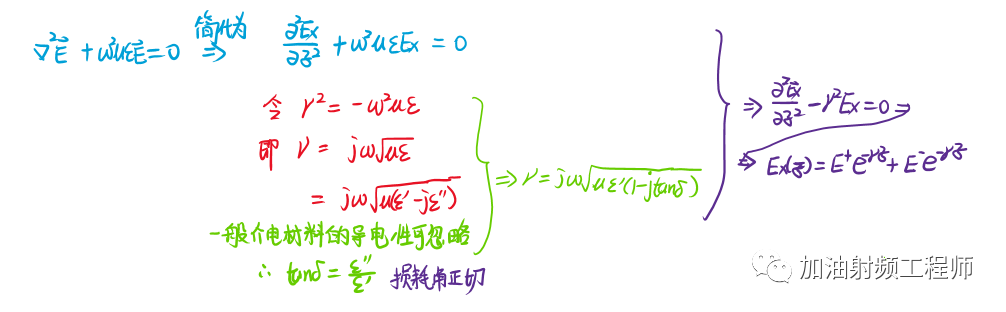
可以看到,因為介電材料中損耗的存在,用損耗角正切來表征,所以波在傳輸過程中,幅度會有衰減,這種衰減,構成了傳輸線的介質損耗。

所以,為了降低傳輸線上的損耗,可以通過選擇損耗角正切小的介電材料。
審核編輯:湯梓紅
-
損耗
+關注
關注
0文章
198瀏覽量
16072 -
傳輸線
+關注
關注
0文章
377瀏覽量
24132 -
衰減
+關注
關注
0文章
31瀏覽量
13525 -
麥克斯韋
+關注
關注
0文章
19瀏覽量
5752
發布評論請先 登錄
相關推薦
麥克斯韋方程組究竟帶來了什么
麥克斯韋Maxwell方程組是怎么來的
淺析麥克斯韋方程組
電磁場理論之麥克斯韋方程組論文的詳細資料免費下載
追逐麥克斯韋方程組與電磁波理論
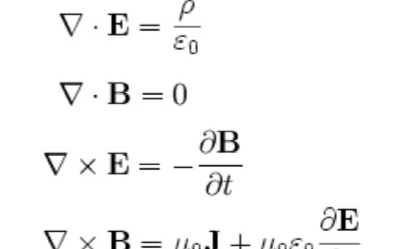
麥克斯韋方程組的詳細資料說明

射頻微波設計入門——麥克斯韋方程組
關于麥克斯韋方程對稱性的報告
描述電磁場的麥克斯韋方程組
深度解析麥克斯韋方程
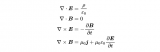




 從麥克斯韋方程看傳輸線中的介質損耗
從麥克斯韋方程看傳輸線中的介質損耗











評論