在本文中，我們將主要介紹Dijkstra算法和A*算法，從成本計(jì)算的角度出發(fā)，并逐步展開討論。

我們將從廣度優(yōu)先搜索開始，然后引入Dijkstra算法，與貪心算法進(jìn)行比較，最終得出A*算法。

成本計(jì)算

在路徑規(guī)劃中，成本計(jì)算的一個主要因素是距離。距離可以作為一種衡量路徑長短的度量指標(biāo)，通常使用歐幾里得距離、曼哈頓距離或其他合適的距離度量方法來計(jì)算。

本文主要介紹歐幾里得距離與曼哈頓距離。

廣度優(yōu)先搜索

廣度優(yōu)先搜索（Breadth First Search，BFS ）是一種圖遍歷算法，按照廣度方向逐層遍歷所有可達(dá)節(jié)點(diǎn)。

BFS的基本思想是通過維護(hù)一個隊(duì)列，逐層訪問節(jié)點(diǎn)。

具體步驟如下：

1、將起始節(jié)點(diǎn)放入隊(duì)列中，并標(biāo)記為已訪問。

2、當(dāng)隊(duì)列非空時，執(zhí)行以下步驟：

從隊(duì)列中取出一個節(jié)點(diǎn)，記為當(dāng)前節(jié)點(diǎn)，并標(biāo)記為已訪問。

如果該節(jié)點(diǎn)是目標(biāo)節(jié)點(diǎn)，則返回結(jié)果。

將當(dāng)前節(jié)點(diǎn)的所有未訪問過的鄰居節(jié)點(diǎn)放入隊(duì)列中。

3、如果隊(duì)列為空，則表示已經(jīng)遍歷完所有可達(dá)節(jié)點(diǎn)，算法結(jié)束。

算法框圖

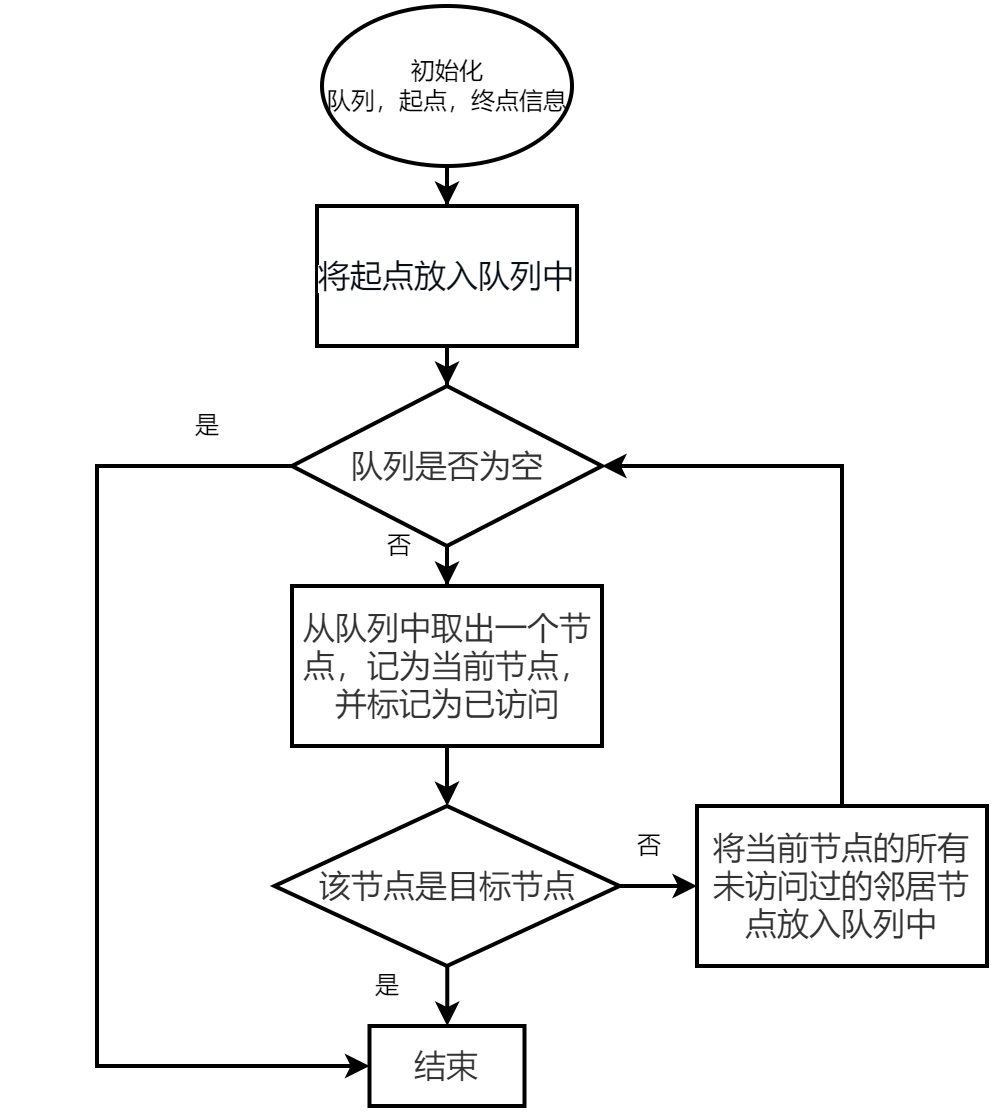
實(shí)現(xiàn)效果如下：

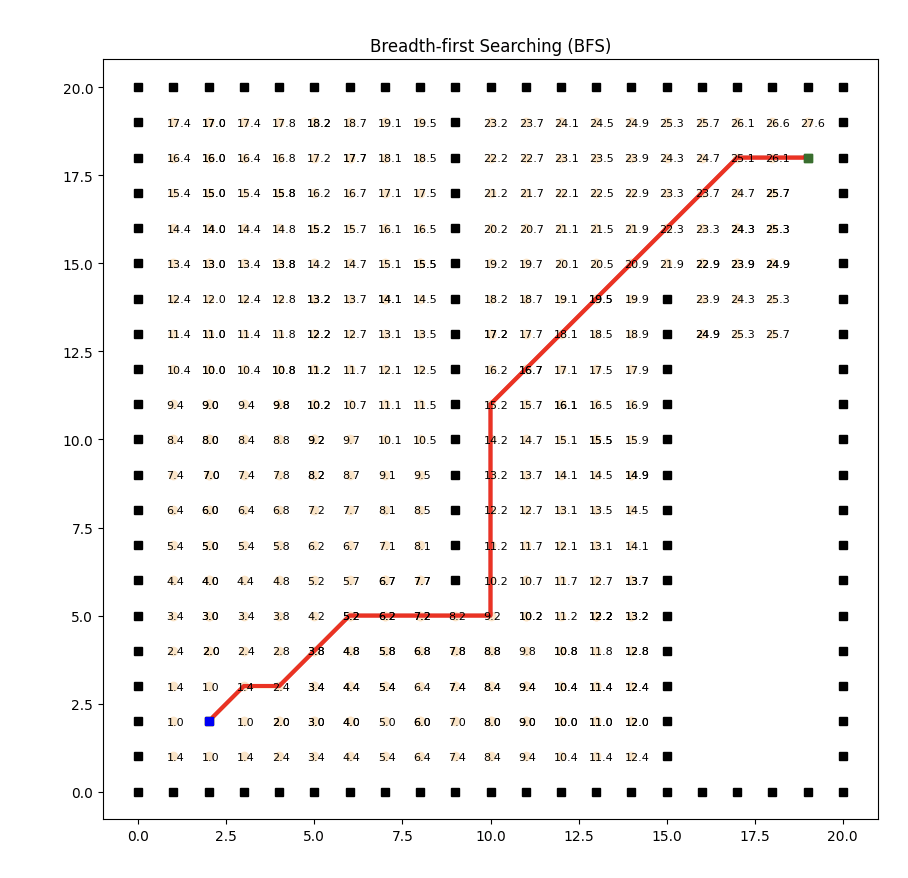
廣度優(yōu)先搜索是一種基本的圖搜索算法，它按照圖的廣度方向逐層遍歷所有可達(dá)節(jié)點(diǎn)。然而，BFS并不考慮邊的權(quán)重，它只關(guān)注節(jié)點(diǎn)的層級關(guān)系。

因此，對于成本計(jì)算來說，BFS并不適用。這里為了實(shí)現(xiàn)到目標(biāo)點(diǎn)的搜索，采用了曼哈頓距離計(jì)算初始點(diǎn)的行進(jìn)成本。

代碼

def searching(self):
  """
    Breadth-first Searching.
     path, visited order
    """


  self.PARENT[self.s_start] = self.s_start # 開始節(jié)點(diǎn)的父節(jié)點(diǎn)
  self.g[self.s_start] = 0 # 開始節(jié)點(diǎn)的成本
  self.g[self.s_goal] = math.inf # 目標(biāo)節(jié)點(diǎn)的成本
  # 統(tǒng)一成本搜索，起點(diǎn)的成本是0
  heapq.heappush(self.OPEN,
          (0, self.s_start))


  while self.OPEN:
    _, s = heapq.heappop(self.OPEN) # 彈出最小的元素，優(yōu)先級較高
    self.CLOSED.append(s) # 將節(jié)點(diǎn)加入被訪問元素隊(duì)列，已訪問


    if s == self.s_goal: # 到達(dá)目標(biāo)點(diǎn)，即停止
      break


      for s_n in self.get_neighbor(s): # 得到s的鄰居節(jié)點(diǎn)
        new_cost = self.g[s] + self.cost(s, s_n) 
        # 計(jì)算當(dāng)前鄰居節(jié)點(diǎn)s_n的成本=g(s)節(jié)點(diǎn)s的成本+s到s_n之間的成本


        if s_n not in self.g: # 當(dāng)前節(jié)點(diǎn)沒有訪問過
          self.g[s_n] = math.inf # 起點(diǎn)到節(jié)點(diǎn)s_n的成本為無窮


          if new_cost < self.g[s_n]: ?# conditions for updating Cost
 ? ? ? ? ? ? ? ? ? ? ? ?self.g[s_n] = new_cost
 ? ? ? ? ? ? ? ? ? ? ? ?self.PARENT[s_n] = s


 ? ? ? ? ? ? ? ? ? ? ? ?# bfs, add new node to the end of the openset
 ? ? ? ? ? ? ? ? ? ? ? ?# 將新的節(jié)點(diǎn)添加到隊(duì)列的末尾
 ? ? ? ? ? ? ? ? ? ? ? ?prior = self.OPEN[-1][0] + 1 if len(self.OPEN) > 0 else 0
            heapq.heappush(self.OPEN, (prior, s_n))
            self.f[s_n] = prior


            return self.extract_path(self.PARENT), self.CLOSED, self.f

Dijkstra算法

迪杰斯特拉算法(Dijkstra)算法是一種單源最短路徑算法，用于在加權(quán)圖中找到從起點(diǎn)到所有其他節(jié)點(diǎn)的最短路徑。

它基于貪心策略，每次選擇當(dāng)前距離起點(diǎn)最近的節(jié)點(diǎn)，并通過該節(jié)點(diǎn)更新與它相鄰的節(jié)點(diǎn)的距離。具體步驟如下：

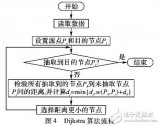
1、初始化：初始化變量和數(shù)據(jù)結(jié)構(gòu)，創(chuàng)建一個包含所有節(jié)點(diǎn)的集合，并為每個節(jié)點(diǎn)設(shè)置一個距離值。將起始節(jié)點(diǎn)的父節(jié)點(diǎn)設(shè)置為自身，將起始節(jié)點(diǎn)的距離值設(shè)置為0，其他節(jié)點(diǎn)的距離值設(shè)置為無窮大（表示尚未找到最短路徑）。將起始節(jié)點(diǎn)以成本0的優(yōu)先級推入優(yōu)先隊(duì)列OPEN中。

2、主循環(huán)：當(dāng)OPEN非空時：

彈出優(yōu)先級最小（成本最低）的節(jié)點(diǎn)(_, s)，其中_為忽略的值，s為當(dāng)前節(jié)點(diǎn)。

將當(dāng)前節(jié)點(diǎn)s添加到CLOSED列表中，表示已訪問。

檢查當(dāng)前節(jié)點(diǎn)是否為目標(biāo)節(jié)點(diǎn)。如果是，則跳出循環(huán)。

對于當(dāng)前節(jié)點(diǎn)的所有鄰居節(jié)點(diǎn)，計(jì)算通過當(dāng)前節(jié)點(diǎn)到達(dá)鄰居節(jié)點(diǎn)的距離，并與鄰居節(jié)點(diǎn)的當(dāng)前距離值進(jìn)行比較。

如果計(jì)算得到的距離值小于鄰居節(jié)點(diǎn)的當(dāng)前距離值，則更新鄰居節(jié)點(diǎn)的距離值為新的更小值并將鄰居節(jié)點(diǎn)s_n以新的成本作為優(yōu)先級推入優(yōu)先隊(duì)列OPEN中循環(huán)結(jié)束后，可以通過從目標(biāo)節(jié)點(diǎn)回溯到起始節(jié)點(diǎn)，在PARENT字典中提取最短路徑。

3、循環(huán)結(jié)束后，可以通過從目標(biāo)節(jié)點(diǎn)回溯到起始節(jié)點(diǎn)，在PARENT字典中提取最短路徑。

算法框圖

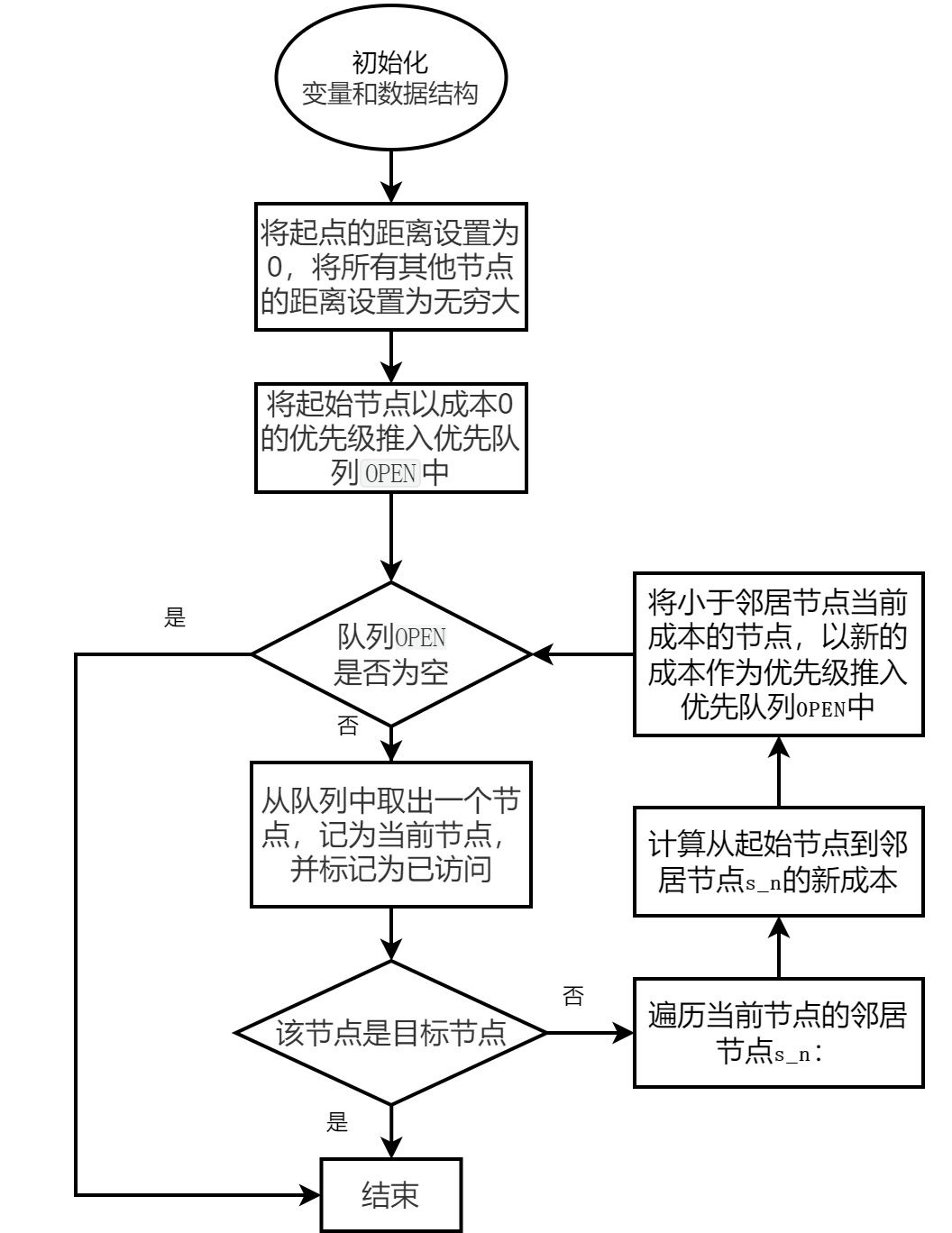
實(shí)現(xiàn)效果如下：

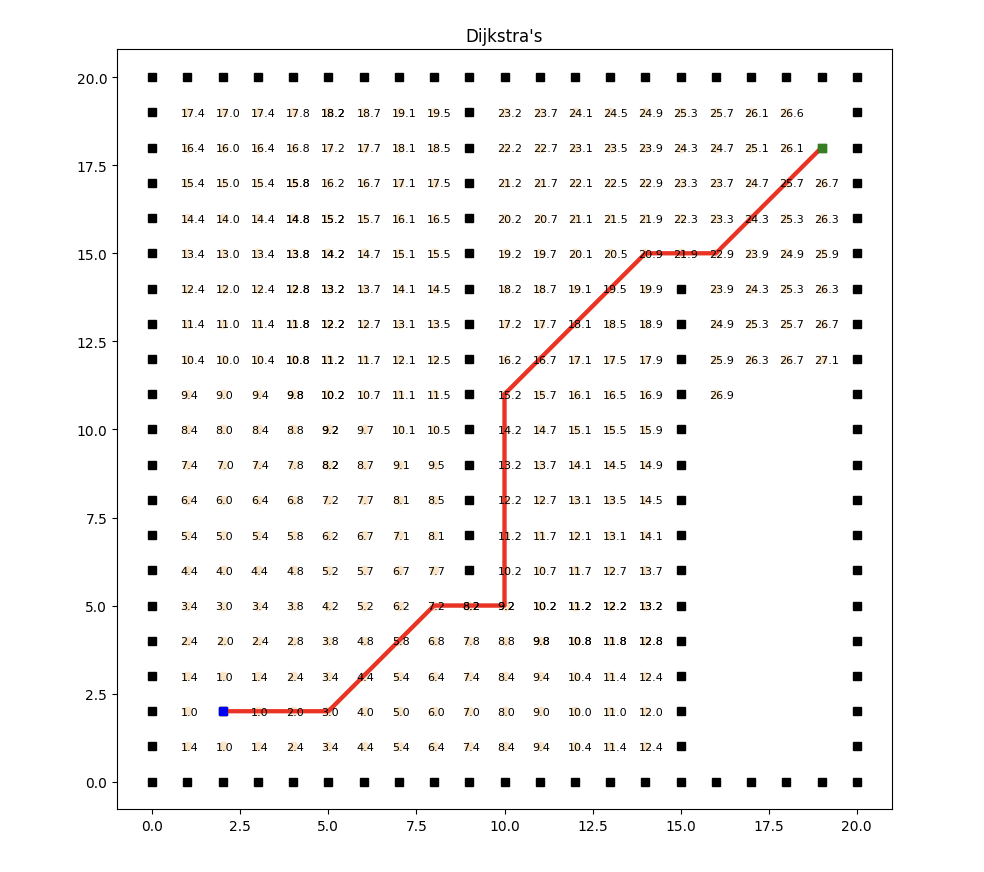
Dijkstra算法能夠正確地找到起始節(jié)點(diǎn)到其他所有節(jié)點(diǎn)的最短路徑。它基于貪婪策略，每次選擇當(dāng)前最短路徑的節(jié)點(diǎn)，通過逐步更新節(jié)點(diǎn)的距離值，最終找到最短路徑。

代碼

  def searching(self):
    """
    Breadth-first Searching.
     path, visited order
    """


    self.PARENT[self.s_start] = self.s_start # 開始節(jié)點(diǎn)的父節(jié)點(diǎn)
    self.g[self.s_start] = 0 # 開始節(jié)點(diǎn)的成本
    self.g[self.s_goal] = math.inf # 目標(biāo)節(jié)點(diǎn)的成本


    # 統(tǒng)一成本搜索，起點(diǎn)的成本是0
    heapq.heappush(self.OPEN,
            (0, self.s_start))


    while self.OPEN: # open_list
      _, s = heapq.heappop(self.OPEN) # 彈出最小的元素，優(yōu)先級較高
      self.CLOSED.append(s) # 將節(jié)點(diǎn)加入被訪問元素隊(duì)列


      if s == self.s_goal: # 到達(dá)目標(biāo)點(diǎn)，即停止
        break


      for s_n in self.get_neighbor(s): # 得到s的鄰居節(jié)點(diǎn)
        new_cost = self.g[s] + self.cost(s, s_n) # 計(jì)算當(dāng)時鄰居節(jié)點(diǎn)s_n的成本=g(s)節(jié)點(diǎn)s的成本+s到s_n之間的成本


        if s_n not in self.g:  # 當(dāng)前節(jié)點(diǎn)沒有訪問過
          self.g[s_n] = math.inf # 起點(diǎn)到節(jié)點(diǎn)s_n的成本為無窮


        if new_cost < self.g[s_n]: ?# 預(yù)估節(jié)點(diǎn)s_n成本

	

	貪婪算法

	貪婪算法（Greedy Algorithm）是一種常見的算法設(shè)計(jì)策略，其基本思想是在每一步選擇當(dāng)前最優(yōu)解，而不考慮整體的最優(yōu)解。貪婪算法通常以局部最優(yōu)解為目標(biāo)，通過不斷做出局部最優(yōu)選擇來達(dá)到整體最優(yōu)解。

	貪婪算法在路徑規(guī)劃問題中，根據(jù)當(dāng)前位置到目標(biāo)位置的成本作為啟發(fā)式評估準(zhǔn)則，選擇最近的節(jié)點(diǎn)作為下一步移動的目標(biāo)。具體步驟如下：

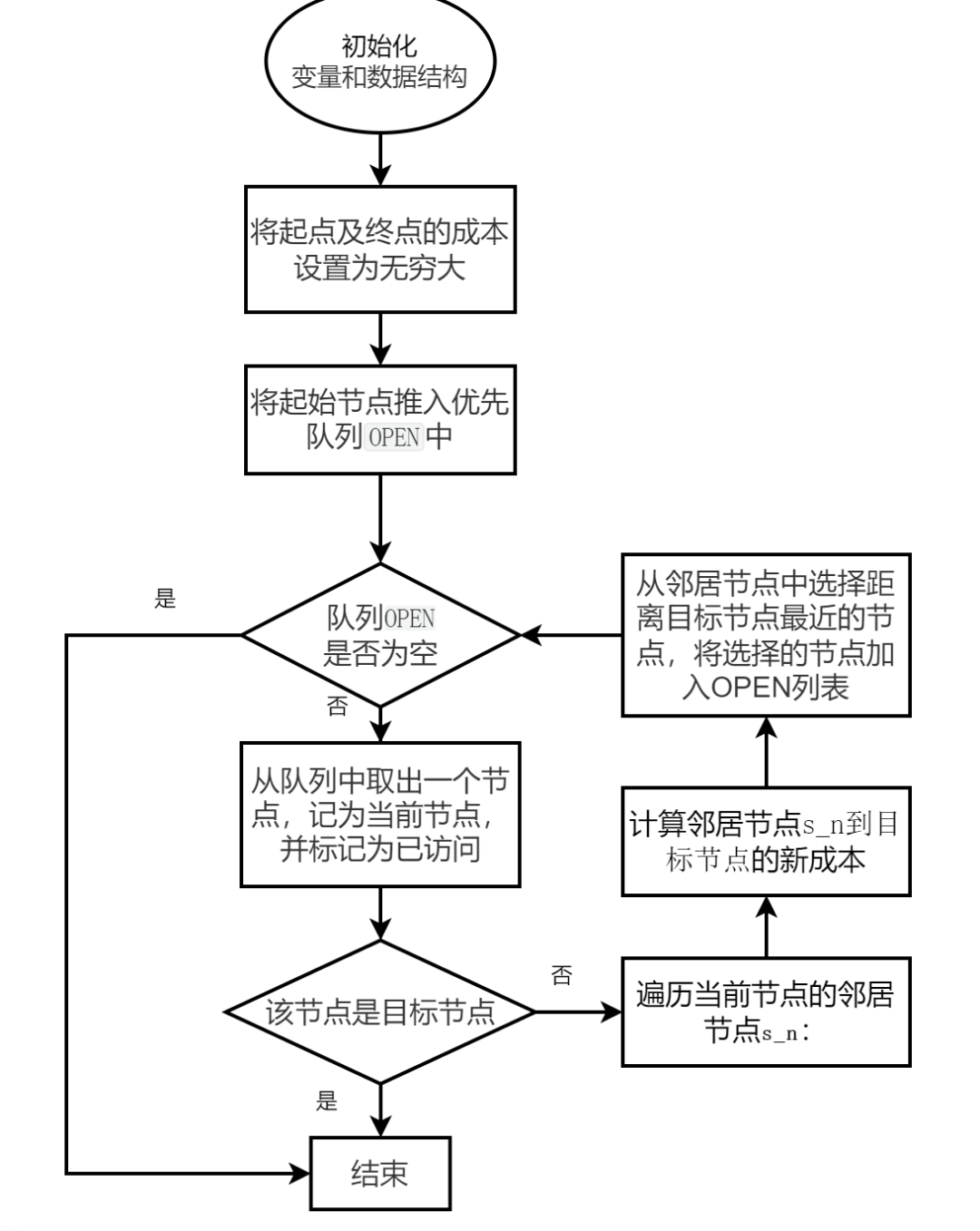
	1、初始化：設(shè)置起始節(jié)點(diǎn)，將起始節(jié)點(diǎn)的父節(jié)點(diǎn)設(shè)置為起始節(jié)點(diǎn)本身，并將起始節(jié)點(diǎn)和目標(biāo)節(jié)點(diǎn)的成本初始化為無窮大，將起始節(jié)點(diǎn)加入開放列表，其優(yōu)先級根據(jù)啟發(fā)式函數(shù)值確定。

	2、主循環(huán)：當(dāng)OPEN非空時：

	從OPEN列表中彈出具有最高優(yōu)先級的節(jié)點(diǎn)，將其加入已訪問列表（CLOSED）中。

	檢查當(dāng)前節(jié)點(diǎn)是否為目標(biāo)節(jié)點(diǎn)。如果是，則跳出循環(huán)。

	獲取當(dāng)前節(jié)點(diǎn)的鄰居節(jié)點(diǎn)，從鄰居節(jié)點(diǎn)中選擇距離目標(biāo)節(jié)點(diǎn)最近的節(jié)點(diǎn)，將選擇的節(jié)點(diǎn)加入OPEN列表，并將該節(jié)點(diǎn)作為當(dāng)前節(jié)點(diǎn)。

	3、循環(huán)結(jié)束后，通過從目標(biāo)節(jié)點(diǎn)回溯到起始節(jié)點(diǎn)，在PARENT字典中提取最短路徑。

	算法框圖

	

	實(shí)現(xiàn)效果如下：

	

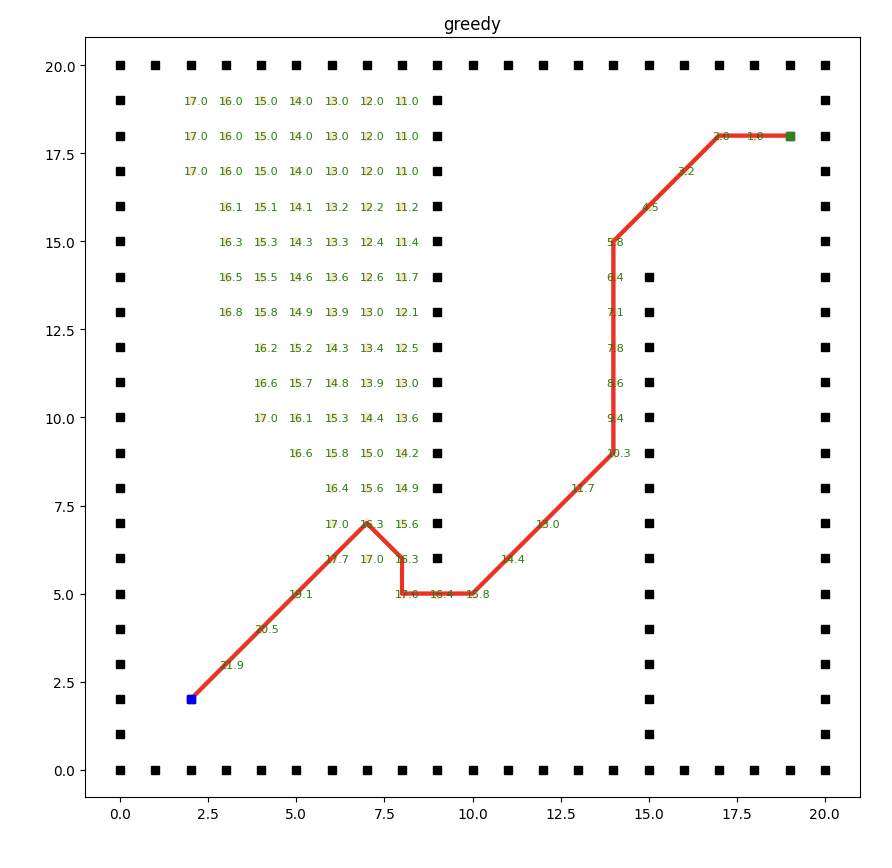
	貪婪最佳優(yōu)先搜索算法的局限性在于它過度依賴啟發(fā)式函數(shù)（heuristic function），該函數(shù)用于估計(jì)節(jié)點(diǎn)到目標(biāo)節(jié)點(diǎn)的距離。

	由于啟發(fā)式函數(shù)的估計(jì)可能不準(zhǔn)確或不全面，算法可能會在搜索過程中陷入局部最優(yōu)解，導(dǎo)致得到的路徑并不是最短的。

	代碼

	
 def searching(self):
    self.PARENT[self.s_start] = self.s_start # 開始節(jié)點(diǎn)的父節(jié)點(diǎn)
    self.h[self.s_start] = math.inf # 開始節(jié)點(diǎn)的成本
    self.h[self.s_goal] = math.inf # 目標(biāo)節(jié)點(diǎn)的成本
    # heappush 函數(shù)能夠按照 h 值的大小來維護(hù)堆的順序，這意味著self.OPEN堆中的節(jié)點(diǎn)將按照 h 值的升序排列，h 值較小的節(jié)點(diǎn)將具有較高的優(yōu)先級。
    heapq.heappush(self.OPEN,
            (self.heuristic(self.s_start), self.s_start))


    while self.OPEN: # 當(dāng)不為空時，即存在未探索區(qū)域
      _, s = heapq.heappop(self.OPEN) # 彈出最小的元素，優(yōu)先級較高
      self.CLOSED.append(s) # 將節(jié)點(diǎn)加入被訪問元素隊(duì)列


      if s == self.s_goal: # stop condition，到達(dá)目標(biāo)點(diǎn)，即停止
        break
      for s_n in self.get_neighbor(s): # 得到s的鄰居節(jié)點(diǎn)
        new_cost = self.heuristic(s_n) + self.cost(s, s_n) # 計(jì)算當(dāng)時鄰居節(jié)點(diǎn)s_n的成本=g(s)節(jié)點(diǎn)s的成本+s到s_n之間的成本


        if s_n not in self.h: # 下一個節(jié)點(diǎn)沒有遍歷過
          self.h[s_n] = math.inf # 起點(diǎn)到節(jié)點(diǎn)s_n的成本為無窮


        if new_cost < self.h[s_n]: ?# 預(yù)估節(jié)點(diǎn)s_n成本

	

	A*算法

	Dijkstra算法沒有考慮到目標(biāo)節(jié)點(diǎn)的位置，因此可能會浪費(fèi)時間在探索那些與目標(biāo)節(jié)點(diǎn)相距較遠(yuǎn)的方向上。貪婪最佳優(yōu)先搜索算法會優(yōu)先選擇離目標(biāo)節(jié)點(diǎn)更近的節(jié)點(diǎn)進(jìn)行擴(kuò)展。

	這樣做的好處是它能夠更快地找到到達(dá)目標(biāo)節(jié)點(diǎn)的路徑，但無法保證找到的路徑是最短路徑，因?yàn)樗豢紤]了節(jié)點(diǎn)到目標(biāo)節(jié)點(diǎn)的距離，沒有綜合考慮到起點(diǎn)到目標(biāo)節(jié)點(diǎn)的實(shí)際距離。

	A*算法是一種綜合了Dijkstra算法和貪婪最佳優(yōu)先搜索的啟發(fā)式搜索算法。A*算法同時使用了節(jié)點(diǎn)到起點(diǎn)的實(shí)際距離（表示為g值）和節(jié)點(diǎn)到目標(biāo)節(jié)點(diǎn)的估計(jì)距離（表示為h值）。

	它通過綜合考慮這兩個值來評估節(jié)點(diǎn)的優(yōu)先級，并選擇優(yōu)先級最高的節(jié)點(diǎn)進(jìn)行擴(kuò)展。

	A算法通過選擇合適的啟發(fā)式函數(shù)來平衡搜索的速度和路徑的優(yōu)劣。當(dāng)啟發(fā)式函數(shù)滿足一定條件時，A算法能夠保證找到最短路徑。

	Dijkstra與貪婪搜索算法對比

	在路徑規(guī)劃中，貪婪算法關(guān)注的是當(dāng)前節(jié)點(diǎn)到目標(biāo)節(jié)點(diǎn)的距離（啟發(fā)式函數(shù)值），它傾向于選擇離目標(biāo)節(jié)點(diǎn)最近的節(jié)點(diǎn)作為下一步。

	Dijkstra算法關(guān)注的是從起點(diǎn)到各個節(jié)點(diǎn)的距離，通過不斷更新節(jié)點(diǎn)的最短距離來逐步擴(kuò)展路徑。

	

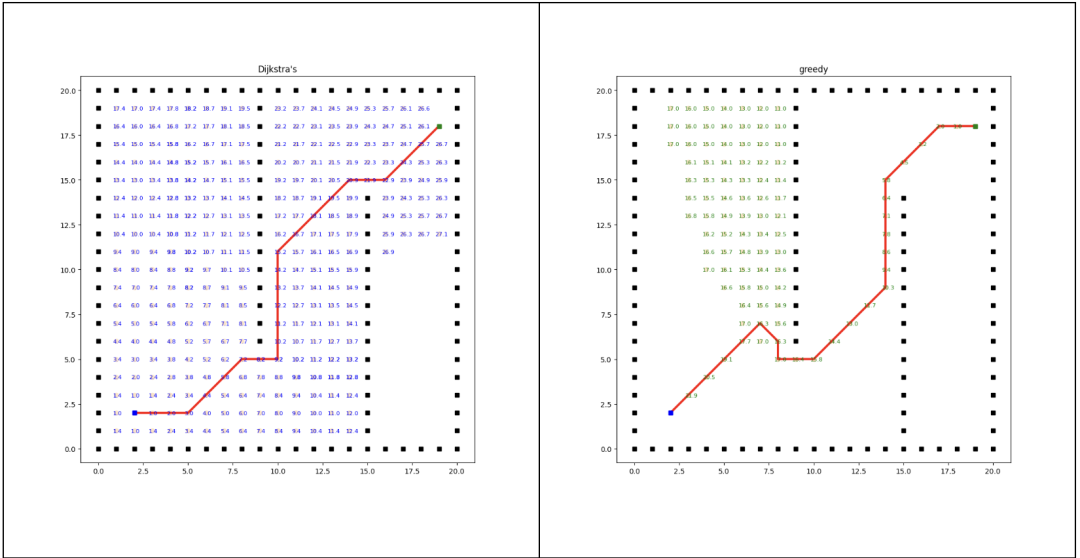
	A*算法的成本函數(shù)是由兩部分組成：g(n)和h(n)。

	g(n)表示從起點(diǎn)到達(dá)節(jié)點(diǎn)n的實(shí)際距離（也稱為已知最短路徑的代價(jià)），表示為g(n)。——Dijkstra

	h(n)表示從節(jié)點(diǎn)n到目標(biāo)節(jié)點(diǎn)的預(yù)估距離（也稱為啟發(fā)式函數(shù)），表示為h(n)。——貪婪搜索

	A算法使用這兩個值來評估節(jié)點(diǎn)的優(yōu)先級。具體地，A算法為每個節(jié)點(diǎn)計(jì)算一個估計(jì)總代價(jià)f(n)，計(jì)算公式為：

	

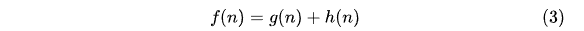
	其中，f(n)表示從起點(diǎn)經(jīng)過節(jié)點(diǎn)n到達(dá)目標(biāo)節(jié)點(diǎn)的預(yù)估總代價(jià)。

	

	具體步驟如下：

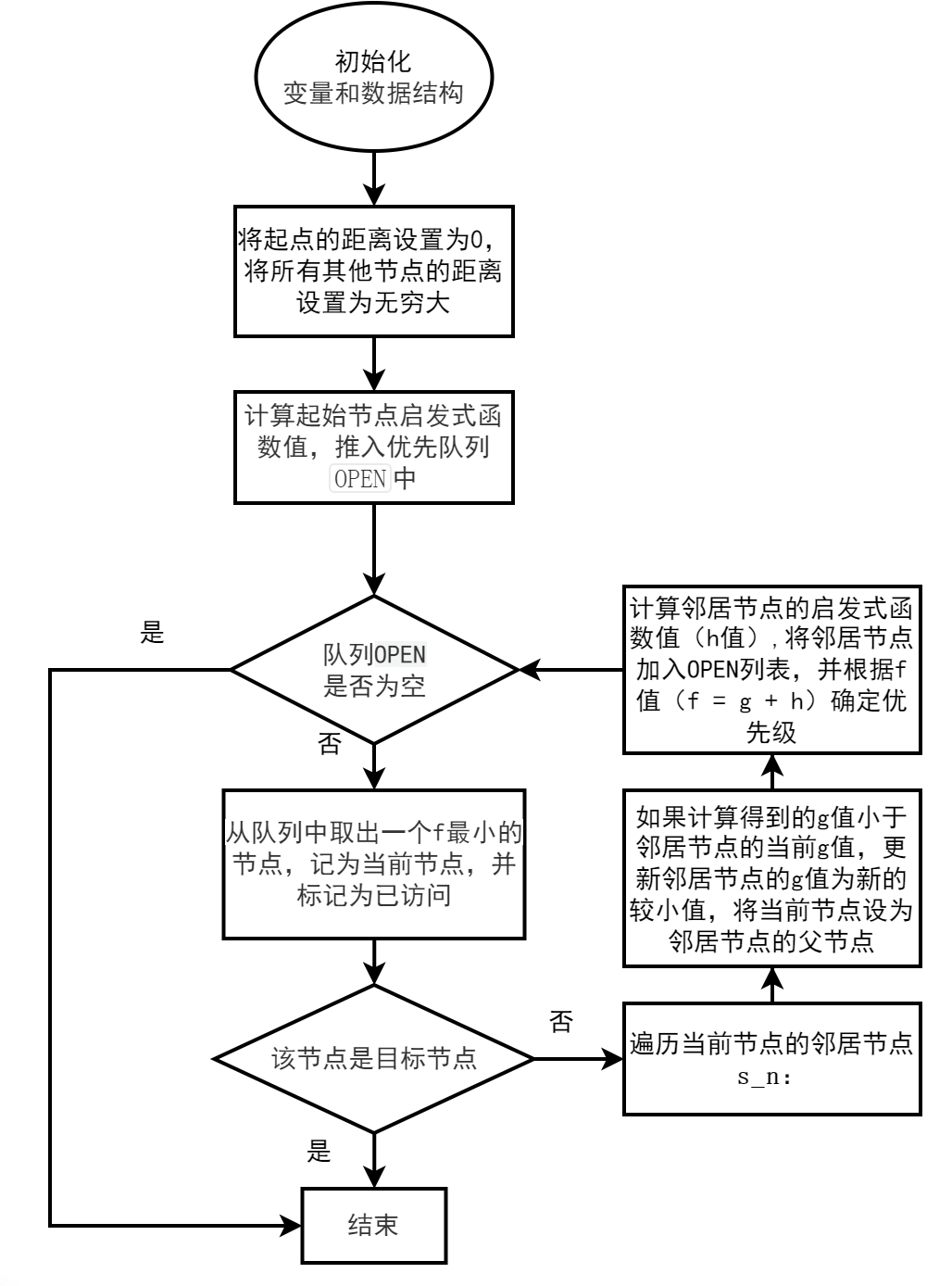
	1、初始化：設(shè)置起始節(jié)點(diǎn)，將起始節(jié)點(diǎn)的父節(jié)點(diǎn)設(shè)置為起始節(jié)點(diǎn)本身，將起始節(jié)點(diǎn)的成本設(shè)置為0，將目標(biāo)節(jié)點(diǎn)的成本設(shè)置為無窮大，將起始節(jié)點(diǎn)加入到OPEN列表中，使用節(jié)點(diǎn)的f值作為優(yōu)先級。

	2、主循環(huán)：當(dāng)OPEN非空時：

	從OPEN列表中彈出具有最高優(yōu)先級的節(jié)點(diǎn)，將其加入已訪問列表（CLOSED）中。 

	檢查當(dāng)前節(jié)點(diǎn)是否為目標(biāo)節(jié)點(diǎn)。如果是，則跳出循環(huán)。 

	獲取當(dāng)前節(jié)點(diǎn)的鄰居節(jié)點(diǎn)。

	 對于每個鄰居節(jié)點(diǎn)，執(zhí)行以下步驟：

	計(jì)算從起始節(jié)點(diǎn)經(jīng)過當(dāng)前節(jié)點(diǎn)到達(dá)鄰居節(jié)點(diǎn)的實(shí)際距離，即g值。 

	如果鄰居節(jié)點(diǎn)不在g字典中，將其g值初始化為無窮大。 

	如果計(jì)算得到的g值小于鄰居節(jié)點(diǎn)的當(dāng)前g值，更新鄰居節(jié)點(diǎn)的g值為新的更小值，并將當(dāng)前節(jié)點(diǎn)設(shè)為鄰居節(jié)點(diǎn)的父節(jié)點(diǎn)。 

	計(jì)算鄰居節(jié)點(diǎn)的啟發(fā)式函數(shù)值，即h值。 

	將鄰居節(jié)點(diǎn)加入OPEN列表，并根據(jù)f值（f = g + h）確定其優(yōu)先級。

	3、循環(huán)結(jié)束后，通過從目標(biāo)節(jié)點(diǎn)回溯到起始節(jié)點(diǎn)，在PARENT字典中提取最短路徑。

	算法框圖

	

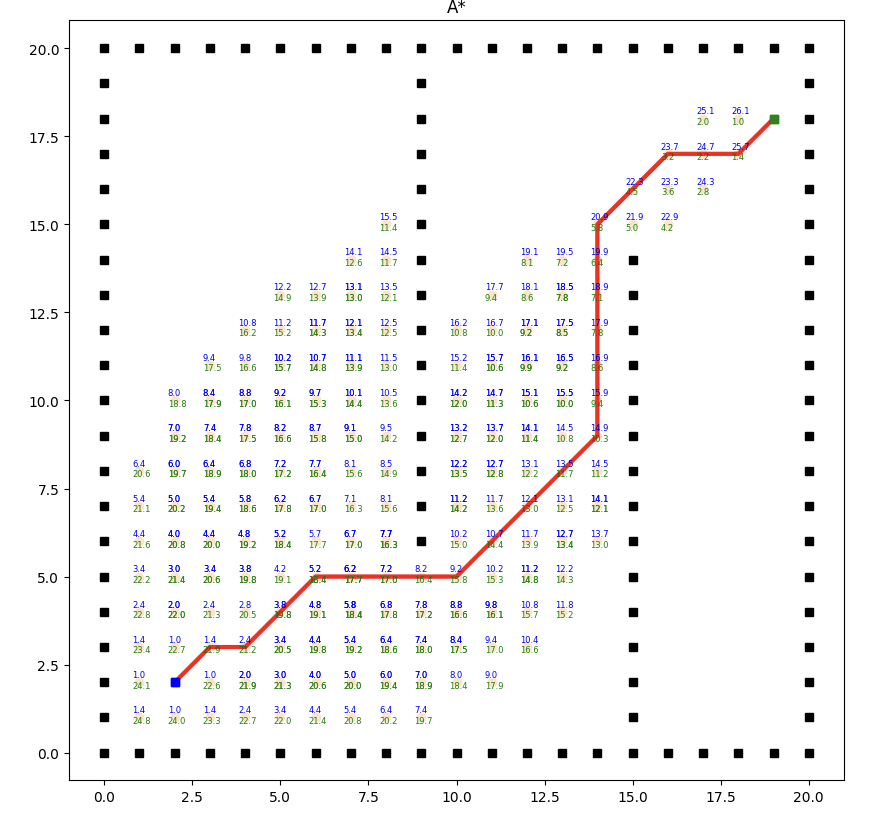
	實(shí)現(xiàn)效果如下：

	

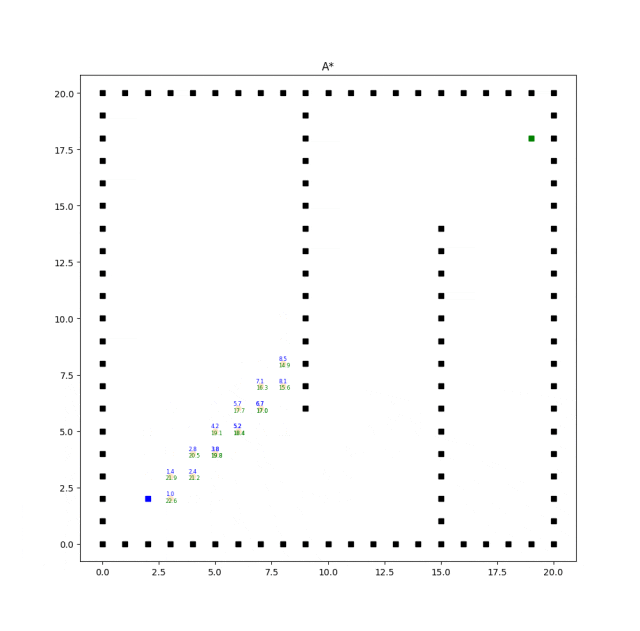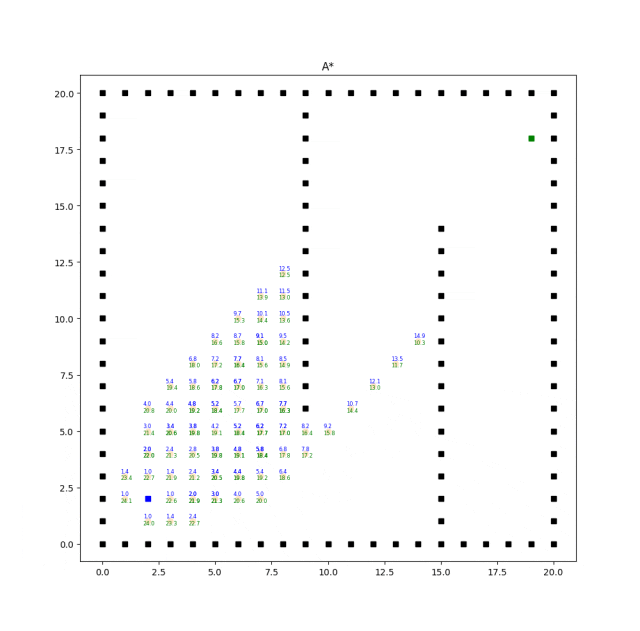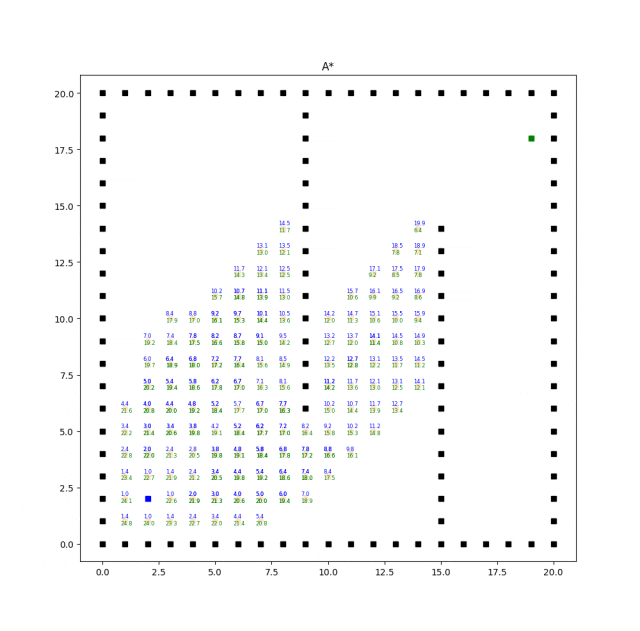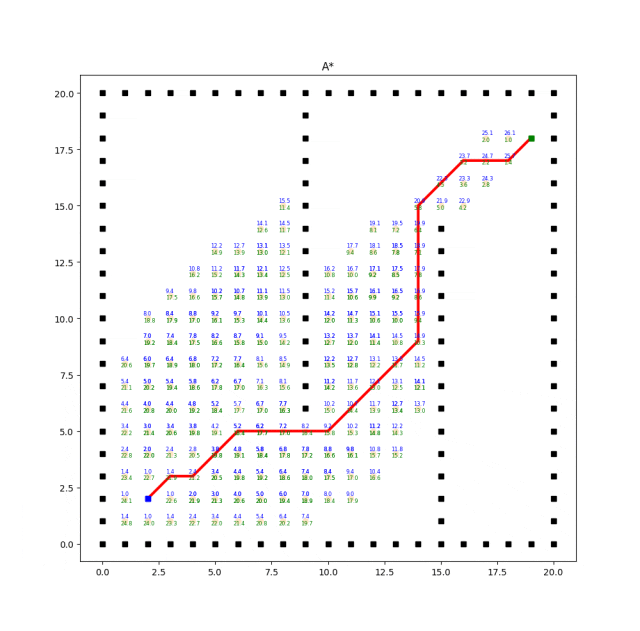
	A*算法的效率和質(zhì)量受啟發(fā)式函數(shù)的選擇影響較大。合理選擇啟發(fā)式函數(shù)能夠提供更好的搜索引導(dǎo)，但不同問題可能需要設(shè)計(jì)不同的啟發(fā)式函數(shù)。

	代碼

	
def searching(self):
    """
    A_star Searching.
     path, visited order
    """


    self.PARENT[self.s_start] = self.s_start # 開始節(jié)點(diǎn)的父節(jié)點(diǎn)
    self.g[self.s_start] = 0 # 開始節(jié)點(diǎn)的成本
    self.g[self.s_goal] = math.inf # 目標(biāo)節(jié)點(diǎn)的成本


    # heappush 函數(shù)能夠按照 f 值的大小來維護(hù)堆的順序，這意味著self.OPEN堆中的節(jié)點(diǎn)將按照 f 值的升序排列，f 值較小的節(jié)點(diǎn)將具有較高的優(yōu)先級。
    heapq.heappush(self.OPEN,
            (self.f_value(self.s_start), self.s_start))


    while self.OPEN: # 當(dāng)不為空時，即存在未探索區(qū)域
      _, s = heapq.heappop(self.OPEN) # 彈出最小的元素，優(yōu)先級較高
      self.CLOSED.append(s) # 將節(jié)點(diǎn)加入被訪問元素隊(duì)列


      if s == self.s_goal: # stop condition，到達(dá)目標(biāo)點(diǎn)，即停止
        break
      for s_n in self.get_neighbor(s): # 得到s的鄰居節(jié)點(diǎn)
        new_cost = self.g[s] + self.cost(s, s_n) # 計(jì)算當(dāng)時鄰居節(jié)點(diǎn)s_n的成本=g(s)節(jié)點(diǎn)s的成本+s到s_n之間的成本


        if s_n not in self.g:
          self.g[s_n] = math.inf # 起點(diǎn)到節(jié)點(diǎn)s_n的成本為無窮


        if new_cost < self.g[s_n]: ?# 預(yù)估節(jié)點(diǎn)s_n成本