機(jī)器學(xué)習(xí)和深度學(xué)習(xí)中的模型都是遵循數(shù)學(xué)函數(shù)的方式創(chuàng)建的。從數(shù)據(jù)分析到預(yù)測(cè)建模，一般情況下都會(huì)有數(shù)學(xué)原理的支撐，比如：歐幾里得距離用于檢測(cè)聚類中的聚類。

傅里葉變換是一種眾所周知的將函數(shù)從一個(gè)域轉(zhuǎn)換到另一個(gè)域的數(shù)學(xué)方法，它也可以應(yīng)用于深度學(xué)習(xí)。

本文將討論傅里葉變換，以及如何將其用于深度學(xué)習(xí)領(lǐng)域。

什么是傅里葉變換？

在數(shù)學(xué)中，變換技術(shù)用于將函數(shù)映射到與其原始函數(shù)空間不同的函數(shù)空間。傅里葉變換時(shí)也是一種變換技術(shù)，它可以將函數(shù)從時(shí)域空間轉(zhuǎn)換到頻域空間。例如以音頻波為例，傅里葉變換可以根據(jù)其音符的音量和頻率來表示它。

我們可以說，任何函數(shù)的傅里葉變換所執(zhí)行的變換都是頻率的函數(shù)。其中結(jié)果函數(shù)的大小是原始函數(shù)所包含的頻率的表示。

我們舉一個(gè)信號(hào)的例子，它的時(shí)域函數(shù)如下所示：

在同一時(shí)間范圍內(nèi)獲取另一個(gè)信號(hào)的一部分：

將這兩個(gè)信號(hào)的稱為和，其中 n 是時(shí)域。因此，如果我們添加這些信號(hào)，信號(hào)的結(jié)構(gòu)將如下所示：

可以看到，函數(shù)的信號(hào)相加是將兩個(gè)信號(hào)進(jìn)行了加的操作，如果我們?cè)噲D從這個(gè)相加信號(hào) C 中提取信號(hào) A 或 B，我們會(huì)遇到一個(gè)問題，因?yàn)?這些信號(hào)只是功率相加，和時(shí)間沒有關(guān)系。也就是說相加的操作是同一時(shí)間上的功率的相加。

可以在上圖中看到，頻域可以很容易地突出信號(hào)之間的差異。如果希望將這些信號(hào)轉(zhuǎn)換回時(shí)域，我們可以使用傅里葉逆變換。

傅立葉變數(shù)學(xué)原理

正弦序列可用于表示時(shí)域中的信號(hào)，這是傅立葉變換的基礎(chǔ)。所以如果函數(shù)是一個(gè)連續(xù)信號(hào)，函數(shù)f可以用來表示為：

可以看到該函數(shù)是由無限正弦曲線相加組成的，我們可以將其視為函數(shù)信號(hào)的表示，并且該函數(shù)具有定義輸出信號(hào)結(jié)構(gòu)所需的兩個(gè)系數(shù)。

求解傅里葉變換積分（本質(zhì)上是頻率的函數(shù)）會(huì)產(chǎn)生這些系數(shù)。傅里葉變換的結(jié)果可以被認(rèn)為是一組系數(shù)。它可以用數(shù)學(xué)表示如下：

而這個(gè)函數(shù)的倒數(shù)可以看作是我們用來將頻域函數(shù)轉(zhuǎn)換為時(shí)域函數(shù)的時(shí)間函數(shù)，也就是傅里葉逆變換。

求解上面的這些積分可以得到a和b的值，這里討論的是信號(hào)是連續(xù)信號(hào)的情況。但是在現(xiàn)實(shí)生活中，大多數(shù)問題都是從離散采樣的信號(hào)中產(chǎn)生的，為了找出這種信號(hào)變換的系數(shù)，我們需要執(zhí)行離散傅里葉變換 (DFT)。

使用DFT我們可以得到一個(gè)相同長(zhǎng)度等間隔的樣本序列，這個(gè)函數(shù)是由一組等間隔的樣本序列組成的。上面給出的函數(shù)的系數(shù)可以由下面的函數(shù)得到。

和的值將是:

在函數(shù)中使用項(xiàng)和，就可以找到頻域中的信號(hào)。

使用 Python 進(jìn)行傅里葉變換

Python 的 scipy 模塊提供了數(shù)學(xué)中所需的所有轉(zhuǎn)換技術(shù)，所以可以直接使用它

import numpy as np 
import matplotlib.pyplot as plt 
from scipy.fft import fft, fftfreq

制作正弦波

#  sample points 
N = 1200 
 
# sample spacing 
T = 1.0 / 1600.0 
 
x = np.linspace(0.0, N*T, N, endpoint=False) 
sum = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x) 
 
plt.plot(sum) 
plt.title('Sine wave') 
plt.xlabel('Time') 
plt.ylabel('Amplitude') 
plt.grid(True, which='both') 
plt.show()

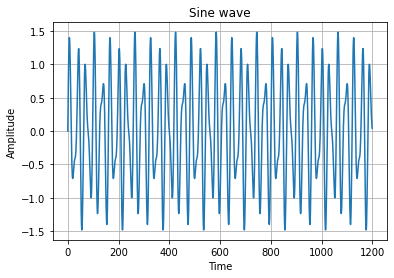
上面的輸出中，可以看到使用 NumPy 生成的正弦波，現(xiàn)在可以使用 scipy 庫的 FFT 模塊對(duì)其進(jìn)行轉(zhuǎn)換。

sumf = fft(sum) 
xf = fftfreq(N, T)[:N//2] 
plt.ylabel('frequency') 
plt.xlabel('sample') 
plt.title("FFT of sum of two sines") 
plt.plot(xf, 2.0/N * np.abs(sumf[0:N//2])) 
plt.show()

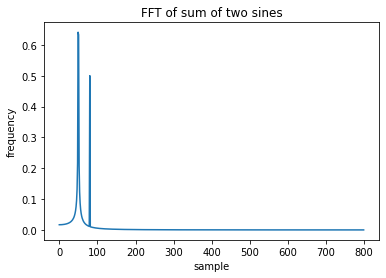
現(xiàn)在可以清楚地看到各種波的頻率是多少，作為時(shí)域的函數(shù)形成的時(shí)這些并不明顯，只有在頻域表示時(shí)才能清楚的看到這些區(qū)別。

通過上面的介紹已經(jīng)了解了傅立葉變換的基本內(nèi)容，但它現(xiàn)在與神經(jīng)網(wǎng)絡(luò)有什么關(guān)系呢？傅里葉變換是一種逼近其他頻域函數(shù)的工具，而神經(jīng)網(wǎng)絡(luò)也可以逼近任意函數(shù)。我們將在本文的下一部分中介紹神經(jīng)網(wǎng)絡(luò)和傅里葉變換之間的關(guān)系。

神經(jīng)網(wǎng)絡(luò)和傅里葉變換之間有什么關(guān)系？

可以將傅里葉變換視為一種有助于逼近其他函數(shù)的函數(shù)，并且我們還知道神經(jīng)網(wǎng)絡(luò)可以被認(rèn)為是一種函數(shù)逼近技術(shù)或通用函數(shù)逼近技術(shù)。

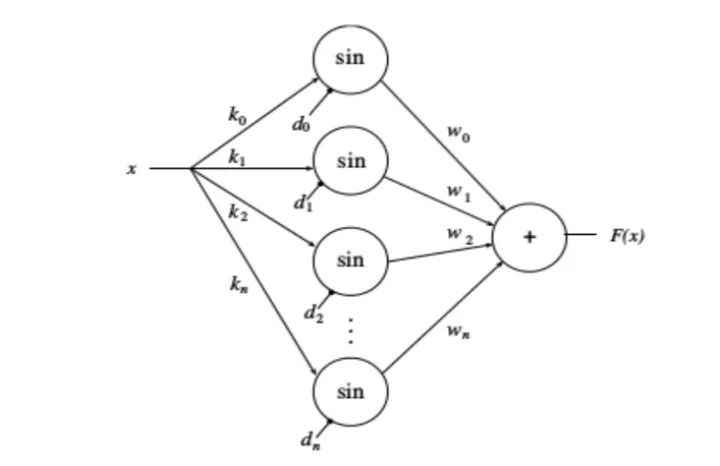
上圖描繪了一個(gè)采用傅里葉變換方法的神經(jīng)網(wǎng)絡(luò)。一個(gè)相對(duì)基本的神經(jīng)網(wǎng)絡(luò)的目標(biāo)是希望在特定時(shí)間逼近一個(gè)未知函數(shù)及其值。大多數(shù)神經(jīng)網(wǎng)絡(luò)的任務(wù)是學(xué)習(xí)整個(gè)函數(shù)或算法或數(shù)據(jù)中指定的值點(diǎn)處的函數(shù)，傅里葉網(wǎng)絡(luò)也是一樣通過迭代技術(shù)找到逼近函數(shù)的參數(shù)。

卷積神經(jīng)網(wǎng)絡(luò)中的傅立葉變換

卷積神經(jīng)網(wǎng)絡(luò)中卷積層是主要基礎(chǔ)組曾，在網(wǎng)絡(luò)中，任何卷積層的主要工作是將濾波器（卷積核）應(yīng)用于輸入數(shù)據(jù)或特征圖，對(duì)前一層的輸出進(jìn)行卷積。該層的任務(wù)是學(xué)習(xí)過濾器的權(quán)重。在一個(gè)復(fù)雜的卷積神經(jīng)網(wǎng)絡(luò)中看到，層數(shù)很多，每層的過濾器也很多，這使得計(jì)算成本非常高。

使用傅里葉變換可以將層計(jì)算轉(zhuǎn)換為頻域中的元素乘積，網(wǎng)絡(luò)的任務(wù)將是相同的，但是可以通過使用傅里葉變換來節(jié)省計(jì)算器的能量。

綜上所述，我們可以說卷積層或卷積層的過程與傅里葉變換有關(guān)。大多數(shù)時(shí)域中的卷積層可以被認(rèn)為是頻域中的乘法。我們可以很容易地通過多項(xiàng)式乘法來理解卷積。

假設(shè)我們必須對(duì)任意值的和進(jìn)行函數(shù)處理，如下所示：

而這些函數(shù)的多項(xiàng)式乘法可以寫成函數(shù)h

綜上所述，我們可以說卷積層過程可以定義為上述給定函數(shù)的乘積。函數(shù)的向量形式可以寫成：

向量形式的向量乘法為：

其中：

乘法中的符號(hào)“.”表示乘法，是卷積的。

和分別是傅里葉變換和傅里葉逆變換。

“”和“”分別是時(shí)域和頻域。

綜上所述，我們可以看到如果函數(shù)與時(shí)域相關(guān)，卷積層最終意味著傅里葉變換及其在乘法中的逆。

如何在深度學(xué)習(xí)中使用傅立葉變換？

在上一節(jié)中，我們已經(jīng)看到時(shí)域中的卷積過程可以簡(jiǎn)單地認(rèn)為是頻域中的乘法。這證明它可以用于各種深度學(xué)習(xí)算法，即使它可以用于各種靜態(tài)預(yù)測(cè)建模算法。

我們來看一個(gè)類似的卷積神經(jīng)網(wǎng)絡(luò)示例，這樣我們就不會(huì)偏離本文的主題。

卷積數(shù)學(xué)操作是在時(shí)域中執(zhí)行乘法，而傅里葉變換背后的數(shù)學(xué)是在頻域中進(jìn)行乘法。

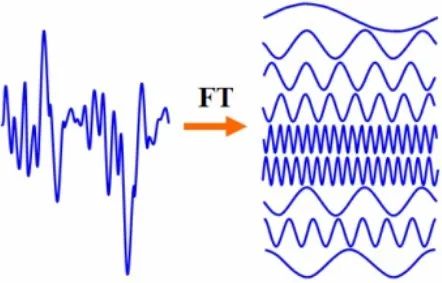
為了在任何卷積神經(jīng)網(wǎng)絡(luò)中應(yīng)用傅里葉變換，我們可以對(duì)輸入和濾波器進(jìn)行一些更改。

如果 CNN 中的輸入矩陣和濾波器矩陣可以轉(zhuǎn)換為頻域進(jìn)行乘法運(yùn)算，并且頻域乘法的結(jié)果矩陣可以轉(zhuǎn)換為時(shí)域矩陣，則不會(huì)對(duì)算法的準(zhǔn)確性造成任何影響。矩陣從時(shí)域到頻域的轉(zhuǎn)換可以通過傅里葉變換或快速傅里葉變換來完成，而從頻域到時(shí)域的轉(zhuǎn)換可以通過傅里葉逆變換或快速傅里葉逆變換來完成。

下圖展示了我們?nèi)绾问褂每焖俑道锶~變換代替卷積。

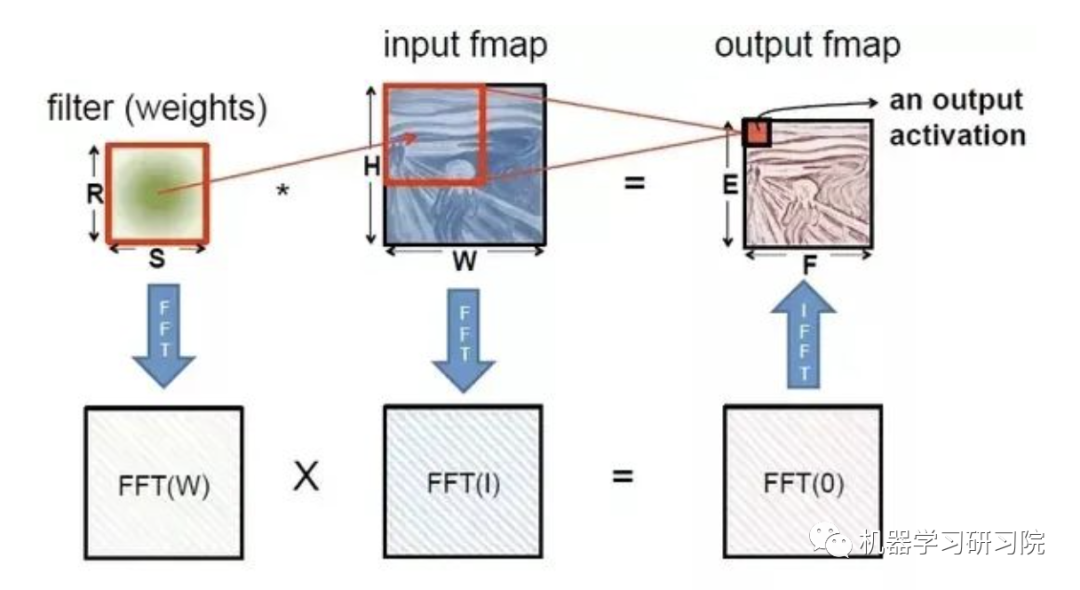
正如我們所討論的，在任何復(fù)雜的網(wǎng)絡(luò)中濾波器和層的數(shù)量都是非常高的，由于這些數(shù)量的增加，使用卷積的計(jì)算過程變得非常緩慢。而利用傅里葉變換可以減少這種計(jì)算的復(fù)雜性，使模型運(yùn)行速度更快。

如果你對(duì)這篇文章的思路有興趣可以自行嘗試，并歡迎討論。

責(zé)任編輯：彭菁