1
Motivation of Dual SVM
首先,我們回顧一下,對于非線性SVM,我們通常可以使用非線性變換將變量從x域轉換到z域中。然后,在z域中,根據上一節課的內容,使用線性SVM解決問題即可。上一節課我們說過,使用SVM得到large-margin,減少了有效的VC Dimension,限制了模型復雜度;另一方面,使用特征轉換,目的是讓模型更復雜,減小Ein。
所以說,非線性SVM是把這兩者目的結合起來,平衡這兩者的關系。那么,特征轉換下,求解QP問題在z域中的維度設為d^+1,如果模型越復雜,則d^+1越大,相應求解這個QP問題也變得很困難。當d^無限大的時候,問題將會變得難以求解,那么有沒有什么辦法可以解決這個問題呢?一種方法就是使SVM的求解過程不依賴d^,這就是我們本節課所要討論的主要內容。

比較一下,我們上一節課所講的Original SVM二次規劃問題的變量個數是d^+1,有N個限制條件;而本節課,我們把問題轉化為對偶問題(’Equivalent’ SVM),同樣是二次規劃,只不過變量個數變成N個,有N+1個限制條件。這種對偶SVM的好處就是問題只跟N有關,與d^無關,這樣就不存在上文提到的當d^無限大時難以求解的情況。

如何把問題轉化為對偶問題(’Equivalent’ SVM),其中的數學推導非常復雜,本文不做詳細數學論證,但是會從概念和原理上進行簡單的推導。

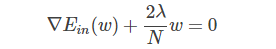
所以,在regularization問題中,λ是已知常量,求解過程變得容易。那么,對于dual SVM問題,同樣可以引入λ,將條件問題轉換為非條件問題,只不過λ是未知參數,且個數是N,需要對其進行求解。


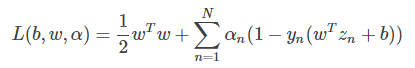
這個函數右邊第一項是SVM的目標,第二項是SVM的條件和拉格朗日因子αn的乘積。我們把這個函數稱為拉格朗日函數,其中包含三個參數:b,w,αn。

下面,我們利用拉格朗日函數,把SVM構造成一個非條件問題:


2
Lagrange Dual SVM
現在,我們已經將SVM問題轉化為與拉格朗日因子αn有關的最大最小值形式。已知αn≥0,那么對于任何固定的α′,且αn′≥0,一定有如下不等式成立:
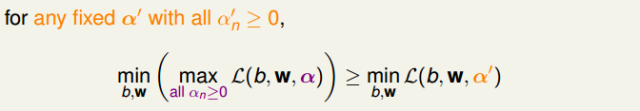
對上述不等式右邊取最大值,不等式同樣成立:

上述不等式表明,我們對SVM的min和max做了對調,滿足這樣的關系,這叫做Lagrange dual problem。不等式右邊是SVM問題的下界,我們接下來的目的就是求出這個下界。
已知≥是一種弱對偶關系,在二次規劃QP問題中,如果滿足以下三個條件:
- 函數是凸的(convex primal)
- 函數有解(feasible primal)
- 條件是線性的(linear constraints)
那么,上述不等式關系就變成強對偶關系,≥變成=,即一定存在滿足條件的解(b,w,α),使等式左邊和右邊都成立,SVM的解就轉化為右邊的形式。
經過推導,SVM對偶問題的解已經轉化為無條件形式:
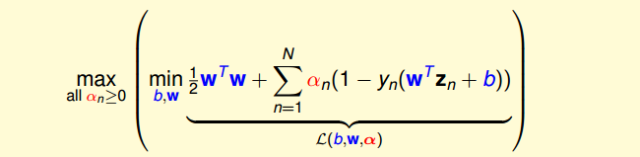
其中,上式括號里面的是對拉格朗日函數L(b,w,α)計算最小值。那么根據梯度下降算法思想:最小值位置滿足梯度為零。首先,令L(b,w,α)對參數b的梯度為零:
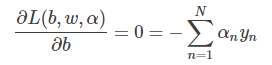

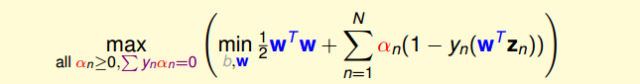
這樣,SVM表達式消去了b,問題化簡了一些。然后,再根據最小值思想,令L(b,w,α)對參數w的梯度為零:
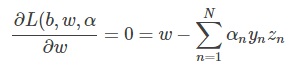
即得到:
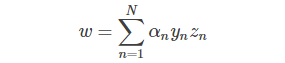

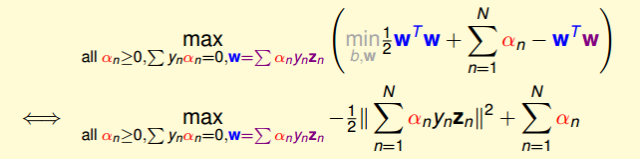
這樣,SVM表達式消去了w,問題更加簡化了。這時候的條件有3個:
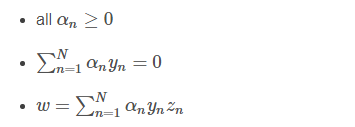

總結一下,SVM最佳化形式轉化為只與αn有關:
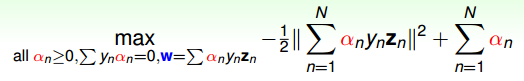
其中,滿足最佳化的條件稱之為Karush-Kuhn-Tucker(KKT):

在下一部分中,我們將利用KKT條件來計算最優化問題中的α,進而得到b和w。
3
Solving Dual SVM
上面我們已經得到了dual SVM的簡化版了,接下來,我們繼續對它進行一些優化。首先,將max問題轉化為min問題,再做一些條件整理和推導,得到:

顯然,這是一個convex的QP問題,且有N個變量αn,限制條件有N+1個。則根據上一節課講的QP解法,找到Q,p,A,c對應的值,用軟件工具包進行求解即可。






4
Messages behind Dual SVM
回憶一下,上一節課中,我們把位于分類線邊界上的點稱為support vector(candidates)。本節課前面介紹了αn>0的點一定落在分類線邊界上,這些點稱之為support vector(注意沒有candidates)。也就是說分類線上的點不一定都是支持向量,但是滿足αn>0的點,一定是支持向量。

SV只由αn>0的點決定,根據上一部分推導的w和b的計算公式,我們發現,w和b僅由SV即αn>0的點決定,簡化了計算量。這跟我們上一節課介紹的分類線只由“胖”邊界上的點所決定是一個道理。也就是說,樣本點可以分成兩類:一類是support vectors,通過support vectors可以求得fattest hyperplane;另一類不是support vectors,對我們求得fattest hyperplane沒有影響。

回過頭來,我們來比較一下SVM和PLA的w公式:


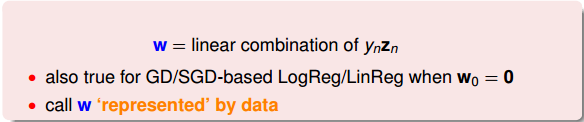
總結一下,本節課和上節課主要介紹了兩種形式的SVM,一種是Primal Hard-Margin SVM,另一種是Dual Hard_Margin SVM。Primal Hard-Margin SVM有d^+1個參數,有N個限制條件。當d^+1很大時,求解困難。而Dual Hard_Margin SVM有N個參數,有N+1個限制條件。當數據量N很大時,也同樣會增大計算難度。兩種形式都能得到w和b,求得fattest hyperplane。通常情況下,如果N不是很大,一般使用Dual SVM來解決問題。



5
Summary
本節課主要介紹了SVM的另一種形式:Dual SVM。我們這樣做的出發點是為了移除計算過程對d^的依賴。Dual SVM的推導過程是通過引入拉格朗日因子α,將SVM轉化為新的非條件形式。然后,利用QP,得到最佳解的拉格朗日因子α。再通過KKT條件,計算得到對應的w和b。最終求得fattest hyperplane。
-
Dual
+關注
關注
0文章
49瀏覽量
23250 -
向量機
+關注
關注
0文章
166瀏覽量
20929 -
SVM
+關注
關注
0文章
154瀏覽量
32543 -
kkt
+關注
關注
0文章
4瀏覽量
4015
發布評論請先 登錄
相關推薦
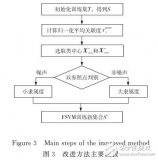
基于改進支持向量機的貨幣識別研究
基于支持向量機(SVM)的工業過程辨識
基于向量機隨機投影特征降維分類下降解決方案
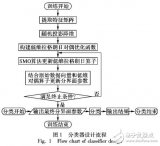
多分類孿生支持向量機研究進展
支持向量機的故障預測模型
什么是支持向量機 什么是支持向量
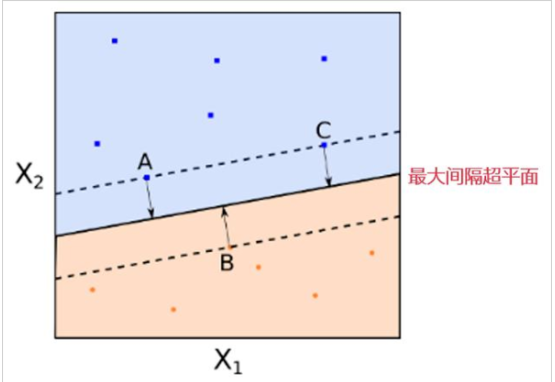




 對偶支持向量機DSVM
對偶支持向量機DSVM
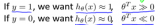
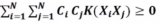











評論