優(yōu)化是機器學習中的關鍵步驟。在這個機器學習系列中，我們將簡要介紹優(yōu)化問題，然后探討兩種特定的優(yōu)化方法，即拉格朗日乘子和對偶分解。這兩種方法在機器學習、強化學習和圖模型中非常流行。

優(yōu)化問題

優(yōu)化問題通常定義為：

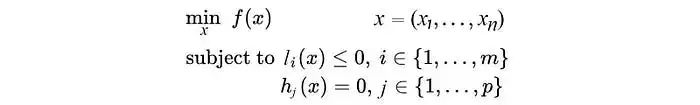
優(yōu)化問題包含一個目標函數(shù)和可選的不等式和等式約束。一般的優(yōu)化問題是NP難問題。但是，很多類別的凸優(yōu)化問題可以在多項式時間內解決。當我們將f(x?)和f(x?)相連形成下方的紅線時，如果f是一個凸函數(shù)，那么對于它們之間的點，紅線總是在f的上方，即 y? ≥ f(x?)。

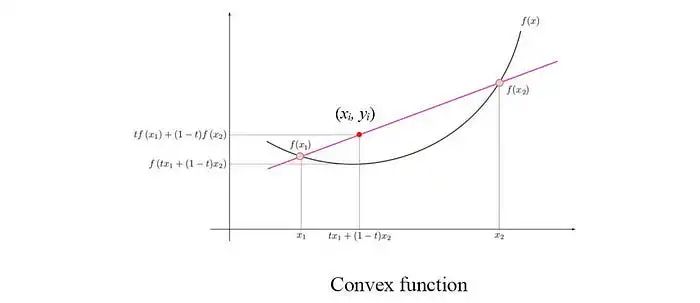
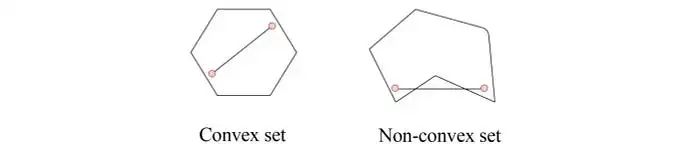
一個凸優(yōu)化問題具有凸目標函數(shù)和凸可行集的特征。可行集是滿足約束條件的x的集合。在凸集中，集合中兩個點之間的任何值也必須屬于凸集。

從另一個角度來看，在凸優(yōu)化問題中，f和l是凸函數(shù)，

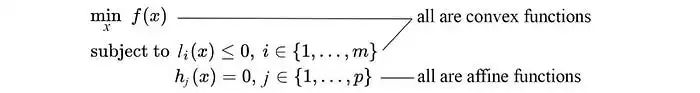
并且等式約束是仿射函數(shù)，其一般形式為：

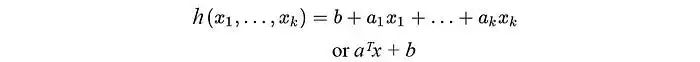
順帶一提，仿射函數(shù)是凸函數(shù)，這一點我們后面會用到。

在機器學習中，線性回歸的目標函數(shù)通常表示為最小二乘誤差。最小二乘優(yōu)化問題已經得到廣泛研究。有許多數(shù)值方法可以對它們進行求解，除非達到了某些可擴展性限制，否則它們可以通過解析方法（正規(guī)方程）解決。這在優(yōu)化問題中是相對容易解決的問題。

否則，如果機器學習問題可以表示為線性規(guī)劃問題，我們可以應用線性規(guī)劃。這也已經得到了廣泛的研究。線性規(guī)劃中x的可行集是一個多面體。

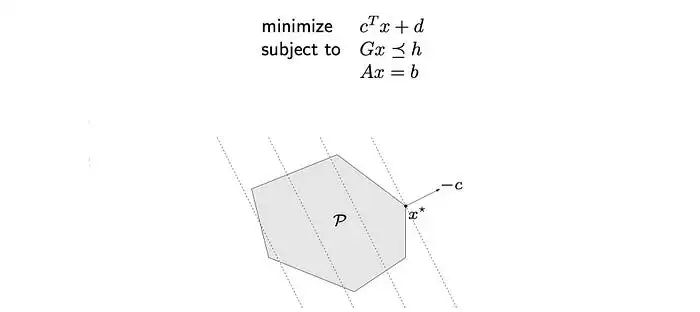
在我們上面的例子中，虛線是目標函數(shù)的等高線。最優(yōu)解x*將是其中一個頂點。

一般來說，如果問題是凸優(yōu)化問題，我們可以通過數(shù)值方法來解決。一個函數(shù)是凸函數(shù)，如果它的二階導數(shù)對于所有x都是正的。

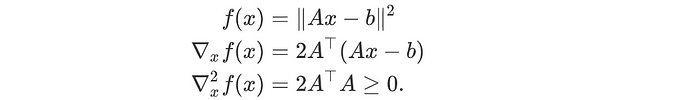
在機器學習中，我們經常將問題轉換、近似或放寬為這些更簡單的優(yōu)化模型之一。

拉格朗日乘子

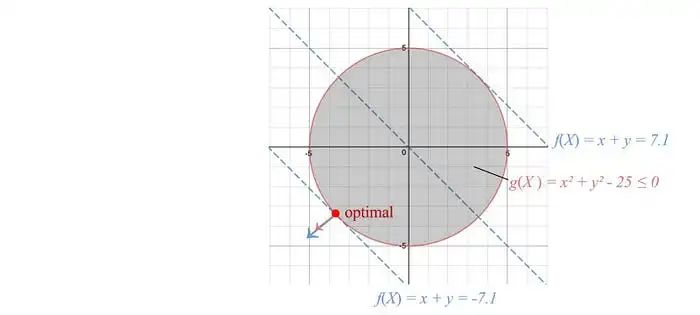
讓我們專注于尋找一個一般優(yōu)化問題的解。考慮代價函數(shù)為f=x+y，等式約束為h: x2 + y2 = 25，如下圖所示的紅色圓圈。

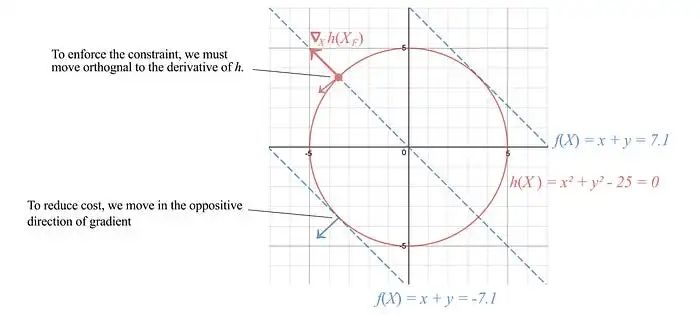
為了滿足約束條件，我們沿著約束面法線的正交方向移動，即垂直于?x h。為了降低代價，我們選擇沿著f的負梯度方向移動。當我們無法進一步移動以降低代價時，就達到了最優(yōu)點。這發(fā)生在?h與代價函數(shù)的梯度對齊時。

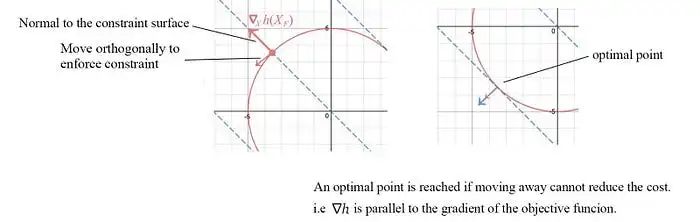
i.e.,

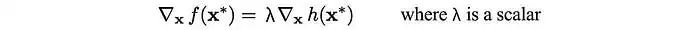
h(x) = 0也意味著-h(x) = 0。λ的符號取決于h的定義方式。因此，λ可以是正的、負的或零。

接下來，我們定義拉格朗日函數(shù)為：

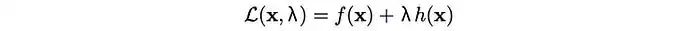
如果我們分別對拉格朗日函數(shù)關于x和λ求導，并將它們設置為零，如下所示，我們就可以強制執(zhí)行前面描述的最優(yōu)點以及等式約束。

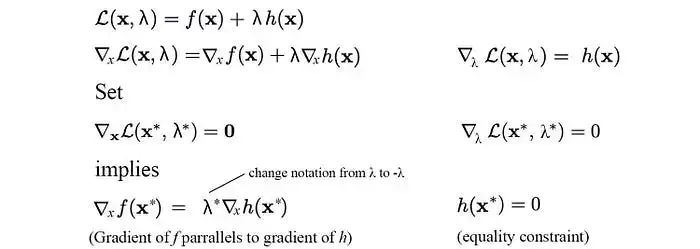
因此，通過找到關于x和λ的拉格朗日函數(shù)的最優(yōu)點，我們可以確定在強制執(zhí)行等式約束的情況下的最優(yōu)解。我們也可以在拉格朗日函數(shù)中有多個約束和不等式約束。優(yōu)化問題的形式將為：

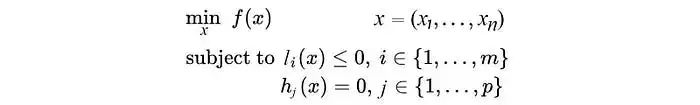
拉格朗日函數(shù)的定義如下:

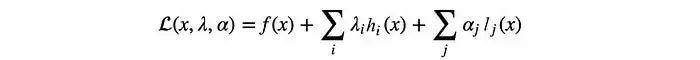
現(xiàn)在不等式約束要求最優(yōu)點在陰影區(qū)域內（包括邊界）。當解是最優(yōu)時，f和l的梯度將具有相同的方向，即α? ≥ 0。

讓我們再對不等式約束進行另一個觀察。下面的左圖表示一個具有最優(yōu)解為該圓圈中心的代價函數(shù)f。

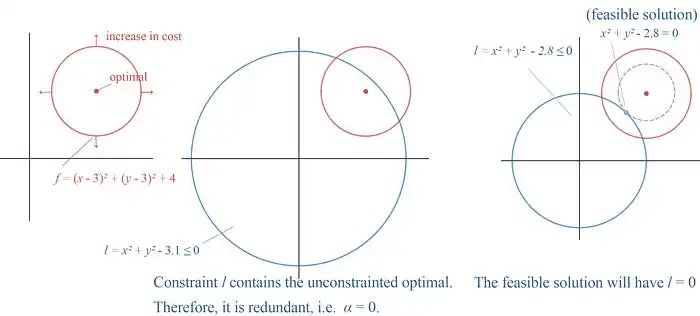
在中間的圖中，我們?yōu)閮?yōu)化問題添加了一個不等式約束。但是，這個約束是多余的，因為無約束最優(yōu)點已經滿足這個約束條件。因此，α?可以簡單地為零，表示它是多余的。

在右邊的圖中，無約束最優(yōu)解落在l的外面。我們必須增加代價（紅色圓圈）直到它與l相交。對應的最低代價將使得約束l等于0。

因此，α? l?(x) 總是等于0。

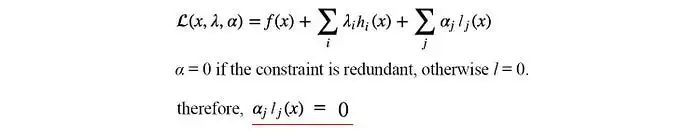
例子

讓我們最大化f(x, y) = x + y，滿足x2 + y2 = 32。

拉格朗日函數(shù)為：

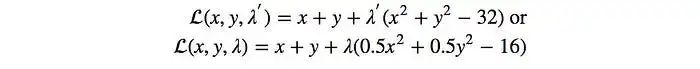
為了解決這個優(yōu)化問題，我們需要分別對