前言

在一次關于如何閱讀MTF曲線的網絡討論中，“光學規律太復雜而令人厭煩”，是一個公認的意見；可見，對于攝影師來說，理解數字的世界是那么的困難！

不過，情況并沒有那么糟糕，我將在接下來的內容向你展示，其實你并不需要掌握傅里葉高等光學之類的，也可以理解那些基本關系。讀完本文，你將能夠從制造商或測試機構發布的MTF數據中判斷鏡頭的特性。另外，我們還將介紹MTF的局限性，以便你可以批判地認識鏡頭評論。

一些人看到那么多公式曲線后，可能會說這些對于拍好照片并不是必需的，攝影更重要的是實踐；但以一個更好的方式理解你的工具，不挺有意義嗎？這也是我希望大家在閱讀本文后能得到的，下面我也會借助一些圖像向大家展示說明。

點擴散函數

當攝影師想拍一張逼真的圖片時，他們希望有一個理想的鏡頭，該鏡頭會將從物品某一點反射出的光線再匯聚于對應圖片上的一點。但實際的鏡頭只能達到部分的理想效果，而且現實中幾何意義的像點并不存在。鏡頭像差、制造公差以及光的波動性等則導致來自物方點光源的光線總是分布在理想的像點的周圍。

某種程度上，這片區域可能是最小的彌散圓：其中光線分布并不均勻，亮度從內到外逐漸減小，而且形狀也很少是圓形的。這種效應被稱為“點擴散函數”，其形狀和大小表征透鏡的圖像質量。

如果將攝影比作“繪畫”，則點擴散函數就是筆跡，即透鏡的“筆觸”，就像“筆跡”有寬、平、尖或硬的刷子，透鏡同樣有不同的類型的“筆跡”。

但是為什么不用它來定量描述圖像質量呢？有以下3點原因：

首先，點擴散函數的形狀有時非常復雜，不能使用簡單數字描述。如下圖所示，前六個擴散點圖是中等圖像質量的示例，也是全孔徑高速鏡頭、廣角鏡頭邊緣或輕微散焦的典型情況。

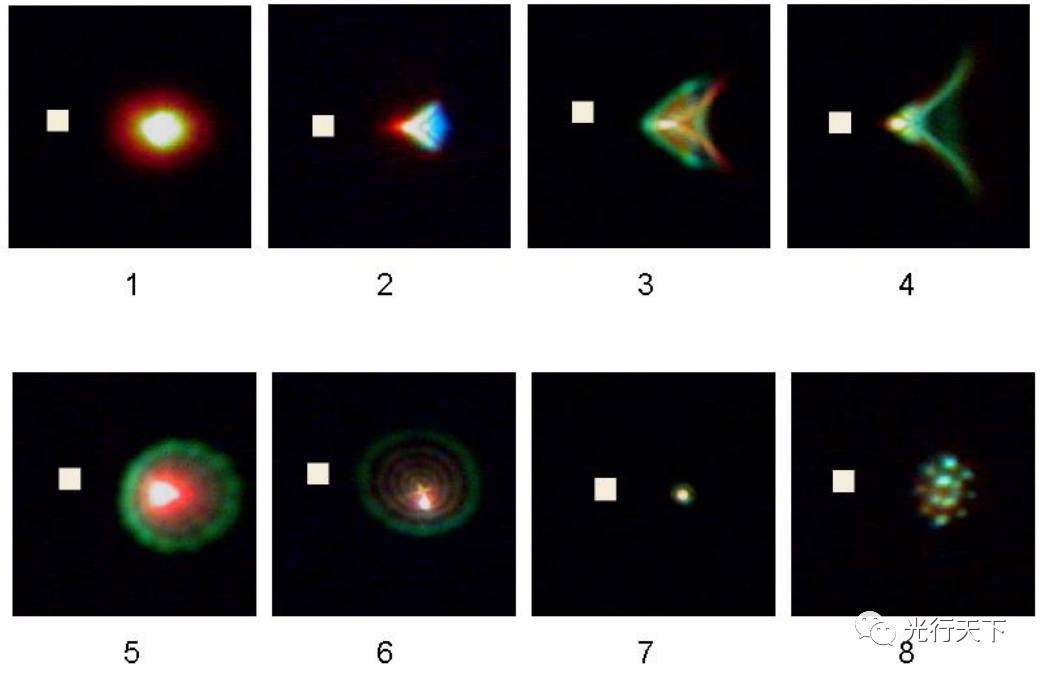
在1200萬像素、30mm全畫幅相機的以上每張圖片上都貼了一個8.5微米的白色方塊用于尺寸對比。所有這些擴散點都比這個方塊大得多。

圖7為優秀的圖像性能的擴散點圖，但在數字傳感器上通常看不到如此小的擴散點。最右邊的圖8為加載了低通濾波器后的擴散點，低通濾波器放在傳感器前用于抑制莫爾效應。而低通濾波器的幾個雙折射片放大了擴散點，導致圖像質量被人為降低。

第二個原因是幾乎沒有這種單一、孤立的擴散點。例如：只有在漆黑的夜晚拍攝星星時，才能達到與實驗室中相同的效果。絕大多數圖片在相機中以復雜的方式生成，是大量單個擴散點的疊加。

因為物體的某一小塊是由大量密集的點組成的，這些點對應于鏡頭后面圖像中的許多密集的理想像點。由于實際的擴散點不可能無限小，因此實際上擴散點會相互交疊，即圖像上一點的亮度是許多擴散點的二維積分。因此，筆觸和我們所看的圖像之間的數學關系并不是那么容易處理的。

第三個原因就是，我將要解釋的方法可以更完美的描述從鏡片到眼睛的整個圖像鏈。 調制傳遞

由于我們主要關注物體是如何成像的，物體不同于星星，它包含無窮多個點，因此我們必須找到另一種定量描述圖像質量的方法。我們使用正弦的亮度分布模型來研究一個盡可能簡單的物體是如何成像的。正弦亮度分布模型是明暗交替的條紋，其中明暗條紋的過渡是漸變且連續的（即正弦變化），就像我們插座中的電力隨時間的變化一樣。

我們選擇正弦變化的模型的原因是其圖像同樣是正弦函數變化的，無論其擴散點的形狀有多復雜。它的一些其他特性也保持穩定或至少與成像質量無關：條紋的方向不會改變，頻率（每單位長度的條紋數量）僅根據成像比例而變。

圖像的明暗條紋之間的亮度與原始模型的不再相同，主要因為擴散點的延伸（衍射），即部分光落在完全黑暗的區域而不是對應的明亮位置。

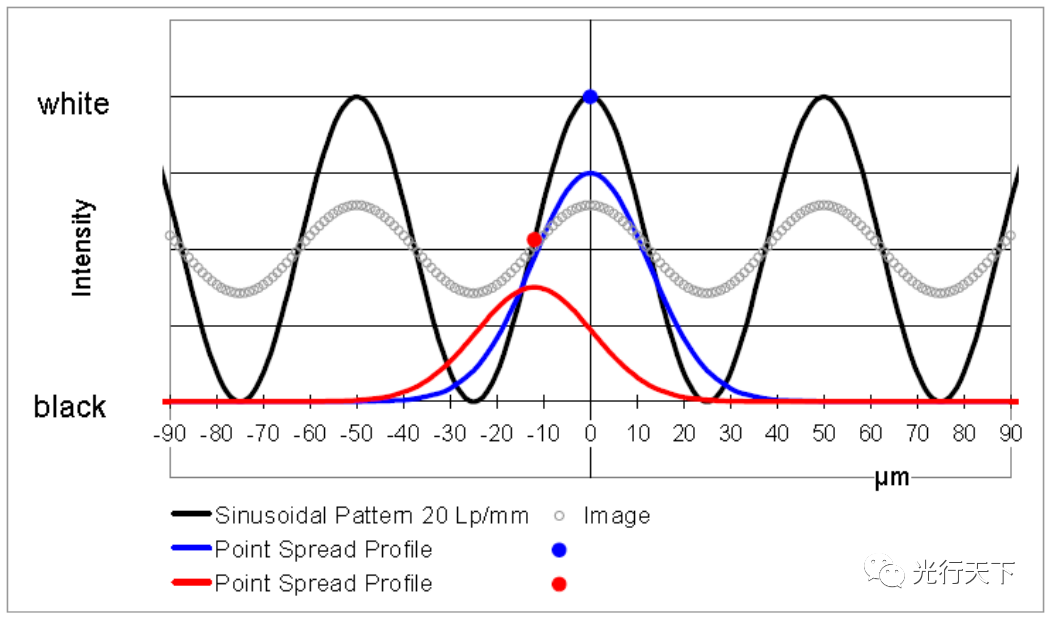上圖黑色曲線顯示了正弦條紋模型的強度分布（垂直于條紋的橫截面）；其每1mm有20個周期，每個周期50微米；紅色和藍色為擴散點的中心橫截面的亮度分布。藍色曲線即正弦模型上藍點的亮度在成像時分散到周圍區域的圖形，有一部分光落入藍點旁邊25微米的“黑暗山谷”。