傅里葉變換的公式為：

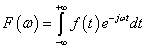
可以把傅里葉變換也成另外一種形式：

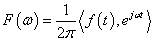
可以看出，傅里葉變換的本質是內積，三角函數是完備的正交函數集，不同頻率的三角函數的之間的內積為0，只有頻率相等的三角函數做內積時，才不為0。

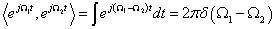
下面從公式解釋下傅里葉變換的意義

因為傅里葉變換的本質是內積，所以f(t)和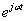求內積的時候，只有f(t)中頻率為ω的分量才會有內積的結果，其余分量的內積為0。可以理解為f(t)在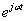上的投影，積分值是時間從負無窮到正無窮的積分，就是把信號每個時間在ω的分量疊加起來，可以理解為f(t)在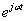上的投影的疊加，疊加的結果就是頻率為ω的分量，也就形成了頻譜。

傅里葉逆變換的公式為：

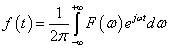
下面從公式分析下傅里葉逆變換的意義

傅里葉逆變換就是傅里葉變換的逆過程，在F(ω)和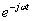求內積的時候，F(ω)只有t時刻的分量內積才會有結果，其余時間分量內積結果為0，同樣積分值是頻率從負無窮到正無窮的積分，就是把信號在每個頻率在t時刻上的分量疊加起來，疊加的結果就是f(t)在t時刻的值，這就回到了我們觀察信號最初的時域。

對一個信號做傅里葉變換，然后直接做逆變換，這樣做是沒有意義的，在傅里葉變換和傅里葉逆變換之間有一個濾波的過程。將不要的頻率分量給濾除掉，然后再做逆變換，就得到了想要的信號。比如信號中摻雜著噪聲信號，可以通過濾波器將噪聲信號的頻率給去除，再做傅里葉逆變換，就得到了沒有噪聲的信號。

優點：頻率的定位很好，通過對信號的頻率分辨率很好，可以清晰的得到信號所包含的頻率成分，也就是頻譜。

缺點：因為頻譜是時間從負無窮到正無窮的疊加，所以，知道某一頻率，不能判斷，該頻率的時間定位。不能判斷某一時間段的頻率成分。

例子：

平穩信號：

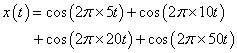
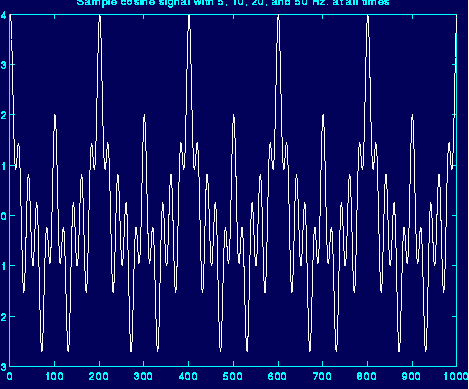
傅里葉變換的結果：

由于信號是平穩信號，每處的頻率都相等，所以看不到傅里葉變換的缺點。

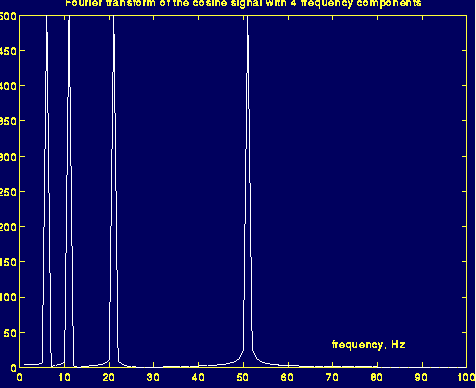
對于非平穩信號：信號是余弦信號，仍然有四個頻率分量

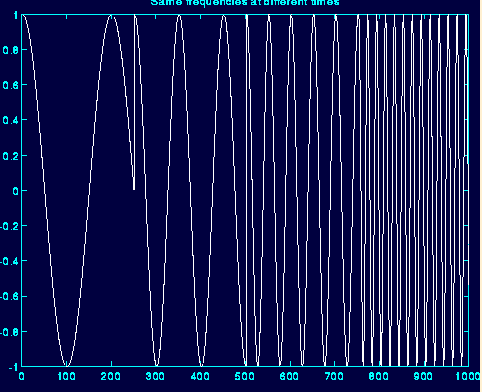
傅里葉變換的結果：

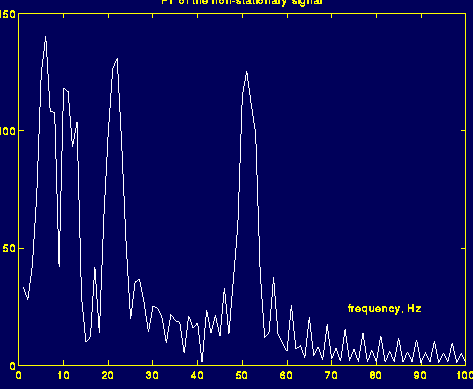
由上圖看出知道某一頻率，不能判斷，該頻率的時間定位。不能判斷某一時間段的頻率成分。

短時傅里葉變換

傅里葉變換存在著嚴重的缺點，就是不能實現時頻聯合分析。傅里葉變換要從負無窮計算到正無窮，這在實際使用當中，跟即時性分析會有很大的矛盾。根據這一缺點，提出了短時傅里葉變換。后來的時間—頻率分析也是以短時傅里葉變換為基礎提出的。

為了彌補傅里葉變換的缺陷，給信號加上一個窗函數，對信號加窗后計算加窗后函數的傅里葉變換，加窗后得到時間附近的很小時間上的局部譜，窗函數可以根據時間的位置變化在整個時間軸上平移，利用窗函數可以得到任意位置附近的時間段頻譜，實現了時間局域化。

短時傅里葉變換的公式為：

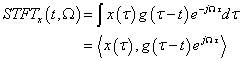
在時域用窗函數去截信號，對截下來的局部信號作傅立葉變換，即在t時刻得該段信號得傅立葉變換，不斷地移動t，也即不斷地移動窗函數的中心位置，即可得到不同時刻的傅立葉變換，這樣就得到了時間—頻率分析。

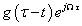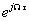短時傅里葉變換的本質和傅里葉變換一樣都是內積，只不過用代替了，實現了局部信號的頻譜分析。

短時傅里葉變換的另一種形式：

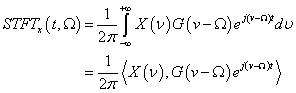
該式子表明在時域里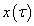加窗函數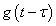，得出在頻域里對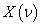加窗。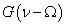

優點：在傅里葉變換的基礎上，增加了窗函數，就實現了時間—頻率分析。

缺點：短時傅里葉變換使用一個固定的窗函數，窗函數一旦確定了以后，其形狀就不再發生改變，短時傅里葉變換的分辨率也就確定了。如果要改變分辨率，則需要重新選擇窗函數。短時傅里葉變換用來分析分段平穩信號或者近似平穩信號猶可，但是對于非平穩信號，當信號變化劇烈時，要求窗函數有較高的時間分辨率；而波形變化比較平緩的時刻，主要是低頻信號，則要求窗函數有較高的頻率分辨率。短時傅里葉變換不能兼顧頻率與時間分辨率的需求。測不準原理告訴我們，不可能在時間和頻率兩個空間同時以任意精度逼近被測信號，因此就必須在信號的分析上對時間或者頻率的精度做取舍。短時傅里葉變換受到測不準原理的限制，所以短時傅里葉變換窗函數的時間與頻率分辨率不能同時達到最優。在實際使用時，根據實際情況選用合適的窗函數。

例子：

原始信號：信號是余弦信號，有四個頻率分量.

當窗函數選為：

短時傅里葉變換為：

由上圖可以看出，時域的分辨率比較好，但是頻率出現一定寬度的帶寬，也就是說頻率分辨率差；

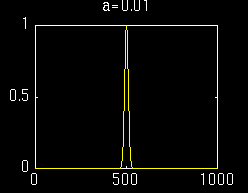
當窗函數選擇為：

短時傅里葉變換為：

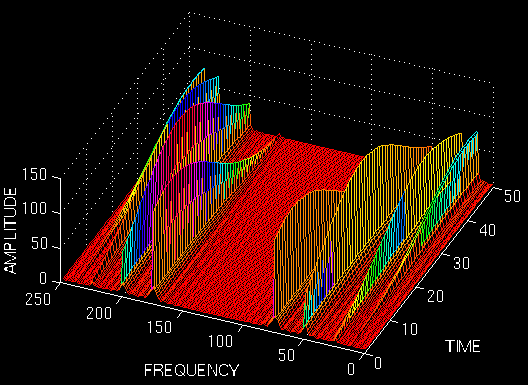
由上圖可以看出，頻率的分辨率比較好，但是時域分辨率差，有點接近傅里葉變換。由上圖可以看到短時傅里葉變換的缺點。

來源：道客巴巴《傅里葉變換本質及其公式解析》，由cuyongo69615分享

審核編輯：湯梓紅