溫馨提示:全文14632字,因?yàn)槲恼麻L(zhǎng)度問題 需要分五篇讀完 詳細(xì)文章可以進(jìn)我主頁!
今天就把常見****查找算法也總結(jié)個(gè)通透, 還有詳細(xì)的代碼解釋, 真的是寫完這篇感覺腦子已經(jīng)不是自己的了,還希望大家好好利用。
查找算法,顧名思義就是在一堆數(shù)據(jù)中查找到你想要的那個(gè)數(shù)據(jù)。 以下就介紹幾種常用的查找算法,幫助大家更好的了解其原理和使用場(chǎng)景。

1、線性查找
1.1、基本概念及適用場(chǎng)景
線性查找(Linear Search),也叫順序查找,是一種簡(jiǎn)單的查找算法,適用于無序數(shù)組或鏈表中的元素查找。線性查找的原理是按順序依次掃描待查找的元素,直到找到目標(biāo)元素或掃描完所有元素。
具體實(shí)現(xiàn)時(shí),從數(shù)組的第一個(gè)元素開始逐個(gè)比較,如果找到目標(biāo)元素,則返回其下標(biāo),否則返回未找到的標(biāo)記(如-1)。如果數(shù)組中存在多個(gè)目標(biāo)元素,則只會(huì)找到第一個(gè)。
線性查找的時(shí)間復(fù)雜度為O(n),其中n是待查找元素的個(gè)數(shù),最壞情況下需要掃描整個(gè)數(shù)組或鏈表。
線性查找適用于以下情況:
- 待查找的數(shù)據(jù)規(guī)模較小,或數(shù)據(jù)無序,或需要查詢的數(shù)據(jù)在數(shù)組或鏈表的末尾。
- 數(shù)據(jù)存儲(chǔ)在單向鏈表中,沒有下標(biāo)的概念。
需要注意的是,線性查找的效率比較低,不適用于大規(guī)模的數(shù)據(jù)查詢。
1.2、代碼示例
#include
int linearSearch(int arr[], int n, int x) {
int i;
for (i = 0; i < n; i++) {
if (arr[i] == x) {
return i; // 找到了,返回元素下標(biāo)
}
}
return -1; // 沒找到,返回-1
}
int main() {
int arr[] = {10, 20, 30, 40, 50, 60};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 40;
int result = linearSearch(arr, n, x);
if (result == -1) {
printf("元素 %d 不存在\\n", x);
} else {
printf("元素 %d 的下標(biāo)是 %d\\n", x, result);
}
return 0;
}
在上述示例中,linearSearch()函數(shù)用于進(jìn)行線性查找,參數(shù) arr 表示要查找的數(shù)組,n 表示數(shù)組的長(zhǎng)度,x 表示要查找的元素值。函數(shù)通過遍歷數(shù)組中的每個(gè)元素,找到目標(biāo)元素就返回其下標(biāo),若未找到則返回 -1。在 main() 函數(shù)中,聲明數(shù)組并調(diào)用 linearSearch() 函數(shù)進(jìn)行查找,最終輸出查找結(jié)果。
2、二分查找
2.1、基本原理及注意事項(xiàng)
二分查找(Binary Search),也稱折半查找,是一種常見的查找算法。它的 基本原理是在有序數(shù)組中查找目標(biāo)元素,通過將目標(biāo)元素與有序數(shù)組的中間元素進(jìn)行比較,可以排除一半的元素,從而提高查找效率 。
二分查找適用于有序數(shù)組中的查找,可以用于查找具有單調(diào)性質(zhì)的數(shù)據(jù)集合。其時(shí)間復(fù)雜度為 O(log n),相對(duì)于線性查找的 O(n),效率更高。但是,二分查找的前提是必須有序,如果需要頻繁的插入和刪除操作,那么維護(hù)有序性就需要額外的操作,會(huì)降低效率。
在使用二分查找時(shí)需要注意以下幾點(diǎn):
- 數(shù)組必須有序。
- 二分查找只適用于靜態(tài)查找,即目標(biāo)數(shù)組不經(jīng)常變化。
- 目標(biāo)元素必須是可比較的,可以使用小于或大于操作符進(jìn)行比較。
- 二分查找的效率高于線性查找,但在小數(shù)據(jù)量的查找中,可能沒有線性查找快。
二分查找的應(yīng)用場(chǎng)景包括查找有序數(shù)組中的特定元素、查找第一個(gè)大于或小于給定值的元素等。
需要注意的是,雖然二分查找是一種高效的查找算法,但是在實(shí)際開發(fā)中,有時(shí)候使用哈希表等其他數(shù)據(jù)結(jié)構(gòu)也能達(dá)到更高的效率,所以需要根據(jù)具體的問題場(chǎng)景選擇合適的算法。
2.2、代碼示例
當(dāng)在一個(gè)有序數(shù)組查找某個(gè)元素時(shí),二分查找是一個(gè)很高效的算法。
#include
int binarySearch(int arr[], int l, int r, int x) {
if (r >= l) {
int mid = l + (r - l) / 2;
if (arr[mid] == x) {
return mid;
}
if (arr[mid] > x) {
return binarySearch(arr, l, mid - 1, x);
}
return binarySearch(arr, mid + 1, r, x);
}
return -1;
}
int main() {
int arr[] = {1, 3, 5, 7, 9, 11, 13};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 7;
int result = binarySearch(arr, 0, n - 1, x);
if (result == -1) {
printf("元素不在數(shù)組中");
} else {
printf("元素在數(shù)組中的索引為:%d", result);
}
return 0;
}
該代碼實(shí)現(xiàn)了一個(gè)名為binarySearch的函數(shù),該函數(shù)用于在一個(gè)有序數(shù)組中查找給定的元素。binarySearch函數(shù)的參數(shù)為待查找數(shù)組arr,數(shù)組左邊界l,數(shù)組右邊界r以及要查找的元素x。
在函數(shù)內(nèi)部,首先通過計(jì)算中間元素的下標(biāo)來將待查找區(qū)間分為兩部分。如果中間元素等于要查找的元素,則直接返回中間元素的下標(biāo)。如果中間元素大于要查找的元素,則在左半部分進(jìn)行遞歸查找。否則,在右半部分進(jìn)行遞歸查找。
在main函數(shù)中,先定義了一個(gè)有序數(shù)組arr,以及要查找的元素x。然后,調(diào)用binarySearch函數(shù)查找給定元素,并將返回值保存在變量result中。如果result的值為-1,則說明要查找的元素不在數(shù)組中;否則,輸出要查找的元素在數(shù)組中的索引。
需要注意的是,二分查找算法要求待查找的數(shù)組必須是有序的。因此,在使用二分查找算法前,需要保證待查找的數(shù)組已經(jīng)排好序。
3、插值查找
3.1、基本概念
插值查找是一種基于二分查找算法的優(yōu)化,它的基本原理與二分查找類似,只不過插值查找根據(jù)查找鍵值與查找范圍內(nèi)值的分布情況,通過插值來確定下一步查找的位置。與二分查找相比,它可以提供更快的查找速度,尤其是數(shù)據(jù)比較分散的情況下,比如數(shù)據(jù)集中在數(shù)組的前面或后面。
插值查找的具體實(shí)現(xiàn)步驟如下:
- 確定查找范圍,初始化起始位置left為0,結(jié)束位置right為n-1,其中n為數(shù)組長(zhǎng)度。
- 計(jì)算中間位置mid,mid的值為 (key - arr[left]) / (arr[right] - arr[left]) * (right - left) + left,其中key為查找關(guān)鍵字,arr為待查找的有序數(shù)組。
- 如果arr[mid]等于key,則返回mid。
- 如果arr[mid]小于key,則在[mid+1, right]范圍內(nèi)查找。
- 如果arr[mid]大于key,則在[left, mid-1]范圍內(nèi)查找。
- 重復(fù)2-5步,直到查找到目標(biāo)值或查找范圍為空,查找失敗。
需要注意的是,插值查找要求待查找的數(shù)組是有序的,否則無法保證查找結(jié)果的正確性。 此外,當(dāng)數(shù)據(jù)分布較為均勻時(shí),插值查找可以快速定位到目標(biāo)值,但當(dāng)數(shù)據(jù)分布不均時(shí),可能會(huì)導(dǎo)致查找效率的降低。
3.2、代碼示例
#include
// 插值查找函數(shù),array為待查找數(shù)組,n為數(shù)組長(zhǎng)度,target為目標(biāo)值
int interpolationSearch(int array[], int n, int target) {
int low = 0, high = n - 1;
while (low <= high && target >= array[low] && target <= array[high]) {
int pos = low + ((double)(target - array[low]) / (array[high] - array[low])) * (high - low);
if (array[pos] == target) {
return pos;
} else if (array[pos] < target) {
low = pos + 1;
} else {
high = pos - 1;
}
}
return -1;
}
// 測(cè)試
int main() {
int array[] = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 };
int n = sizeof(array) / sizeof(int);
int target = 12;
int index = interpolationSearch(array, n, target);
if (index != -1) {
printf("目標(biāo)值%d在數(shù)組中的位置是%d\\n", target, index);
} else {
printf("目標(biāo)值%d在數(shù)組中不存在\\n", target);
}
return 0;
}
在上面的代碼中,interpolationSearch() 函數(shù)采用了插值查找算法的實(shí)現(xiàn),其中 array 為待查找數(shù)組,n 表示數(shù)組長(zhǎng)度,target 表示目標(biāo)值。在查找過程中,我們首先計(jì)算出目標(biāo)值所在的估計(jì)位置 pos,然后根據(jù) array[pos] 的值與目標(biāo)值 target 的大小進(jìn)行比較,并更新查找的范圍,直到找到目標(biāo)值或者確定目標(biāo)值不存在于數(shù)組中。最終,該函數(shù)返回目標(biāo)值在數(shù)組中的位置,如果不存在則返回 -1。
在 main() 函數(shù)中,我們定義了一個(gè)數(shù)組 array 和目標(biāo)值 target,并調(diào)用 interpolationSearch() 函數(shù)進(jìn)行查找,將結(jié)果輸出到控制臺(tái)。
-
數(shù)據(jù)
+關(guān)注
關(guān)注
8文章
7145瀏覽量
89585 -
代碼
+關(guān)注
關(guān)注
30文章
4828瀏覽量
69058 -
查找算法
+關(guān)注
關(guān)注
0文章
6瀏覽量
5540
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
STM32 library、應(yīng)用、源代碼等資料 歸檔貼(查找方便)
簡(jiǎn)單的查找算法
isis 7 professional_元件查找代碼
圖論算法及MATLAB程序代碼的詳細(xì)資料說明
詳解C語言二分查找算法細(xì)節(jié)
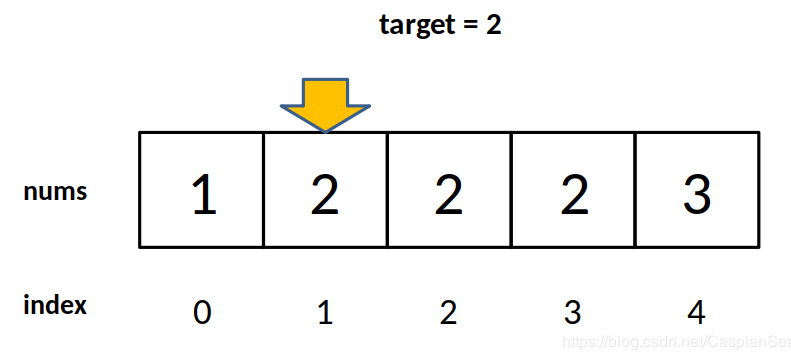




 常見的查找算法匯總(含詳細(xì)代碼)1
常見的查找算法匯總(含詳細(xì)代碼)1












評(píng)論