沒事兒的時候我喜歡玩玩那些經(jīng)典的 2D 網(wǎng)頁小游戲，我發(fā)現(xiàn)很多游戲都要涉及地圖的隨機生成，比如掃雷游戲中地雷的位置應(yīng)該是隨機分布的：

再比如經(jīng)典炸彈人游戲，障礙物的位置也是有一定隨機性的：

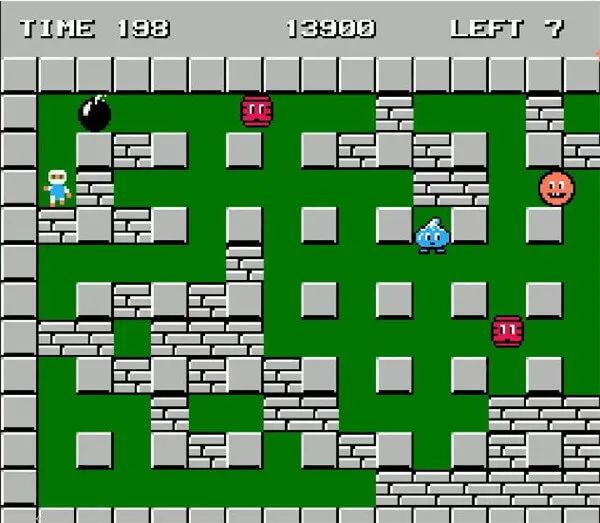
這些 2D 游戲相較現(xiàn)在的大型 3D 游戲雖然看起來有些簡陋，但依然用到很多有趣算法技巧，本文就來深入研究一下地圖的隨機生成算法。

2D 游戲的地圖肯定可以抽象成一個二維矩陣，就拿掃雷舉例吧，我們可以用下面這個類表示掃雷的棋盤：

class Game {
    int m, n;
    // 大小為 m * n 的二維棋盤
    // 值為 true 的地方代表有雷，false 代表沒有雷
    boolean[][] board;
}

如果你想在棋盤中隨機生成k個地雷，也就是說你需要在board中生成k個不同的(x, y)坐標(biāo)，且這里面x, y都是隨機生成的。

對于這個需求， 首先一個優(yōu)化就是對二維矩陣進(jìn)行「降維打擊」，把二維數(shù)組轉(zhuǎn)化成一維數(shù)組 ：

class Game {
    int m, n;
    // 長度為 m * n 的一維棋盤
    // 值為 true 的地方代表有雷，false 代表沒有雷
    boolean[] board;

    // 將二維數(shù)組中的坐標(biāo) (x, y) 轉(zhuǎn)化為一維數(shù)組中的索引
    int encode(int x, int y) {
        return x * n + y;
    }

    // 將一維數(shù)組中的索引轉(zhuǎn)化為二維數(shù)組中的坐標(biāo) (x, y)
    int[] decode(int index) {
        return new int[] {index / n, index % n};
    }
}

這樣，我們只要在[0, m * n)中選取一個隨機數(shù)，就相當(dāng)于在二維數(shù)組中隨機選取了一個元素。

但問題是，我們現(xiàn)在需要隨機選出k個不同的位置放地雷。你可能說，那在[0, m * n)中選出來k個隨機數(shù)不就行了？

是的，但實際操作起來有些麻煩，因為你很難保證隨機數(shù)不重復(fù)。如果出現(xiàn)重復(fù)的隨機數(shù)，你就得再隨機選一次，直到找到k個不同的隨機數(shù)。

如果k比較小m * n比較大，那出現(xiàn)重復(fù)隨機數(shù)的概率還比較低，但如果k和m * n的大小接近，那么出現(xiàn)重復(fù)隨機數(shù)的概率非常高，算法的效率就會大幅下降。

那么，我們有沒有更好的辦法能夠在線性的時間復(fù)雜度解決這個問題？其實是有的，而且有很多種解決方案。

洗牌算法

第一個解決方案，我們可以換個思路，避開「在數(shù)組中隨機選擇k個元素」這個問題，把問題轉(zhuǎn)化成「如何隨機打亂一個數(shù)組」 。

現(xiàn)在想隨機初始化k顆地雷的位置，你可以先把這k顆地雷放在board開頭，然后把board數(shù)組隨機打亂，這樣地雷不就隨機分布到board數(shù)組的各個地方了嗎？

洗牌算法，或者叫隨機亂置算法就是專門解決這個問題的，我們可以看下力扣第 384 題「打亂數(shù)組」：

這個shuffle函數(shù)是算法的關(guān)鍵，直接看解法代碼吧：

class Solution {
    private int[] nums;
    private Random rand = new Random();
    
    public Solution(int[] nums) {
        this.nums = nums;
    }
    
    public int[] reset() {
        return nums;
    }
    
    // 洗牌算法
    public int[] shuffle() {
        int n = nums.length;
        int[] copy =  Arrays.copyOf(nums, n);
        for (int i = 0 ; i < n; i++) {
            // 生成一個 [i, n-1] 區(qū)間內(nèi)的隨機數(shù)
            int r = i + rand.nextInt(n - i);
            // 交換 nums[i] 和 nums[r]
            swap(copy, i, r);
        }
        return copy;
    }
    
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

洗牌算法的時間復(fù)雜度是 O(N)，而且邏輯很簡單，關(guān)鍵在于讓你證明為什么這樣做是正確的。排序算法的結(jié)果是唯一可以很容易檢驗的，但隨機亂置算法不一樣，亂可以有很多種，你怎么能證明你的算法是「真的亂」呢？

分析洗牌算法正確性的準(zhǔn)則：產(chǎn)生的結(jié)果必須有n!種可能 。這個很好解釋，因為一個長度為n的數(shù)組的全排列就有n!種，也就是說打亂結(jié)果總共有n!種。算法必須能夠反映這個事實，才是正確的。

有了這個原則再看代碼應(yīng)該就容易理解了：

對于nums[0]，我們把它隨機換到了索引[0, n)上，共有n種可能性；

對于nums[1]，我們把它隨機換到了索引[1, n)上，共有n - 1種可能性；

對于nums[2]，我們把它隨機換到了索引[2, n)上，共有n - 2種可能性；

以此類推，該算法可以生成n!種可能的結(jié)果，所以這個算法是正確的，能夠保證隨機性。

水塘抽樣算法

學(xué)會了洗牌算法，掃雷游戲的地雷隨機初始化問題就解決了。不過別忘了，洗牌算法只是一個取巧方案，我們還是得面對「在若干元素中隨機選擇k個元素」這個終極問題。

要知道洗牌算法能夠生效的前提是你使用數(shù)組這種數(shù)據(jù)結(jié)構(gòu)，如果讓你在一條鏈表中隨機選擇k個元素，肯定不能再用洗牌算法來蒙混過關(guān)了。

再比如，假設(shè)我們的掃雷游戲中棋盤的長和寬非常大，已經(jīng)不能在內(nèi)存中裝下一個大小為m * n的board數(shù)組了，我們只能維護(hù)一個大小為k的數(shù)組記錄地雷的位置：

class Game {
    // 棋盤的行數(shù)和列數(shù)（非常大）
    int m, n;
    // 長度為 k 的數(shù)組，記錄 k 個地雷的一維索引
    int[] mines;

    // 將二維數(shù)組中的坐標(biāo) (x, y) 轉(zhuǎn)化為一維數(shù)組中的索引
    int encode(int x, int y) {
        return x * n + y;
    }

    // 將一維數(shù)組中的索引轉(zhuǎn)化為二維數(shù)組中的坐標(biāo) (x, y)
    int[] decode(int index) {
        return new int[] {index / n, index % n};
    }
}

這樣的話，我們必須想辦法在[0, m*n)中隨機選取k個不同的數(shù)字了。

這就是常見的隨機抽樣場景，常用的解法是水塘抽樣算法（Reservoir Sampling） 。水塘抽樣算法是一種隨機概率算法，會者不難，難者不會。

我第一次見到這個算法問題是谷歌的一道算法題：給你一個未知長度的單鏈表，請你設(shè)計一個算法， 只能遍歷一次 ，隨機地返回鏈表中的一個節(jié)點。

這里說的隨機是均勻隨機（uniform random），也就是說，如果有n個元素，每個元素被選中的概率都是1/n，不可以有統(tǒng)計意義上的偏差。

一般的想法就是，我先遍歷一遍鏈表，得到鏈表的總長度n，再生成一個[0,n-1)之間的隨機數(shù)為索引，然后找到索引對應(yīng)的節(jié)點。但這不符合只能遍歷一次鏈表的要求。

這個問題的難點在于隨機選擇是「動態(tài)」的，比如說你現(xiàn)在你已經(jīng)遍歷了 5 個元素，你已經(jīng)隨機選取了其中的某個元素a作為結(jié)果，但是現(xiàn)在再給你一個新元素b，你應(yīng)該留著a還是將b作為結(jié)果呢？以什么邏輯做出的選擇，才能保證你的選擇方法在概率上是公平的呢？