1、線性方程組的求解

（1）矩陣的初等行變換：矩陣的初等行變換有三種變換，即交換兩行，以數k乘某行所有元素，將某一行的k倍加到另一行。例如將如下矩陣進行行變換有：

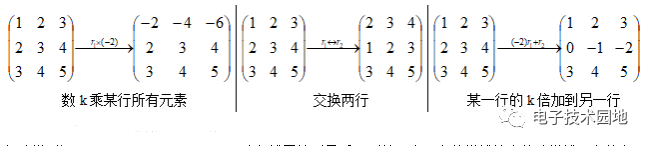
（2）行階梯型矩陣與行最簡形矩陣

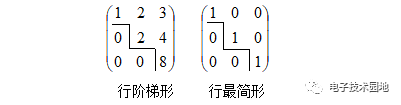
行階梯型矩陣是：從第一行某元素左方的豎線開始到最后一列某元素下方的橫線結束的階梯線，它的左下方的元素全為0；每段豎線的高度為一行，豎線的右方的第一個元素非零，如圖所示：

行最簡形矩陣是：若行階梯型矩陣非零行的首個非零元素為1，且非零元素所在的列其他元素均為0，如圖所示：

（3）求解齊次線性方程組的步驟是：將方程組的系數寫成矩陣形式，然后采用初等行變換將矩陣化為行階梯型矩陣或行最簡形矩陣。

（4）方程組的解具有三種可能：有唯一解，有無窮多解和無解。

齊次線性方程組不可能無解，最次也有0解，故齊次線性方程組只有兩種情況：若系數矩陣存在全0行，則方程組有無窮多解，若不存在全0行，則方程組有唯一解。

非齊次線性方程組由于增加了一列方程中等號后面的元素，所以有三種情況，若系數矩陣存在全0行，則方程組有無窮多解，若系數全為0且等號后面的數也為0，則方程組有唯一解，若系數全為0但等號后面的數不為0，則方程組無解。

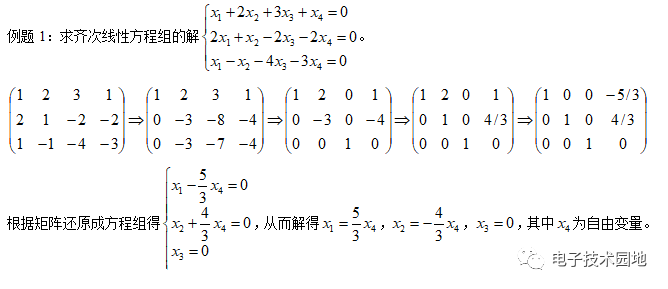
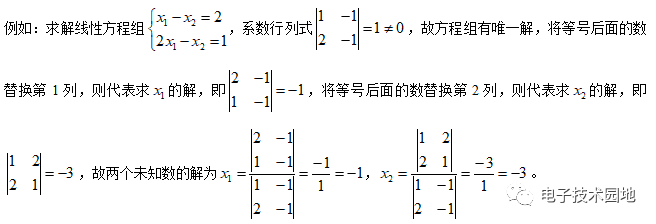
（5）克拉默法則：建議克拉默法則最好只用在有2個未知數的方程組。

寫出系數行列式，若系數行列式不為0，則方程組有唯一解，反之，放棄克拉默法則。

2、多項式合并為乘積的形式

（1）二次多項式的合并：對于二次多項式，一般可以湊完全平方公式或者采用因式分解的方式變為乘積的形式，如

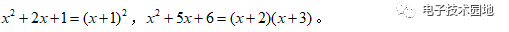
（2）三階以上多項式的合并

方法1：采用楊輝三角可以根據系數看出乘積的形式，楊輝三角的排列如下圖所示：

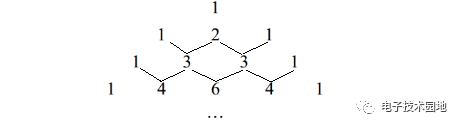
方法2：多項式除法，無論是階次多高的方程，只要能看出一個使等式為0的解，即可采用多項式除法。

方法3：利用恒等的原則，將奇次項與偶此項劃分在等式兩邊進行合并同類項。

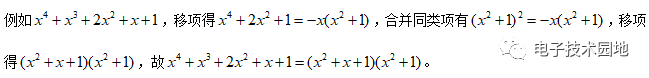
3、 乘積形式化為代數和形式 （有理函數拆分）

對于有理函數的拆分，首先將分母寫為乘積的形式，而后采用如下兩種方法之一即可。分母寫為乘積形式有兩種情況需要注意：

4、此外，函數的求導，積分，級數求和在電路分析中也經常用到，這三部分內容請參照高等數學學習即可。