1.1.6 模糊推理的運用

1.2.7 模糊控制系統的組成

與一般的計算機控制系統不同的是,模糊控制系統的控制器是模糊控制器,模糊控制器是基于模糊條件語句描述的語言控制規則,又稱為模糊語言控制器。
輸入輸出變量
(1)模糊控制的輸入變量通常取E或E,EC或E,EC,ER,分別構成所謂的一維,二維,三維模糊控制器,一般選擇控制量的增量作為模糊控制器的輸出變量。
(2)描述模糊控制器的輸入,輸出變量狀態:負大(NB),負中(NM),負小(NS),零(O),正小(PS),正中(PM),正大(PB)。
(3)描述誤差變量的詞集一般取為:負大(NB),負中(NM),負小(NS),負零(NO),正零(PO),正小(PS),正中(PM),正大(PB)。
模糊變量E的賦值表
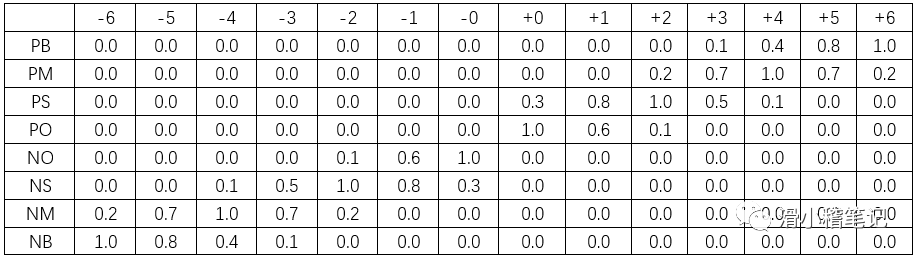
模糊控制規則
(1)條件語句的基本類型為:if A or B and C or D then E
例如水溫控制規則之一為:若水溫高或偏高,且溫度上升快或較快,則加大冷水流量。
用條件語句表達為:if E=NB or NM and EC=NB or NM then U=PB
1.2.8 模糊控制算法的工程實現
在大型的模糊控制系統中常采用軟件模糊推理法,模糊關系,模糊推理以及模糊判決的運算可以離線進行,最后得到模糊控制器輸入量的量化等級E,EC與輸出量即系統控制量的量化等級U之間的確定關系,這種關系通常稱為控制表。
1.3 水位控制系統
1.3.1 控制目標
控制模型如下圖所示,控制進水閥S1和出水閥S2,使水箱水位保持在目標水位O處。
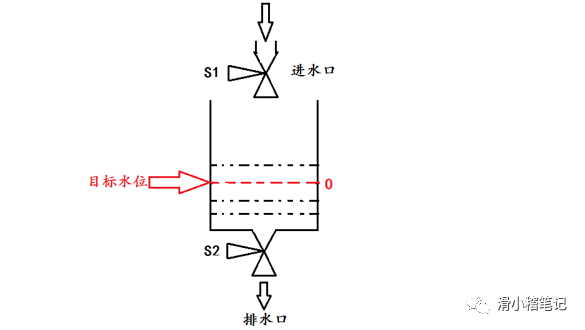
1.3.2 控制規則
(1)若當前水位高于目標水位,則向外排水,差值越大,排水越快
(2)若當前水位低于目標水位,則向內注水,差值越大,注水越快
(3)若當前水位和目標水位相差很小,則保持排水速度和注水速度相等
注:建立模糊控制規則的基本思想:當誤差大或較大時,選擇控制量應該以盡快消除誤差為主,而當誤差較小時,選擇控制量要防止超調,以系統的穩定性為主要出發點。
1.3.3 控制步驟
(1)我們選擇目標水位和當前水位的差值e作為觀察量,選取閥門開度u為控制量。
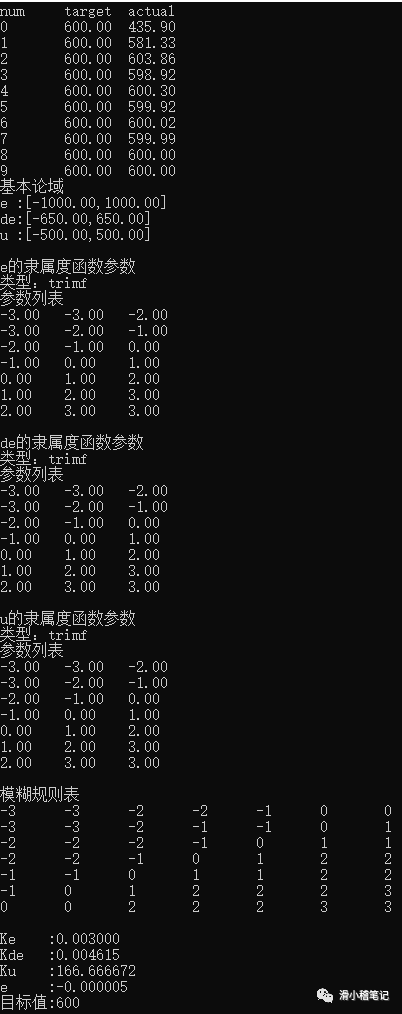
(2)將偏差e劃分為5個模糊集,負大(NB)、負小(NS)、零(ZO)、正小(PS)、正大(PB),e為負表示當前水位低于目標水位,e為正表示當前水位高于目標水位。設定e的取值范圍為[-3,3],隸屬度函數如下圖所示。
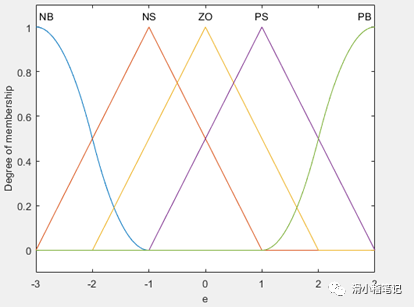
此時偏差e對應的模糊表如下表所示。
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| PB | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| PS | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
| ZO | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
| NS | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
| NB | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
(3)將控制量u劃分為5個模糊集,負大(NB)、負小(NS)、零(ZO)、正小(PS)、正大(PB),u為負表示增大進水閥門S1的開度(同時減小出水閥門S2的開度),u為正表示減小進水閥門S1的開度(同時增大出水閥門S2的開度)。設定u的取值范圍為[-4,4],隸屬度函數如下。
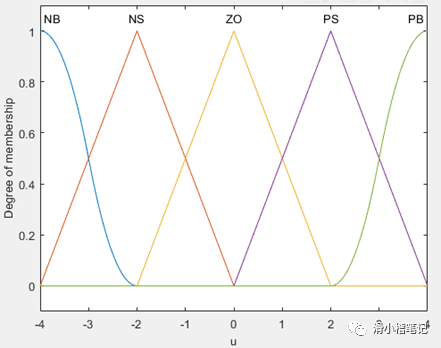
此時控制量u對應的模糊表如下表所示。
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|---|---|---|
| PB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| PS | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
| ZO | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
| NS | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| NB | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
(4)制定模糊規則:模糊規則的制定是模糊控制的核心內容,控制性能的好壞很大程度上由模糊規則決定,目前主要是根據經驗來制定相應的規則
若e負大,則u負大
若e負小,則u負小
若e為零,則u為零
若e正小,則u正小
若e正大,則u正大
(6)進行模糊決策:最終需要的控制量u即為模糊控制的輸出,u可由偏差矩陣e和模糊關系矩陣R合成得到
(7)控制量的反模糊化
我們模糊決策得到的控制量u是一個矩陣,并不能直接應用在工程上,因此需要將u解釋為實際中的特定行為,即反模糊化操作。目前常用的反模糊化方法有以下幾種:
最大隸屬度法:應用于計算簡單控制要求不高場合
重心法:可以使得輸出更平滑
加權平均法:工業上應用最廣泛
1.4 模糊控制算法實現
1.4.1 MATLAB代碼
clc
clear
%創建模糊控制器
a = newfis('fuzzy tank');
%輸入變量
a = addvar(a,'input','e',[-3,3]); %設置變量e為輸入且定義域[-3,3]
a = addmf(a,'input',1,'NB','zmf',[-3,-1]); %Z型隸屬度函數
a =addmf(a,'input',1,'NS','trimf',[-3,-1,1]); %三角形隸屬度函數
a =addmf(a,'input',1,'ZO','trimf',[-2,0,2]); %三角形隸屬度函數
a =addmf(a,'input',1,'PS','trimf',[-1,1,3]); %三角形隸屬度函數
a = addmf(a,'input',1,'PB','smf',[1,3]); %S型隸屬度函數
%輸出變量
a = addvar(a,'output','u',[-4,4]); %設置變量u為輸出且定義域[-4,4]
a = addmf(a,'output',1,'NB','zmf',[-4,-2]); %Z型隸屬度函數
a =addmf(a,'output',1,'NS','trimf',[-4,-2,0]); %三角形隸屬度函數
a =addmf(a,'output',1,'ZO','trimf',[-2,0,2]); %三角形隸屬度函數
a =addmf(a,'output',1,'PS','trimf',[0,2,4]); %三角形隸屬度函數
a = addmf(a,'output',1,'PB','smf',[2,4]); %S型隸屬度函數
%建立模糊規則
rulelist=[1 1 1 1;
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a = addrule(a,rulelist);
%設置反模糊化算法
a1 = setfis(a,'DefuzzMethod','mom'); %采用最大隸屬度平均法進行反模糊化
writefis(a1,'tank'); %保存tank文件
a2 = readfis('tank'); %讀取tank文件
%繪制圖像
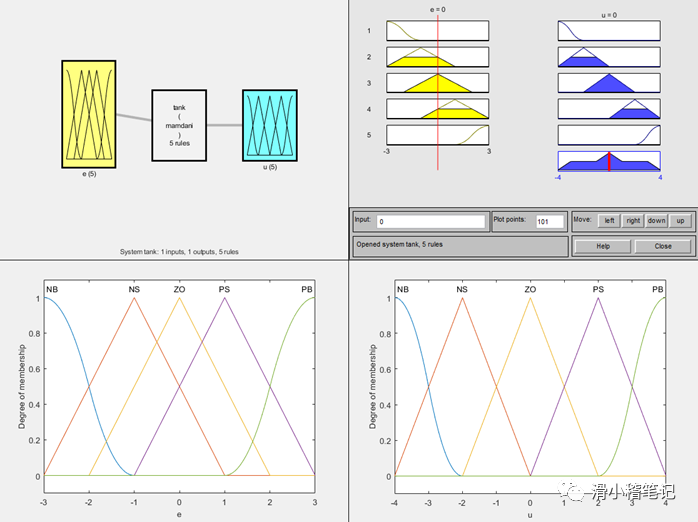
figure(1); plotfis(a2); %繪制模糊控制器結構
figure(2); plotmf(a,'input',1); %繪制輸入隸屬度函數圖像
figure(3); plotmf(a,'output',1); %繪制輸出隸屬度函數圖像
%打開模糊調試器
showrule(a);
ruleview('tank');
-
模糊控制
+關注
關注
2文章
261瀏覽量
25547 -
模糊算法
+關注
關注
0文章
16瀏覽量
8763 -
自然語言
+關注
關注
1文章
291瀏覽量
13398
發布評論請先 登錄
相關推薦
PID算法之模糊PID 精選資料推薦
PID算法學習筆記分享
基于模糊高斯學習策略的粒子群進化融合算法
基于深度學習的圖像去模糊算法及應用
MATLAB學習筆記之模糊算法1
MATLAB學習筆記之模糊算法3




 MATLAB學習筆記之模糊算法2
MATLAB學習筆記之模糊算法2











評論