本文主要介紹基于集成學習的決策樹,其主要通過不同學習框架生產基學習器,并綜合所有基學習器的預測結果來改善單個基學習器的識別率和泛化性。
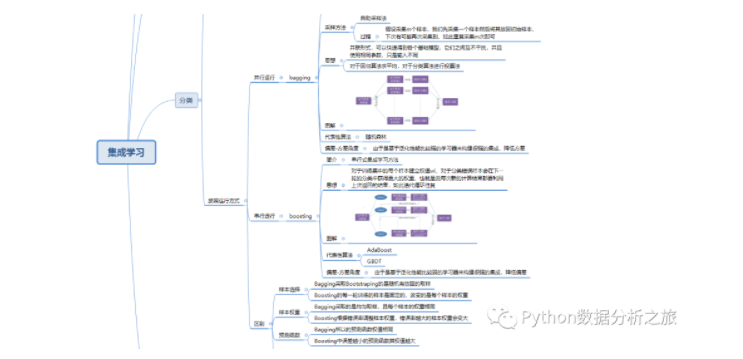
1. 集成學習
常見的集成學習框架有三種:Bagging,Boosting 和 Stacking。三種集成學習框架在基學習器的產生和綜合結果的方式上會有些區別,我們先做些簡單的介紹。
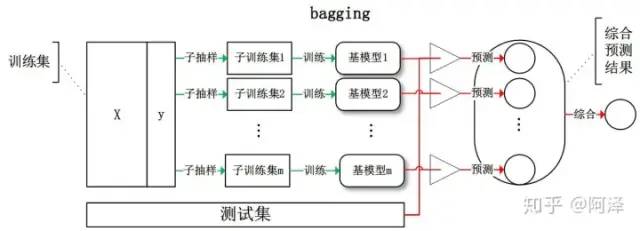
1.1 Bagging
Bagging 全稱叫 Bootstrap aggregating,看到 Bootstrap 我們立刻想到著名的開源前端框架(抖個機靈,是 Bootstrap 抽樣方法) ,每個基學習器都會對訓練集進行有放回抽樣得到子訓練集,比較著名的采樣法為 0.632 自助法。每個基學習器基于不同子訓練集進行訓練,并綜合所有基學習器的預測值得到最終的預測結果。Bagging 常用的綜合方法是投票法,票數最多的類別為預測類別。
1.2 Boosting
Boosting 訓練過程為階梯狀,基模型的訓練是有順序的,每個基模型都會在前一個基模型學習的基礎上進行學習,最終綜合所有基模型的預測值產生最終的預測結果,用的比較多的綜合方式為加權法。

1.3 Stacking
Stacking 是先用全部數據訓練好基模型,然后每個基模型都對每個訓練樣本進行的預測,其預測值將作為訓練樣本的特征值,最終會得到新的訓練樣本,然后基于新的訓練樣本進行訓練得到模型,然后得到最終預測結果。

那么,為什么集成學習會好于單個學習器呢?原因可能有三:
- 訓練樣本可能無法選擇出最好的單個學習器,由于沒法選擇出最好的學習器,所以干脆結合起來一起用;
- 假設能找到最好的學習器,但由于算法運算的限制無法找到最優解,只能找到次優解,采用集成學習可以彌補算法的不足;
- 可能算法無法得到最優解,而集成學習能夠得到近似解。比如說最優解是一條對角線,而單個決策樹得到的結果只能是平行于坐標軸的,但是集成學習可以去擬合這條對角線。
2. 偏差與方差
上節介紹了集成學習的基本概念,這節我們主要介紹下如何從偏差和方差的角度來理解集成學習。
2.1 集成學習的偏差與方差
偏差(Bias)描述的是預測值和真實值之差;方差(Variance)描述的是預測值作為隨機變量的離散程度。放一場很經典的圖:

模型的偏差與方差
- 偏差:描述樣本擬合出的模型的預測結果的期望與樣本真實結果的差距,要想偏差表現的好,就需要復雜化模型,增加模型的參數,但這樣容易過擬合,過擬合對應上圖的 High Variance,點會很分散。低偏差對應的點都打在靶心附近,所以喵的很準,但不一定很穩;
- 方差:描述樣本上訓練出來的模型在測試集上的表現,要想方差表現的好,需要簡化模型,減少模型的復雜度,但這樣容易欠擬合,欠擬合對應上圖 High Bias,點偏離中心。低方差對應就是點都打的很集中,但不一定是靶心附近,手很穩,但不一定瞄的準。
我們常說集成學習中的基模型是弱模型,通常來說弱模型是偏差高(在訓練集上準確度低)方差小(防止過擬合能力強)的模型,但并不是所有集成學習框架中的基模型都是弱模型。Bagging 和 Stacking 中的基模型為強模型(偏差低,方差高),而Boosting 中的基模型為弱模型(偏差高,方差低)。
在 Bagging 和 Boosting 框架中,通過計算基模型的期望和方差我們可以得到模型整體的期望和方差。為了簡化模型,我們假設基模型的期望為 ,方差
,方差  ,模型的權重為 r ,兩兩模型間的相關系數
,模型的權重為 r ,兩兩模型間的相關系數 相等。由于 Bagging 和 Boosting 的基模型都是線性組成的,那么有:
相等。由于 Bagging 和 Boosting 的基模型都是線性組成的,那么有:
模型總體期望:

模型總體方差(公式推導參考協方差的性質,協方差與方差的關系):

模型的準確度可由偏差和方差共同決定:

2.2 Bagging 的偏差與方差
對于 Bagging 來說,每個基模型的權重等于 1/m 且期望近似相等,故我們可以得到:

通過上式我們可以看到:
- 整體模型的期望等于基模型的期望,這也就意味著整體模型的偏差和基模型的偏差近似。
- 整體模型的方差小于等于基模型的方差,當且僅當相關性為 1 時取等號,隨著基模型數量增多,整體模型的方差減少,從而防止過擬合的能力增強,模型的準確度得到提高。 但是,模型的準確度一定會無限逼近于 1 嗎?并不一定,當基模型數增加到一定程度時,方差公式第一項的改變對整體方差的作用很小,防止過擬合的能力達到極限,這便是準確度的極限了。
在此我們知道了為什么 Bagging 中的基模型一定要為強模型,如果 Bagging 使用弱模型則會導致整體模型的偏差提高,而準確度降低。
Random Forest 是經典的基于 Bagging 框架的模型,并在此基礎上通過引入特征采樣和樣本采樣來降低基模型間的相關性,在公式中顯著降低方差公式中的第二項,略微升高第一項,從而使得整體降低模型整體方差。
2.3 Boosting 的偏差與方差
對于 Boosting 來說,由于基模型共用同一套訓練集,所以基模型間具有強相關性,故模型間的相關系數近似等于 1,針對 Boosting 化簡公式為:

通過觀察整體方差的表達式我們容易發現:
- 整體模型的方差等于基模型的方差,如果基模型不是弱模型,其方差相對較大,這將導致整體模型的方差很大,即無法達到防止過擬合的效果。因此,Boosting 框架中的基模型必須為弱模型。
- 此外 Boosting 框架中采用基于貪心策略的前向加法,整體模型的期望由基模型的期望累加而成,所以隨著基模型數的增多,整體模型的期望值增加,整體模型的準確度提高。
基于 Boosting 框架的 Gradient Boosting Decision Tree 模型中基模型也為樹模型,同 Random Forrest,我們也可以對特征進行隨機抽樣來使基模型間的相關性降低,從而達到減少方差的效果。
2.4 小結
- 我們可以使用模型的偏差和方差來近似描述模型的準確度;
- 對于 Bagging 來說,整體模型的偏差與基模型近似,而隨著模型的增加可以降低整體模型的方差,故其基模型需要為強模型;
- 對于 Boosting 來說,整體模型的方差近似等于基模型的方差,而整體模型的偏差由基模型累加而成,故基模型需要為弱模型。
?那么這里有一個小小的疑問,Bagging 和 Boosting 到底用的是什么模型呢?
3. Random Forest
Random Forest(隨機森林),用隨機的方式建立一個森林。RF 算法由很多決策樹組成,每一棵決策樹之間沒有關聯。建立完森林后,當有新樣本進入時,每棵決策樹都會分別進行判斷,然后基于投票法給出分類結果。
3.1 思想
Random Forest(隨機森林)是 Bagging 的擴展變體,它在以決策樹為基學習器構建 Bagging 集成的基礎上,進一步在決策樹的訓練過程中引入了隨機特征選擇,因此可以概括 RF 包括四個部分:
- 隨機選擇樣本(放回抽樣);
- 隨機選擇特征;
- 構建決策樹;
- 隨機森林投票(平均)。
隨機選擇樣本和 Bagging 相同,采用的是 Bootstrap 自助采樣法;隨機選擇特征是指在每個節點在分裂過程中都是隨機選擇特征的(區別與每棵樹隨機選擇一批特征)。
這種隨機性導致隨機森林的偏差會有稍微的增加(相比于單棵不隨機樹),但是由于隨機森林的“平均”特性,會使得它的方差減小,而且方差的減小補償了偏差的增大,因此總體而言是更好的模型。
隨機采樣由于引入了兩種采樣方法保證了隨機性,所以每棵樹都是最大可能的進行生長就算不剪枝也不會出現過擬合。
3.2 優缺點
優點
- 在數據集上表現良好,相對于其他算法有較大的優勢
- 易于并行化,在大數據集上有很大的優勢;
- 能夠處理高維度數據,不用做特征選擇。
4 Adaboost
AdaBoost(Adaptive Boosting,自適應增強),其自適應在于:前一個基本分類器分錯的樣本會得到加強,加權后的全體樣本再次被用來訓練下一個基本分類器。同時,在每一輪中加入一個新的弱分類器,直到達到某個預定的足夠小的錯誤率或達到預先指定的最大迭代次數。
4.1 思想
Adaboost 迭代算法有三步:
- 初始化訓練樣本的權值分布,每個樣本具有相同權重;
- 訓練弱分類器,如果樣本分類正確,則在構造下一個訓練集中,它的權值就會被降低;反之提高。用更新過的樣本集去訓練下一個分類器;
- 將所有弱分類組合成強分類器,各個弱分類器的訓練過程結束后,加大分類誤差率小的弱分類器的權重,降低分類誤差率大的弱分類器的權重。
-
集成學習
+關注
關注
0文章
10瀏覽量
7333 -
機器學習
+關注
關注
66文章
8438瀏覽量
133084 -
決策樹
+關注
關注
3文章
96瀏覽量
13587
發布評論請先 登錄
相關推薦




 基于集成學習的決策介紹(上)
基于集成學習的決策介紹(上)
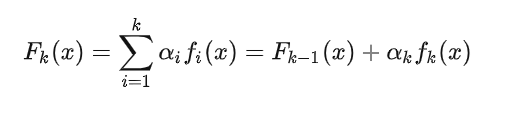











評論