先大致講一下什么是深度學(xué)習(xí)中優(yōu)化算法吧，我們可以把模型比作函數(shù)，一種很復(fù)雜的函數(shù)：h(f(g(k(x))))，函數(shù)有參數(shù)，這些參數(shù)是未知的，深度學(xué)習(xí)中的“學(xué)習(xí)”就是通過(guò)訓(xùn)練數(shù)據(jù)求解這些未知的參數(shù)。

由于這個(gè)函數(shù)太復(fù)雜了，沒(méi)辦法進(jìn)行直接求解，所以只能換個(gè)思路：衡量模型的輸出與真實(shí)標(biāo)簽之間的差距，如果差距過(guò)大，則調(diào)整模型參數(shù)，然后重新計(jì)算差距，如此反復(fù)迭代，直至差距在接受范圍內(nèi)。

深度學(xué)習(xí)中通過(guò)目標(biāo)函數(shù)或者損失函數(shù)衡量當(dāng)前參數(shù)的好壞，而調(diào)整模型參數(shù)的就是優(yōu)化算法。

所謂優(yōu)化， 就是利用關(guān)于最優(yōu)解的信息，不斷逼近最優(yōu)解， 目前深度學(xué)習(xí)中最常用的是梯度下降法， 梯度方向就是最優(yōu)解的信息，因?yàn)樘荻确较蛑赶蜃顑?yōu)解方向， 沿著梯度方向前進(jìn)即可靠近最優(yōu)解。

到這里，你是不是覺(jué)得優(yōu)化算法很簡(jiǎn)單？其實(shí)，不然。讓我們進(jìn)一步分析。

難點(diǎn)一：梯度（困難指數(shù)兩顆星）

所謂梯度下降法，當(dāng)然要計(jì)算梯度，前面那個(gè)復(fù)合函數(shù)再加上損失函數(shù)，最終要優(yōu)化的函數(shù)是這個(gè)樣子：L(h(f(g(k(x)))),y)，L是損失函數(shù)，y是標(biāo)簽值。

復(fù)合函數(shù)通過(guò)鏈?zhǔn)椒▌t進(jìn)行求導(dǎo)，例如f(g(x))，

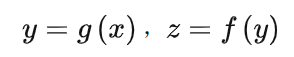
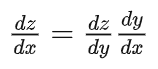
這就要求g(x)和f(x)都得可導(dǎo)，對(duì)于神經(jīng)網(wǎng)絡(luò)而言，卷積層和全連接層都可以看作是矩陣與向量乘法，是可導(dǎo)的，剩下的就是激活函數(shù)和損失函數(shù)，好在目前常用的MSE，交叉熵?fù)p失函數(shù)，Sigmoid，Relu激活函數(shù)都是可導(dǎo)的。

所以，梯度的問(wèn)題不大。

難點(diǎn)二：凸優(yōu)化和非凸優(yōu)化（ 困難指數(shù)五顆星 ）

深度學(xué)習(xí)由于多個(gè)隱藏層的疊加所形成的復(fù)合函數(shù)，外加損失函數(shù)，最終的函數(shù)往往不是凸函數(shù)。

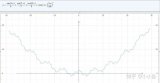
所謂凸函數(shù)，就是只有全局最優(yōu)解，通過(guò)梯度下降最終都能找到這個(gè)最優(yōu)解，對(duì)于機(jī)器學(xué)習(xí)中的線(xiàn)性回歸的損失函數(shù)：最小二乘而言，它是一個(gè)凸函數(shù)，也就是說(shuō)能找到使損失函數(shù)達(dá)到最小值的全局最優(yōu)解。

在非凸函數(shù)中，存在大量的局部最優(yōu)解，局部極值隨著特征維度的增加呈指數(shù)增長(zhǎng)，優(yōu)化算法很大概率找不到全局最優(yōu)解，這也是優(yōu)化算法最苦惱的地方。

如果只有局部最優(yōu)解，那情況還不算最糟糕，畢竟局部最優(yōu)解意味著從所有維度看都是最小值或者最大值，更糟糕的是鞍點(diǎn)，這種情況雖然一階導(dǎo)數(shù)都為零，但二階導(dǎo)數(shù)不同向，也就是說(shuō)從某些維度看是極小值，而從某些維度看卻是極大值。

而且，不幸的是，隨著特征向量維度的增加，鞍點(diǎn)的數(shù)量也是隨著指數(shù)級(jí)增加的。

那如何逃離鞍點(diǎn)？

這里再次注意：這里我們所說(shuō)的梯度下降指的是：使用全部樣本的損失的平均值來(lái)更新參數(shù)，這就意味著梯度的精度非常高，會(huì)精確地逼近鞍點(diǎn)，但我們不希望這樣，我們希望能夠跳出鞍點(diǎn)，幸好，隨機(jī)梯度下降SGD或者其變體（比如Momentun、Adam、mini-batch）的出現(xiàn)很大程度上解決了該問(wèn)題。

例如，mini-batch是指每次參數(shù)更新只是用一小批樣本，這是一種有噪聲的梯度估計(jì)，哪怕我們位于梯度為0的點(diǎn)，也經(jīng)常在某個(gè)mini-batch下的估計(jì)把它估計(jì)偏了，導(dǎo)致往前或者往后挪了一步摔下馬鞍，也就是mini-batch的梯度下降法使得模型很容易逃離特征空間中的鞍點(diǎn)。

既然，局部極值點(diǎn)也可接受，且又能有方法逃離鞍點(diǎn)，到這里你覺(jué)得問(wèn)題就結(jié)束了嗎？還沒(méi)有，其實(shí)，神經(jīng)網(wǎng)絡(luò)中最讓人望而生畏的不是局部最優(yōu)點(diǎn)和鞍點(diǎn)，而是平坦地區(qū)，這些地區(qū)一經(jīng)進(jìn)入很難逃離。

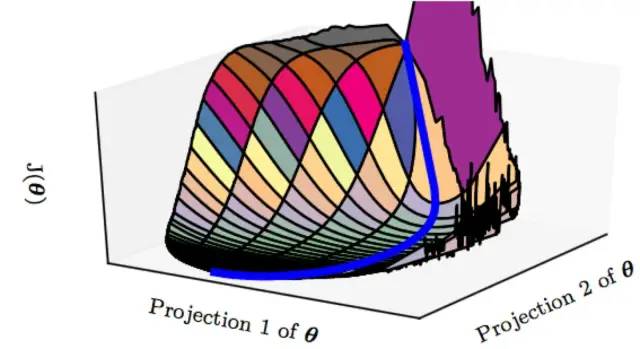
總結(jié)來(lái)說(shuō)，人們認(rèn)為的深度神經(jīng)網(wǎng)絡(luò)“容易收斂到局部最優(yōu)”，很可能是一種想象，實(shí)際情況是，我們可能從來(lái)沒(méi)有找到過(guò)“局部最優(yōu)”，更別說(shuō)全局最優(yōu)了。

所以，與其擔(dān)憂(yōu)陷入局部最優(yōu)點(diǎn)怎么跳出來(lái)，更不如去考慮數(shù)據(jù)集要怎么做才能讓網(wǎng)絡(luò)更好學(xué)習(xí)，以及網(wǎng)絡(luò)該怎么設(shè)計(jì)才能更好的捕獲pattern，網(wǎng)絡(luò)該怎么訓(xùn)練才能學(xué)到我們想讓它學(xué)習(xí)的知識(shí)。

最后，也要為優(yōu)化算法鳴個(gè)不平。其實(shí)這并不是優(yōu)化算法的問(wèn)題。是損失函數(shù)和網(wǎng)絡(luò)結(jié)構(gòu)的錯(cuò)，是他們的復(fù)雜性導(dǎo)致優(yōu)化問(wèn)題是一個(gè)非凸優(yōu)化問(wèn)題，優(yōu)化算是是來(lái)解決問(wèn)題的，而不是制造問(wèn)題。