電阻反饋網絡通常用于設置電源的輸出電壓。機械電位器（電位器）方便地解決了調節電源的問題。為了便于自動校準，可以用數字電位器代替機械電位器。本應用筆記介紹了一種使用數字電位器的校準解決方案，因為數字電位器更小，不會隨著年齡或振動而移動，并且可以遠程重新校準。該解決方案降低了系統對數字電位器端到端電阻容差的敏感性，使該解決方案成為設計人員的最佳選擇。本應用筆記還解釋了計算電阻鏈值和以這種方式使用數字電位器所需的一些公式。提供具有標準 reisistor 值的電子表格，以便于計算。

介紹

電阻反饋網絡通常用于設置電源的輸出電壓，因為固定電阻器易于使用且成本低。但是，由于固定網絡不可調，因此無法準確設置輸出電壓。因此，許多電源在反饋網絡中使用機械電位器（電位器）來設置輸出電壓。為了便于自動校準，可以用數字電位計代替機械電位計。數字電位計更小，不會隨著年齡或振動而顯著移動，甚至可以遠程重新校準。本應用筆記解釋了以這種方式使用數字電位器所需的一些計算，并提供了一個電子表格，以便于計算。

常規電源反饋

電源通常使用阻性反饋來設置輸出電平。然而，由于器件容差很多，都會影響輸出電壓，因此固定電阻分壓器通常是不夠的。在這些情況下，使用可變電阻比，以便在最終測試中校準系統。

雖然傳統上會使用機械電位計，但在許多應用中，這些元件已被數字電位計所取代。數字電位器不會受到明顯的老化影響，并且在最終測試中自動調整要簡單得多。

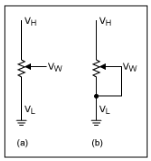
固定電阻和機械電位計方案如圖1和圖2所示。

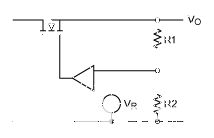
圖1.傳統的固定電阻反饋。

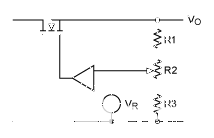
圖2.傳統的可變電阻反饋。

以具有2.5V基準電壓的12V電源的典型示例為例。基準電壓和系統中的所有其他器件將具有容差。方便的是，所有公差都可以表示為基準上的附加公差。在本例中，我們將使用 ±5% 的典型總公差作為參考。

計算固定電阻反饋的值基于一個簡單的公式：

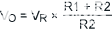（公式1）

由于在此示例中，VR將具有 ±5% 的容差，這導致輸出電壓的容差為 5%。如果這在應用中不可接受，則需要使電阻分壓器可變。通常不會用機械電位計代替R1和R2，因為這會導致輸出電壓范圍很寬，并且對調整非常敏感。隨著時間的推移和溫度，電位器位置的任何漂移都會產生不可接受的輸出電壓漂移。因此，圖2展示了一種減小輸出范圍的方案，現在更容易調整，也更穩定。

假設，我們應該能夠用數字電位器代替R2，并且我們應該有一個電動可調系統。然而，事情并沒有那么簡單。首先，需要對數字電位器進行一些解釋。

數字電位器的基本結構

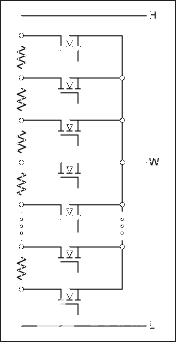
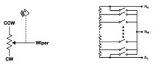
圖3.典型的數字電位計結構。

數字電位器通常是一串電阻，每個節點都有一個開關，如圖3所示。為簡單起見，這些開關顯示為單個MOSFET。通常，這些開關將是兩個BiCMOS晶體管（一個“P”和一個“N”），以產生低導通電阻。

這種結構通常用于多達 256 個水龍頭的鍋。當電位器高于 256 個抽頭時，使用更復雜的分段結構可能更有效。但是，這超出了本應用說明的范圍。

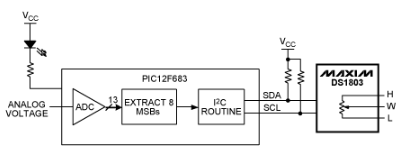
由于所有電阻器都在同一芯片上制造，因此它們將非常緊密地匹配。不幸的是，端到端電阻可能沒有那么明確定義。典型的數字電位器是MAX5402，這是一款單通道、256抽頭器件，端到端電阻為10kΩ （典型值）。然而，端到端電阻容差為±20%。在比率學上，它的定義要好得多，積分非線性（INL）為0.5 LSB（最大值）。因此，它非常適合用作電位分隔器。

使用數字電位器校準電源

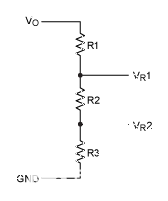
圖4.初始電阻串。

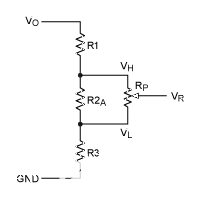
圖5.最終電阻串。

電阻值R1、R2和R3的計算方法如圖4所示。我們將使用以下示例：

VO= 12V
VR= 2.5V ±5%
RT= R1 + R2 + R3

初始方程很簡單，定義如下：

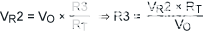（公式2）

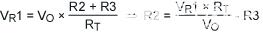（公式3）

第一步是定義 R 的總電阻T，使用 （R1 + R2 + R3）。由于這是任意的，我們將從 R 開始T= 20kΩ。（如果需要，我們以后可以隨時更改它，以便為 R1、R2 和 R3 提供更真實的值。從公式2中，我們發現R3 = 3.598kΩ。根據公式3，R2 = 417Ω，從公式4，R1 = 15.625kΩ。

顯然，計算出的理想電阻值通常不可用，因此需要使用標準電阻值。最接近的1%值替換為R1和R3：R1 = 15.8kΩ，R3 = 3.92kΩ。（為方便起見，我們在電子表格中包含了標準電阻值圖表。

現在我們可以向后計算以找到R2的理想值，如公式5所示。R2 最終將變為可變值。因此，計算其值，以便 VO當 R2 傾斜且 V 傾斜時將是正確的R是其標稱值。

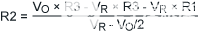（公式5）

因此，R2 = 646Ω。

我們需要考慮到這樣一個事實，即數字電位器的端到端容差非常差。將大值數字電位器與小值固定電阻并聯是降低電位器端到端容差差影響的簡單方法。如圖 5 所示。因此，R2的并聯組合一個和 RP生成 R2。

使用公式6，最后一步是計算并聯固定電阻的值，給定一個電位計標稱端到端電阻。

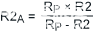（公式6）

因此，使用10kΩ電位器進行RP，R2 的理想值一個為690Ω。最接近的1%值為698Ω。如果我們計算這個和數字電位器在其公差極值下的并聯組合，我們得到R最低= 642Ω 和 R.MAX= 660Ω.由于鍋的端到端公差為20%，因此公差僅為1%。我們使用698Ω電阻作為R2一個，因為這是最接近的標準 1% 值。

最終計算證實，使用實際值時，數字電位器可以覆蓋基準電壓源容差所需的5%范圍。我們可以使用星三角變換，如圖 6 所示。我們顯然不需要計算 R6。

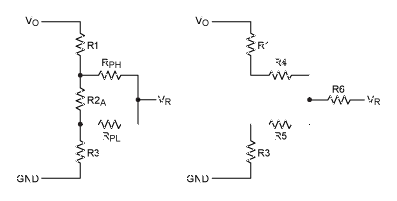
圖6.使用星三角變換。

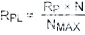（公式7）

其中 N 是抽頭位置，NMAX 是最大抽頭位置。

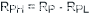（公式8）

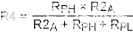（公式9）

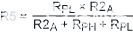（公式10）

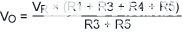（公式11）

使用這些公式，我們確認電位器的范圍將涵蓋參考的公差范圍。

要匯總要求和所選組件值，請執行以下操作：

VO= 12V （輸出電壓）
VR= 2.5V ±5% （基準電壓） R1 = 15.8kΩ （上部電阻）
R1 = 15.8kΩ (upper resistor)
R2一個= 698Ω （并聯電阻）
RP= 10kΩ （數字電位計） R3 = 3.92kΩ （下電阻）
R3 = 3.92kΩ (lower resistor)

以下抽頭點將所需的輸出電壓設置在基準容差的極端值。

VR= 2.375V， 抽頭 = 44， VO= 11.99842V
VR= 2.625V，抽頭 = 210，VO= 11.99773V

可以進一步優化以降低輸出電壓階躍。但是，電位計在兩端確實有一些開銷，以考慮任何進一步的容差。

總結

本應用筆記討論了調整電源的問題，以及如何使用機械電位器解決這個問題。此外，本文還介紹了使用數字電位器的校準解決方案，因為數字電位器更小，不會隨著年齡或振動而移動，并且可以遠程重新校準。該解決方案還降低了數字電位計端到端電阻的容差，使該解決方案成為設計人員的最佳選擇。開發了計算電阻鏈值所需的公式，并提供了包含標準電阻值圖表的電子表格。

審核編輯：郭婷