傅里葉級數在數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學等領域都有著廣泛的應用，這不由得讓人肅然起敬。

一打開《信號與系統》、《鎖相環原理》等書籍，動不動就跳出一個“傅里葉級數”或“傅里葉變換”，弄一長串公式，讓人云山霧罩。

如下就是傅里葉級數的公式：

不客氣地說，這個公式可以說是像“臭婆娘的裹腳布——又臭又長”，而且來歷相當蹊蹺，不知那個傅里葉什么時候靈光乍現，把一個周期函數f(t)硬生生地寫成這么一大堆東西。

單看那個①式，就是把周期函數f(t)描述成一個常數系數a0、及1倍ω的sin和cos函數、2倍ω的sin和cos函數等、到n倍ω的sin和cos函數等一系列式子的和，且每項都有不同的系數，即An和Bn，至于這些系數，需要用積分來解得，即②③④式，不過為了積分方便，積分區間一般設為[-π, π]，也相當一個周期T的寬度。

能否從數學的角度推導出此公式，以使傅里葉級數來得明白些，讓我等能了解它的前世今生呢?下面來詳細解釋一下此公式的得出過程：

1、把一個周期函數表示成三角級數：

首先，周期函數是客觀世界中周期運動的數學表述，如物體掛在彈簧上作簡諧振動、單擺振動、無線電電子振蕩器的電子振蕩等，大多可以表述為：

f(x)=A sin(ωt+ψ)

這里t表示時間，A表示振幅，ω為角頻率，ψ為初相(與考察時設置原點位置有關)。

然而，世界上許多周期信號并非正弦函數那么簡單，如方波、三角波等。傅葉里就想，能否用一系列的三角函數An sin(nωt+ψ)之和來表示那個較復雜的周期函數f(t)呢?因為正弦函數sin可以說是最簡單的周期函數了。于是，傅里葉寫出下式：(關于傅里葉推導純屬猜想)

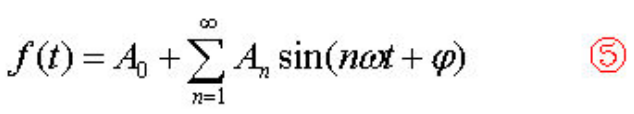
這里，t是變量，其他都是常數。與上面最簡單的正弦周期函數相比，5式中多了一個n，且n從1到無窮大。這里f(t)是已知函數，也就是需要分解的原周期函數。從公式5來看，傅里葉是想把一個周期函數表示成許多正弦函數的線性疊加，這許許多多的正弦函數有著不同的幅度分量(即式中An)、有不同的周期或說是頻率(是原周期函數的整數倍，即n)、有不同的初相角(即ψ)，當然還有一項常數項(即A0)。要命的是，這個n是從1到無窮大，也就是是一個無窮級數。

應該說，傅里葉是一個天才，想得那么復雜。一般人不太會把一個簡單的周期函數弄成這么一個復雜的表示式。但傅里葉認為，式子右邊一大堆的函數，其實都是最簡單的正弦函數，有利于后續的分析和計算。當然，這個式能否成立，關鍵是級數中的每一項都有一個未知系數，如A0、An等，如果能把這些系數求出來，那么5式就可以成立。當然在5式中，唯一已知的就是原周期函數f(t),那么只需用已知函數f(t)來表達出各項系數，上式就可以成立，也能計算了。

于是乎，傅里葉首先對式5作如下變形：

這樣，公式5就可以寫成如下公式6的形式：

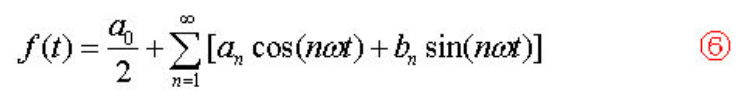
這個公式6就是通常形式的三角級數，接下來的任務就是要把各項系數an和bn及a0用已知函數f(t)來表達出來。

2、三角函數的正交性：

這是為下一步傅里葉級數展開時所用積分的準備知識。一個三角函數系：1，cosx , sinx , cos2x , sin2x , … , cosnx , sinnx , … 如果這一堆函數(包括常數1)中任何兩個不同函數的乘積在區間[-π, π]上的積分等于零，就說三角函數系在區間[-π, π]上正交，即有如下式子：

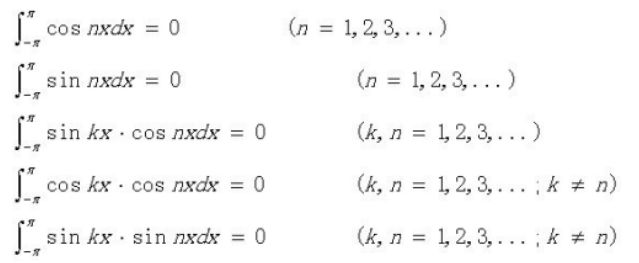
以上各式在區間[-π, π]的定積分均為0，第1第2式可視為三角函數cos和sin與1相乘的積分;第3-5式則為sin和cos的不同組合相乘的積分式。除了這5個式子外，不可能再有其他的組合了。注意，第4第5兩個式中，k不能等于n，否則就不屬于“三角函數系中任意兩個不同函數”的定義了，變成同一函數的平方了。但第3式中，k與n可以相等，相等時也是二個不同函數。下面通過計算第4式的定積分來驗證其正確性，第4式中二函數相乘可以寫成：

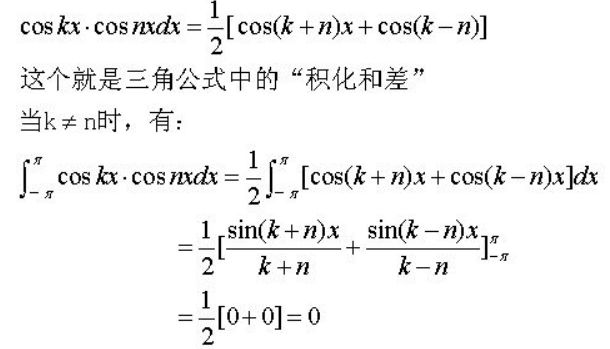
可見在指定[-π, π]的區間里，該式的定積分為0。其他式也可逐一驗證。

3、函數展開成傅里葉級數：

先把傅里葉級數表示為下式，即⑥式：

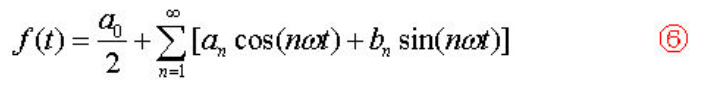
對⑥式從[-π, π]積分，得：

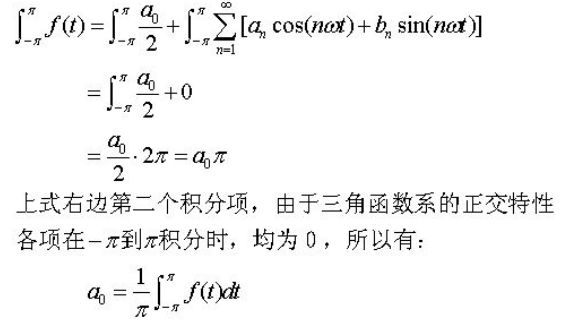
這就求得了第一個系數a0的表達式，即最上邊傅里葉級數公式里的②式。接下來再求an和bn的表達式。用cos(kωt)乘⑥式的二邊得：

至此，已經求得傅里葉級數中各系數的表達式，只要這些積分都存在，那么⑥式等號右側所表示的傅里葉級數就能用來表達原函數f(t)。上述過程就是整個傅里葉級數的推導過程。事實上，如果能夠寫出⑥式，不難求出各個系數的表達式，關鍵是人們不會想到一個周期函數竟然可以用一些簡單的正弦或余弦函數來表達，且這個表達式是一個無窮級數。這當然就是數學家傅里葉的天才之作了，我等只有拼命理解的份了。

綜上，傅里葉級數的產生過程可以分為以下三步：

1、設想可以把一個周期函數f(t)通過最簡單的一系列正弦函數來表示，即5式;

2、通過變形后用三角級數(含sin和cos)來表示;

3、通過積分，把各未知系數用f(t)的積分式來表達;

4、最后得到的4個表達式就是傅里葉級數公式。

在電子學中，傅里葉級數是一種頻域分析工具，可以理解成一種復雜的周期波分解成直流項、基波(角頻率為ω)和各次諧波(角頻率為nω)的和，也就是級數中的各項。一般，隨著n的增大，各次諧波的能量逐漸衰減，所以一般從級數中取前n項之和就可以很好接近原周期波形。這是傅里葉級數在電子學分析中的重要應用。

審核編輯：劉清