介紹
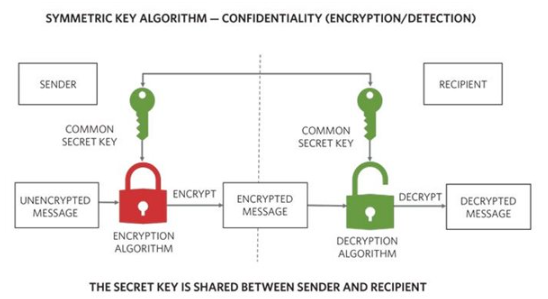
在我們的密碼學系列教程的最后兩期中,我們介紹了密碼學的基本概念和兩種基本類型。本節討論最常見的加密算法的具體實現細節,從基本的 XOR 函數開始,然后進入當今使用的更復雜的對稱和非對稱算法。本文最后回顧了如何使用非對稱密鑰算法來交換共享私鑰。這使得可以使用更快的對稱密鑰算法來交換批量加密的數據,而無需開發復雜的密鑰交換系統。
異或函數:至關重要的邏輯運算
XOR(異或)是一種重要的邏輯操作,在許多(如果不是全部)加密算法中以各種方式使用。圖 1 顯示了此函數的工作原理。在深入研究算法之前,您需要了解此函數。
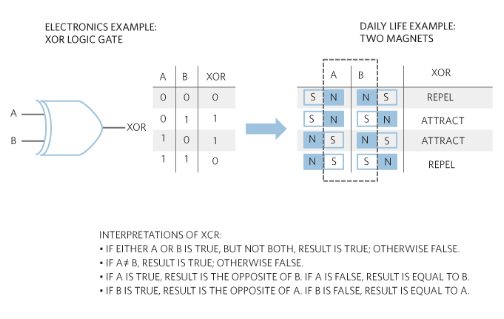
圖1.此圖顯示了 XOR 函數的工作原理。
獨占或(XOR) – 可逆(即無損)加密的基本要素
由于 XOR 的屬性,其中一個輸入可以用作進入另一個輸入的數據的鍵。例如,如果 A 是加密密鑰的單個位,則具有來自 B 的數據位的 XOR 在 A 為 1 時翻轉該位。這可以通過再次使用密鑰對加密結果進行按位 XOR 來逆轉。
讓我們看一個例子:
我們的目標是使用“秘密”這個詞,使用XOR使用密鑰對其進行加密,然后使用相同的密鑰和XOR函數對其進行解密。這些是步驟:
選擇一個密鑰。我們將選擇字母“k”作為我們的鍵。
使用 ASCII(美國信息交換標準代碼)字符編碼標準將字母“k”轉換為二進制。其結果是 :01101011
將單詞“機密”轉換為二進制。其結果是 :01010011 01100101 01100011 01110010 01100101 01110100
XOR “秘密”中的每個字母,其中“k”是關鍵字母。這為我們提供了加密值。
| S | e | c | r | e | t |
| 01010011 | 01100101 | 01100011 | 01110010 | 01100101 | 01110100 |
XOR “密鑰”:01101011 01101011 01101011 01101011 01101011 01101011
加密值:00111000 00001110 00001000 00011001 00001110 00011111
現在要解密加密值,我們使用密鑰字母“k”對其進行 XOR 運算。這一步讓我們恢復了原來的“秘密”字。
加密值:00111000 00001110 00001000 00011001 00001110 00011111
XOR “密鑰”:01101011 01101011 01101011 01101011 01101011 01101011
| 解密值: | 01010011 | 01100101 | 01100011 | 01110010 | 01100101 | 01110100 |
| S | e | c | r | e | t |
SHA(安全哈希算法)
SHA 函數背后的基本思想是獲取可變大小的數據并將其壓縮為固定大小的位字符串輸出。這個概念稱為哈希。SHA 函數是一系列哈希算法,通過 NIST(美國國家標準與技術研究院)的監督隨著時間的推移而開發。SHA-3功能是最新的。
圖 2 顯示了安全哈希生成的基本概念。
圖2.此圖顯示了安全哈希生成的基本概念。
SHA 函數具有以下特征:
可變輸入長度。
固定輸出長度。
單向功能。在圖 2 中,除了嘗試每個可能的輸入文本之外,不可能使用生成的哈希值來重新生成輸入文本。對于足夠大的輸入,這在計算上變得不可能。
如果將相同的輸入消息饋送到 SHA 函數,它將始終生成相同的結果哈希。
使用兩個不同的輸入值無法生成相同的哈希值。這稱為“防撞性”。
輸入值的微小變化,即使是單個位,也會完全改變生成的哈希值。這就是所謂的“雪崩效應”。
如果哈希函數滿足上述所有條件,則將其視為強哈希函數。
目前使用的一些 SHA 函數包括:
SHA-1
SHA-2
SHA-3
現在讓我們探討一下 SHA 函數的工作原理,重點是 SHA-2 和 SHA-3。SHA-1正在逐步淘汰,不建議用于任何新設計。
SHA-2的來龍去脈
SHA-2 函數根據輸出位長度有四種主要類型:
SHA-224 – 哈希長度為 224 位。
SHA-256 – 哈希長度為 256 位。
SHA-384 – 哈希長度為 384 位。
SHA-512 – 哈希長度為 512 位。
讓我們以 SHA-256 為例。圖 3 顯示了 SHA-256 發動機的框圖。
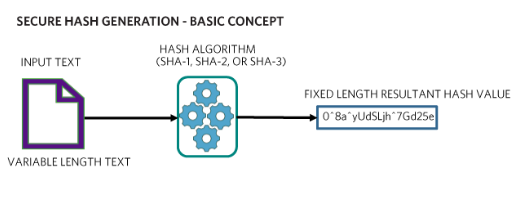
圖3.此圖顯示了用于安全哈希生成的 SHA-256 函數的框圖。
安全哈希生成:SHA-256 功能
首先填充輸入消息,以確保它完全適合“n”個 512 位塊。然后,第一個 512 位塊與初始 256 位哈希值一起輸入壓縮函數。壓縮函數基本上將消息洗牌 64 次,然后將其壓縮到 256 位并將其發送到下一個壓縮塊或作為最終哈希發送出去。因此,變量輸入消息會被多次打亂,以防止它被用來獲取原始消息。完成此操作后,將生成輸出哈希。
SHA-3 的工作原理
SHA-3 函數沒有預定義的輸出長度。輸入和輸出長度也沒有最大值。但為了與 SHA-2 進行比較,讓我們根據輸出位長度定義四種主要類型。這些是:
SHA3-224 – 哈希長度為 224 位。
SHA3-256 – 哈希長度為 256 位。
SHA3-384 – 哈希長度為 384 位。
SHA3-512 – 哈希長度為 512 位。
讓我們以 SHA3-256 為例。SHA-3使用Keccak海綿功能。就像海綿一樣,第一步吸收或吸收輸入信息。在下一階段,輸出哈希被擠出。圖 4 是 SHA3-256 函數的框圖。
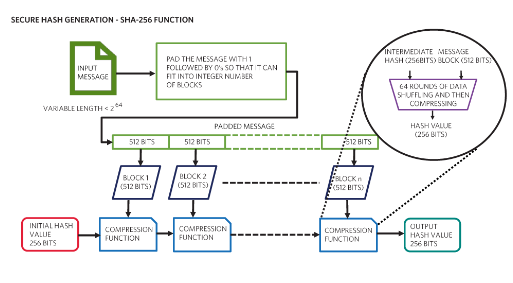
圖4.此圖顯示了用于安全哈希生成的 SHA3-256 函數的框圖。
安全哈希生成:SHA3-256 函數
圖 4 中的迭代函數接收 1600 位數據,然后使用特定算法對其進行 24 輪排列,然后將其作為 1600 位塊傳遞到下一階段。這種情況一直持續到吸收階段完成。
吸收階段完成后,最后一個 1600 位塊將傳遞到壓縮階段。在這種情況下,由于 SHA3-256 輸出哈希長度小于 1088 位,因此壓縮階段不需要任何迭代函數。我們從最后階段獲取前 256 位,這就是輸出哈希。
例如,如果所需的哈希長度為 2500 位,我們將需要迭代函數的三個實例才能獲得所需的長度哈希。
AES(高級加密標準)
與 DES(數據加密標準)和 3DES(三重數據加密標準)等舊加密算法一樣,AES 算法的目的是以可逆方式根據輸入鍵的值對輸入數據進行加擾和替換。結果稱為密文。AES算法旨在取代前幾十年開發的DES和3DES算法,這些算法容易受到攻擊。AES 算法的說明如圖 5 所示。
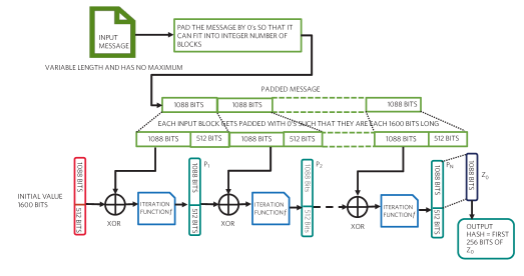
圖5.此圖概述了 AES 算法。
AES 算法
AES 算法是一種固定寬度的加密算法。因此,首先填充輸入消息,以確保它完全適合“n”個 128 位塊。
每個 128 位塊與加密密鑰一起輸入加密算法。根據加密密鑰中的位數,AES 算法執行一定數量的回合來掩蓋輸入塊位。這種模糊是通過打亂數據位、獲取部分數據并用查找表(如解碼器輪)中的值替換它們來實現的,然后執行 XOR 操作以根據從輸入加密密鑰生成的一組“圓形密鑰”中的位值將位從 0 翻轉為 1。輪次密鑰用于其中一個模糊輪次,并通過復制位并將副本插入其他位來“擴展”加密密鑰的一部分來創建。
AES解密功能只是使用相同的加密密鑰執行與加密功能中的操作相反的操作,以便對原始輸入塊數據進行解密。
3DES(三重數據加密標準)
三重 DES(或 3DES)算法背后的基本思想是根據輸入鍵的值以可逆的方式對輸入數據進行加擾和替換。結果稱為密文。3DES 算法是 1970 年代開發的原始 DES(數據加密標準)算法的重演。當 DES 在 1990 年代遭到入侵時,對更安全算法的需求是顯而易見的。3DES成為單個DES問題的近期解決方案。為了理解 3DES,圖 6 首先顯示了原始 DES 的描述。
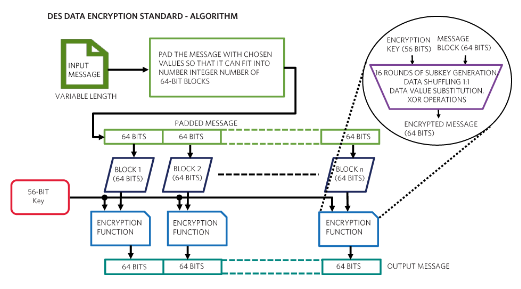
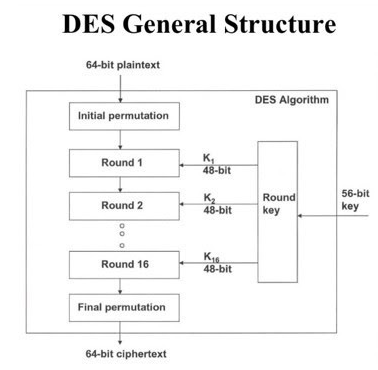
圖6.此圖概述了 DES 算法。
DES(數據加密標準)算法
DES 算法是一種固定寬度的加密算法。因此,首先填充輸入消息,以確保它完全適合“n”個 64 位塊。
每個 64 位塊與 56 位加密密鑰一起輸入加密算法(該算法的大多數版本采用 64 位密鑰,但忽略 8 位)。加密功能使用輸入密鑰生成 16 個“子密鑰”,每個子密鑰用于 16 輪遮蓋輸入塊位。這種模糊是通過打亂數據位、獲取部分數據并用查找表(如解碼器輪)中的值替換它們來實現的,然后執行 XOR 操作以根據子鍵中的位值將位從 0 翻轉到 1。
DES 解密函數只是使用相同的加密密鑰執行與加密函數中的操作相反的操作,以解密原始輸入塊數據。
3DES 如何工作?
從 DES 導出三重 DES 算法
在 DES 被證明容易受到比“暴力攻擊”(循環遍歷每個可能的密鑰值直到顯示原始消息塊)短的攻擊后,開發了一種有效增加加密密鑰大小的簡單方法。圖 7 描述了 3DES 解決方案。
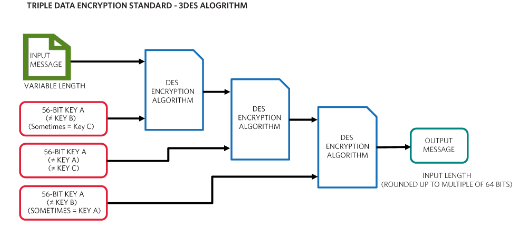
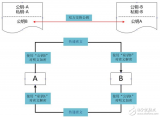
圖7.此圖顯示了如何使用三個 DES 操作來創建 3DES 算法。
3DES 算法實際上是 3 個 DES 操作。第一個和最后一個操作是加密操作,而中間操作是解密操作。請務必注意,“加密”和“解密”只是分配給彼此相反的加擾操作的名稱。
對于在 3DES 中執行的每個 DES 操作,該操作都使用專用密鑰。通常,第一個和第三個操作的鍵是相同的。對第一個和第三個操作使用相同的密鑰,對中間操作使用不同的密鑰,有效地使總密鑰長度加倍,這使得暴力攻擊更加困難,并消除了單個 DES 的漏洞。
RSA 公鑰密碼系統
RSA以其創建者Ron Rivest,Adi Shamir和Leonard Adleman的名字命名,是最早的非對稱公鑰加密/解密系統之一。它使用素數的模塊化算法的屬性來生成可用于加密的公鑰和可用于解密的私鑰。加密和解密操作也基于模塊化算法。RSA 的概述如圖 8 所示。
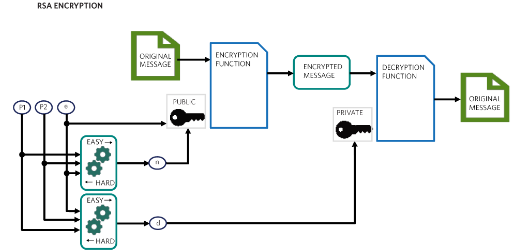
圖8.此圖顯示了 RSA 加密的概述。
密鑰生成和加密/解密操作稱為單向或“陷門”函數。它們是在一個方向上計算相對簡單的數學運算,但在另一個方向上很難計算。例如,計算乘以 2 很容易,但計算 x 的平方根更難。
在 RSA 的情況下,兩個大的素數相乘以創建公鑰和私鑰的一部分。乘法很容易;回去發現秘密素數是很困難的。
使用公鑰加密消息也比嘗試反向獲取沒有私鑰的消息要容易得多。但是,私鑰也可以輕松解鎖消息,因此絕不能共享。
私鑰可以被視為打開一個活板門,揭示了繞過試圖破解加密消息的復雜迷宮的捷徑。
RSA 安全性依賴于大型質數和復雜的操作。對于大多數計算系統來說,即使是通過其帶有大鑰匙的陷門功能的簡單路徑也很麻煩。因此,RSA 通常用作發送共享加密密鑰的工具,這些密鑰可用于更快的對稱算法,如 DES、3DES 和 AES,用于單個事務。
ECDSA 算法
橢圓曲線數字簽名算法 (ECDSA) 允許通信中的參與者通過基于稱為私鑰的隱藏信息為輸入消息生成數字簽名來證明真實性。此密鑰用于生成公鑰,其他人使用該公鑰來驗證參與者的真實性。
數字簽名是使用輸入消息、私鑰和隨機數生成的。然后,可以使用公鑰來驗證簽名者(或參與者)是否擁有相應的私鑰,因此是否真實。圖 9 說明了此概念。
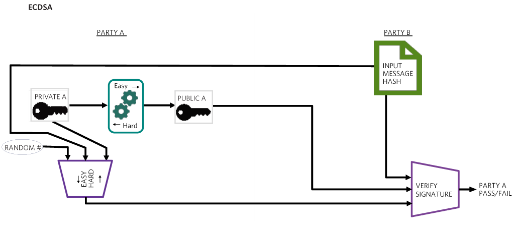
圖9.ECDSA(橢圓曲線數字簽名算法)有助于驗證數字簽名。
數字簽名算法最初是用模算術引入的,它依賴于大素數和需要大量使用計算能力的計算。橢圓曲線密碼學的引入利用橢圓函數的數學特性在不犧牲安全性的情況下簡化數學。
密鑰生成和簽名操作稱為單向或“陷門”函數。它們是橢圓曲線計算,在一個方向上計算相對簡單,但在另一個方向上計算起來卻很困難。私鑰可以被視為打開一個活板門,揭示了繞過試圖破壞密鑰生成或簽名操作的復雜迷宮的捷徑。
ECDSA 允許一方簽署來自任何一方的消息。但是,為了證明 ECDSA 的真實性,簽名者不得預先知道要簽名的消息。由于缺乏對消息的控制,通信中的另一個參與者可以用新信息“挑戰”簽名者,以證明擁有私鑰。
ECDH密鑰交換協議
橢圓曲線Diffie-Hellman(ECDH)密鑰交換允許雙方建立一個共享密鑰,以便僅與一條稱為私鑰的隱藏信息進行通信。如果沒有相關方之一的私鑰,竊聽者就無法輕松確定共享密鑰。但是,該算法允許將一方的私鑰和另一方的公鑰組合在一起,以生成對雙方都相同的結果密鑰。圖 10 說明了此概念。
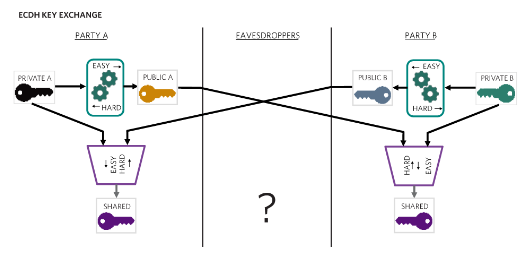
圖 10.ECDH密鑰交換允許雙方建立共享密鑰以進行通信。
ECDH密鑰交換
Diffie-Hellman密鑰交換首先是用模算術引入的,它依賴于大素數和需要大量使用計算能力的計算。橢圓曲線密碼學的引入利用橢圓函數的數學特性在不犧牲安全性的情況下簡化數學。
密鑰生成和組合密鑰操作稱為 1 路或“陷門”函數。它們是橢圓曲線計算,在一個方向上計算相對簡單,但在另一個方向上計算起來卻很困難。私鑰可以被視為打開一個活板門,揭示了繞過試圖破壞密鑰生成或組合操作的復雜迷宮的捷徑。
ECDH算法允許雙方一起建立密鑰,但它不能保證任何一方都是可信的。為此,需要額外的身份驗證層。例如,如果為公鑰提供了證書,例如使用來自受信任密鑰持有者的私鑰計算的 ECDSA(橢圓曲線數字簽名算法)簽名,則通過使用受信任持有者的公鑰對證書進行身份驗證來驗證公鑰的認證。
通過使用公鑰和來自受信任機構的證書,ECDH的參與者可以確定他們的對應方是真實的參與者。關注我們的密碼學教程系列中的其他部分,以繼續加深您對這種重要安全技術的理解。
審核編輯:郭婷
-
密鑰
+關注
關注
1文章
141瀏覽量
19851 -
函數
+關注
關注
3文章
4346瀏覽量
62969 -
XOR
+關注
關注
0文章
12瀏覽量
162028
發布評論請先 登錄
相關推薦
STM32密碼學訣竅,這套資料幫助你掌握!(方法論+加密庫資料合集)
物聯網安全機制密碼學基礎
java實現非對稱加密算法的過程
非對稱密鑰的應用有哪些
如何理解區塊鏈密碼學中的非對稱加密
橢圓曲線密碼學詳細解析
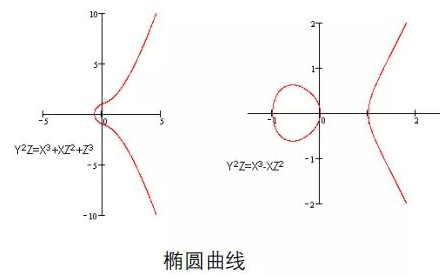




 密碼學:如何使用非對稱密鑰算法來交換共享私鑰
密碼學:如何使用非對稱密鑰算法來交換共享私鑰










評論