總的來說,對采樣率的討論就像看著油漆變干。我們真的需要深入了解細節嗎?畢竟,每個人都知道,您只需要以目標信號頻率的兩倍進行采樣即可獲得良好的結果,對吧?如果你對最后一句話的回答是“對!”,也許你應該繼續讀下去。雖然所謂的奈奎斯特速率(即最高信號頻率分量的兩倍)確實是消除混疊頻率所需的采樣速率,但該規則經常被忽視的限定符是,被數字化的信號必須被帶寬限制在等于奈奎斯特速率一半的值。重要的不僅僅是您感興趣的頻率,還有您數字化的信號中包含的所有頻率以及它們與您選擇的采樣率的比較情況。讓我們回到基礎。
什么是別名頻率?
韋伯斯特將“別名”定義為假名或附加名稱。出于數據采集的目的,我們可以更準確地將別名定義為假定頻率或附加頻率。
在觀看超速行駛的汽車的電影時,您看著汽車的車輪,它們似乎旋轉得不可思議,甚至向后旋轉。您看到的是由汽車車輪的快速旋轉速率與用于記錄圖像的相機的慢得多的幀速率之間的數學碰撞引起的混疊頻率。你下意識地從對圖像的解釋中過濾掉這種異常,因為從其他參考系中很容易確定汽車正在高速前進。但是,如果您正在觀看一部關于汽車車輪的電影呢?在這種情況下,如果被要求確定汽車移動的速度和方向,你可能會得出一個完全不同的、錯誤的和令人尷尬的結論。
擴展上面的例子,您可以將相機視為數據采集系統,將旋轉輪視為它正在數字化的信號。如果數據采集系統的采樣速率相對于信號頻率太慢,您的測量就會崩潰。你沒有電影的方便參考框架。您所擁有的只是隨時間變化的信號幅度的集合。哪些是真實的,哪些是別名?就像試圖通過只看車輪來解釋電影中汽車的運動一樣,這是不可能知道的,而且你的測量值有太多的東西無法猜測。
別名頻率的數學
如果我們知道輸入信號的頻率和采樣率,我們可以預測混疊頻率。公式(1)表明,混疊頻率是輸入信號頻率與采樣率的最接近整數倍之差絕對值的函數。

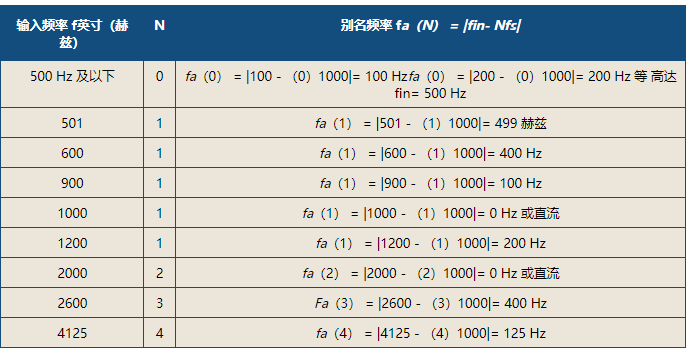
讓我們用一些例子來擴展這個等式。表1是以1000 Hz的固定速率采樣的各種正弦輸入信號頻率(fin)以及使用公式(1)計算得出的混疊頻率的匯編。常數 (N) 是一個整數,它假定使項 Nfs最接近輸入信號頻率 (fin) 所需的值。例如,如果輸入頻率為 150 Hz,采樣率為 75 Hz,則 N等于 2。如果輸入信號頻率增加到 188 Hz,N 將變為3,因為 75 和 3 (225) 的乘積比 75 和 2 (150) 的乘積更接近 188。
從表1可以看出,任何小于或等于500 Hz奈奎斯特值(采樣率的一半)的輸入信號頻率都會被準確再現。任何大于此值的頻率都會產生不準確的混疊頻率,甚至在輸入頻率是采樣速率的精確倍數時再現直流信號的程度也是如此。顯然,當輸入信號的頻率成分超過采樣率的一半時,所有的賭注都是錯誤的。
表 1:固定 1000 Hz 采樣率下的混疊與輸入頻率的關系
混疊頻率是什么樣的?這是陰險的事情。它看起來就像真實數據一樣。如果我們按照表(1)中所述的方式采集數據,當fin等于900 Hz時,我們會看到圖1所示的灰色100 Hz別名波形,而不是實際連接到數據采集系統的黑色900 Hz波形。除了較低的頻率,你能分辨出真實信號和鬼影之間的區別嗎?更復雜的是,我們大多數人不會四處奔波獲取純正弦波。典型的波形是許多頻率的復雜組合,而混疊的錄制波形可能看起來非常合理,但會導致您得出完全錯誤的結論。
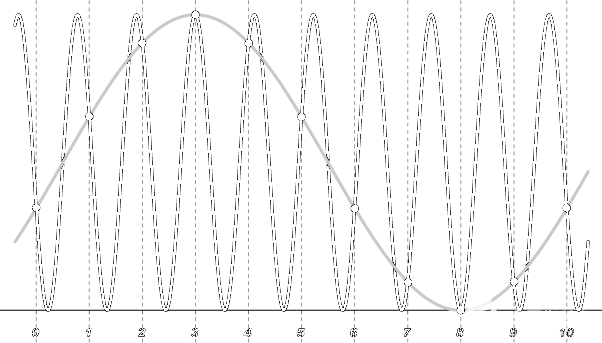
圖1 - 900 Hz波形(黑色)在1000 Hz采樣不足時產生混疊的100 Hz波形(灰色)
解決方案是什么?
回到本應用筆記開始的地方,只有確保信號中不存在高于此限值的其他頻率分量,我們才能滿足奈奎斯特采樣率準則,即目標最大信號頻率的兩倍。除非我們對信號源的頻率成分有高度的置信度,否則達到這一條件的唯一方法是在數字化之前將輸入信號應用于低通抗混疊濾波器。對抗混疊濾波器的深入討論超出了本應用筆記的范圍,但其顯著特性可歸納如下:
低通設計
選擇轉折頻率以達到您感興趣的最大頻率(即采樣率的一半)
從通帶到阻帶的陡峭過渡帶滾降。
圖2是上述理想抗混疊濾波器的圖形表示。請注意,在實際濾波器設計中,過渡帶的理想垂直形狀是不可能的,而是會產生帶有一些負斜率的滾降。這種現實迫使以較低的轉折頻率或較高的采樣率的形式進行折衷。例如,人耳可以響應高達 20 kHz 的頻率。如果可以使用符合理想的抗混疊濾波器,則可以使用40 kHz的采樣率對音樂進行數字化。然而,44.1 kHz的標準速率既反映了濾波器實現不理想的現實,也反映了保持20 kHz完整響應的愿望。
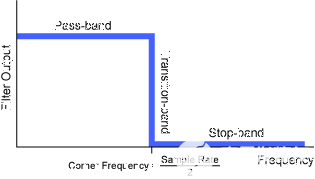
圖2 - 理想抗混疊濾波器的圖形表示。
您真的需要抗鋸齒過濾器嗎?
該領域的權威人士堅持認為,在沒有抗鋸齒濾波器的情況下獲取的數據是無用的。這些人可能會堅持讓你系安全帶只是為了把車開進車庫,因為“安全帶可以挽救生命”。事實上,在日常測量中采集的大部分數據不需要抗混疊濾波器來產生完全準確和可操作的結果,這就是為什么絕大多數數據采集和數據記錄儀儀器不會在每個測量通道中內置一個。任何不同意這種說法的人都應該問問自己是否需要濾波器來測量電池電壓 - 純 0 Hz。如果沒有,那么我們至少已經打開了妥協的大門,我們可以進一步打開它,包括其他直流或近直流信號的測量:溫度、濕度、直流電流、流量、壓力、負載、扭矩、頻譜圖、GSR、平滑和骨骼肌浴等。那么頻率成分被明確定義和包含的信號呢:50/60/400 Hz 電壓和電流、血壓和流量,甚至一些生物電位,如 ECG 和 EMG?我們開始覆蓋許多測量領域,而無需過濾器。還有更多的例子,但過濾器確實有其位置。
基于加速度計的測量是抗混疊濾波器幾乎需要的最佳示例。大多數壓電加速度計的頻率響應超過15 kHz。盡管您感興趣的頻率可能遠低于此頻率(例如,由于軸承磨損而導致的 40 Hz 電機隆隆聲),但您不能忽視傳感器可以并且將會通過更高頻率的事實。如果你已經讀到這里,你應該知道,僅僅因為你對40 Hz以上的頻率不感興趣并不意味著你只需要在80 Hz左右采樣,如果傳感器可以通過更高幾個數量級的頻率。
您可能需要過采樣
到目前為止,我們已經看到,帶寬受限的輸入信號以至少兩倍于抗混疊濾波器轉折頻率的速率采樣,可以再現輸入信號的頻率成分。如果您只對被測系統的頻率內容感興趣,并且有些應用是分析的范圍,那就太好了。回到加速度計的例子,你真的不在乎波形是什么樣子的,因為它是頻譜來傳達電機隆隆聲的存在和頻率。但是對于波形形狀確實傳達信息的其他應用,祝你好運,每個周期從兩個樣本中提取信息。參考圖1所示的100 Hz混疊波形,您甚至無法僅用兩個點遠程重建正弦波。每當您需要精確的波形再現時,您唯一的辦法就是以超過奈奎斯特最小值 2 倍(通常為 10 倍或更多)的速率進行過采樣。假設您已經準確地考慮了信號的頻率內容并消除了混疊頻率的可能性,則您選擇的實際倍數由個人喜好決定。
審核編輯:郭婷
-
濾波器
+關注
關注
161文章
7860瀏覽量
178932 -
數據采集
+關注
關注
39文章
6252瀏覽量
114045 -
采樣率
+關注
關注
0文章
77瀏覽量
16824
發布評論請先 登錄
相關推薦




 關于采樣率,您真正需要了解的內容
關于采樣率,您真正需要了解的內容












評論