本篇通過一道面試題,一個面試場景,來好好分析一下如何求遞歸算法的時間復雜度。
相信很多同學對遞歸算法的時間復雜度都很模糊,那么這篇Carl來給大家通透的講一講。
同一道題目,同樣使用遞歸算法,有的同學會寫出了O(n)的代碼,有的同學就寫出了O(logn)的代碼。
這是為什么呢?
如果對遞歸的時間復雜度理解的不夠深入的話,就會這樣!
那么我通過一道簡單的面試題,模擬面試的場景,來帶大家逐步分析遞歸算法的時間復雜度,最后找出最優解,來看看同樣是遞歸,怎么就寫成了O(n)的代碼。
面試題:求x的n次方
想一下這么簡單的一道題目,代碼應該如何寫呢。最直觀的方式應該就是,一個for循環求出結果,代碼如下:
intfunction1(intx,intn){
intresult=1;//注意任何數的0次方等于1
for(inti=0;ireturnresult;
}
時間復雜度為O(n),此時面試官會說,有沒有效率更好的算法呢。
如果此時沒有思路,不要說:我不會,我不知道了等等。
可以和面試官探討一下,詢問:“可不可以給點提示”。面試官提示:“考慮一下遞歸算法”。
那么就可以寫出了如下這樣的一個遞歸的算法,使用遞歸解決了這個問題。
intfunction2(intx,intn){
if(n==0){
return1;//return1同樣是因為0次方是等于1的
}
returnfunction2(x,n-1)*x;
}
面試官問:“那么這個代碼的時間復雜度是多少?”。
一些同學可能一看到遞歸就想到了O(logn),其實并不是這樣,遞歸算法的時間復雜度本質上是要看:遞歸的次數 * 每次遞歸中的操作次數。
那再來看代碼,這里遞歸了幾次呢?
每次n-1,遞歸了n次時間復雜度是O(n),每次進行了一個乘法操作,乘法操作的時間復雜度一個常數項O(1),所以這份代碼的時間復雜度是 n * 1 = O(n)。
這個時間復雜度就沒有達到面試官的預期。于是又寫出了如下的遞歸算法的代碼:
intfunction3(intx,intn){
if(n==0){
return1;
}
if(n%2==1){
returnfunction3(x,n/2)*function3(x,n/2)*x;
}
returnfunction3(x,n/2)*function3(x,n/2);
}
面試官看到后微微一笑,問:“這份代碼的時間復雜度又是多少呢?” 此刻有些同學可能要陷入了沉思了。
我們來分析一下,首先看遞歸了多少次呢,可以把遞歸抽象出一顆滿二叉樹。剛剛同學寫的這個算法,可以用一顆滿二叉樹來表示(為了方便表示,選擇n為偶數16),如圖:
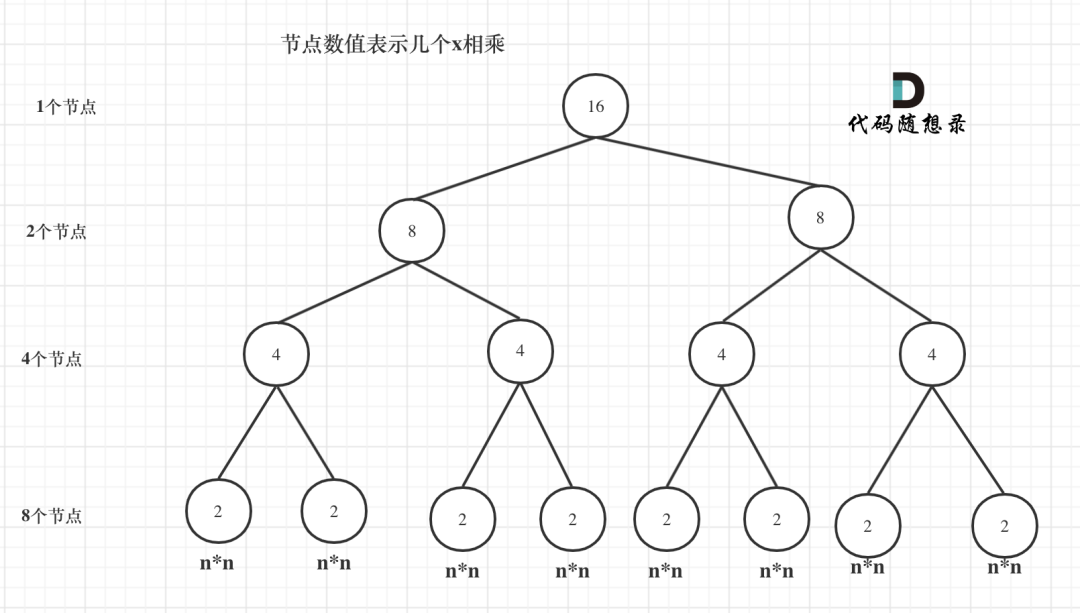
當前這顆二叉樹就是求x的n次方,n為16的情況,n為16的時候,進行了多少次乘法運算呢?
這棵樹上每一個節點就代表著一次遞歸并進行了一次相乘操作,所以進行了多少次遞歸的話,就是看這棵樹上有多少個節點。
熟悉二叉樹話應該知道如何求滿二叉樹節點數量,這顆滿二叉樹的節點數量就是2^3 + 2^2 + 2^1 + 2^0 = 15,可以發現:這其實是等比數列的求和公式,這個結論在二叉樹相關的面試題里也經常出現。
這么如果是求x的n次方,這個遞歸樹有多少個節點呢,如下圖所示:(m為深度,從0開始)
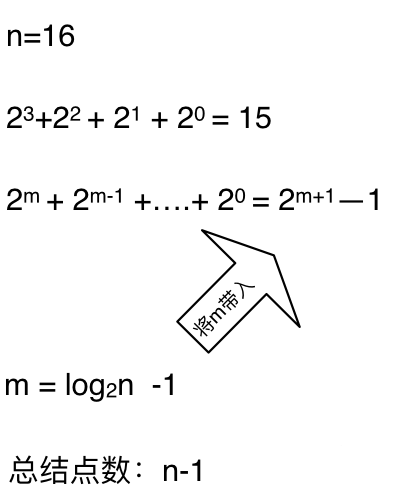
時間復雜度忽略掉常數項-1之后,這個遞歸算法的時間復雜度依然是O(n)。對,你沒看錯,依然是O(n)的時間復雜度!
此時面試官就會說:“這個遞歸的算法依然還是O(n)啊”, 很明顯沒有達到面試官的預期。
那么O(logn)的遞歸算法應該怎么寫呢?
想一想剛剛給出的那份遞歸算法的代碼,是不是有哪里比較冗余呢,其實有重復計算的部分。
于是又寫出如下遞歸算法的代碼:
intfunction4(intx,intn){
if(n==0){
return1;
}
intt=function4(x,n/2);//這里相對于function3,是把這個遞歸操作抽取出來
if(n%2==1){
returnt*t*x;
}
returnt*t;
}
再來看一下現在這份代碼時間復雜度是多少呢?
依然還是看他遞歸了多少次,可以看到這里僅僅有一個遞歸調用,且每次都是n/2 ,所以這里我們一共調用了log以2為底n的對數次。
每次遞歸了做都是一次乘法操作,這也是一個常數項的操作,那么這個遞歸算法的時間復雜度才是真正的O(logn)。
此時大家最后寫出了這樣的代碼并且將時間復雜度分析的非常清晰,相信面試官是比較滿意的。
總結
對于遞歸的時間復雜度,畢竟初學者有時候會迷糊,刷過很多題的老手依然迷糊。
本篇我用一道非常簡單的面試題目:求x的n次方,來逐步分析遞歸算法的時間復雜度,注意不要一看到遞歸就想到了O(logn)!
同樣使用遞歸,有的同學可以寫出O(logn)的代碼,有的同學還可以寫出O(n)的代碼。
對于function3 這樣的遞歸實現,很容易讓人感覺這是O(logn)的時間復雜度,其實這是O(n)的算法!
intfunction3(intx,intn){
if(n==0){
return1;
}
if(n%2==1){
returnfunction3(x,n/2)*function3(x,n/2)*x;
}
returnfunction3(x,n/2)*function3(x,n/2);
}
可以看出這道題目非常簡單,但是又很考究算法的功底,特別是對遞歸的理解,這也是我面試別人的時候用過的一道題,所以整個情景我才寫的如此逼真,哈哈。
大廠面試的時候最喜歡用“簡單題”來考察候選人的算法功底,注意這里的“簡單題”可并不一定真的簡單哦!
如果認真讀完本篇,相信大家對遞歸算法的有一個新的認識的,同一道題目,同樣是遞歸,效率可是不一樣的!
審核編輯 :李倩
-
算法
+關注
關注
23文章
4630瀏覽量
93352 -
代碼
+關注
關注
30文章
4825瀏覽量
69044 -
遞歸
+關注
關注
0文章
29瀏覽量
9070
發布評論請先 登錄
相關推薦
AI時代下芯片復雜度飆升,思爾芯國產硬件仿真加速芯片創新

芯片設計復雜度劇增,紫光芯片云 3.0 助力企業搭建專業設計環境

NPU與機器學習算法的關系
淺談Vivado編譯時間




 如何求遞歸算法的時間復雜度
如何求遞歸算法的時間復雜度











評論