
簡 介:利用FFT算法實(shí)現(xiàn)快速傅里葉變換, 在理論、工程中具有非常廣泛的應(yīng)用。除了能夠在合適的計(jì)算平臺(tái)完成FFT算法,同時(shí)還需要注意到它在頻譜分析中可能帶來的頻率混疊以及頻率泄露等問題。
今天下午的信號(hào)與系統(tǒng), 給同學(xué)們介紹了離散傅里葉變換的基本應(yīng)用, 并且介紹了快速傅里葉變換(FFT)的主要思想與算法。FFT算法因其優(yōu)異的性能和廣泛的應(yīng)用, 堪稱信息處理領(lǐng)域的原子武器。實(shí)現(xiàn)FFT編程語言很多, 比較來比較去, 利用Python語音所描述的該算法最為簡明和優(yōu)雅。
1.1 FFT算法代碼
下面的代碼是在 The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?視頻中給出的 FFT 遞歸算法形式, 最大精度反映了FFT算法核心。
這個(gè)代碼實(shí)現(xiàn)了DIF(時(shí)域抽取快速傅里葉變換), 利用遞歸定義,將FFT核心算法中的分而治之體現(xiàn)的淋漓盡致, 突出了遞歸核心中的核心思想。
defFFT(P):
n=len(P)
ifn*1:returnP
ye=FFT(P[0::2])
yo=FFT(P[1::2])
y=[0]*n
w=exp(-1j*2*pi/n)
forjinrange(n//2):
yow=w**j*array(yo)
y[j]=ye[j]+yow[j]
y[j+n//2]=ye[j]-yow[j]
returny
利用Python語音中對(duì)于數(shù)組切片操作語法, 還可以將上面FFT算法中的循環(huán)部分都替換成關(guān)于數(shù)組的操作, 使得實(shí)際運(yùn)算速度得到提高。
defFFT1(P):
n=len(P)
ifn*1:returnP
ye=FFT(P[0::2])
yo=FFT(P[1::2])
w=exp(-1j*2*pi/n)**array(list(range(n//2)))
yow=w*yo
y=[0]*n
y[:n//2]=ye+yow
y[n//2:]=ye-yow
returny
1.2 FFT 算法測(cè)試
為了測(cè)試算法的有效性, 下面對(duì)于一個(gè)方波信號(hào)計(jì)算對(duì)應(yīng)的FFT結(jié)果。
測(cè)試算法代碼如下:
LEN=1024
oneLEN=10
p1=[1]*oneLEN+[0]*(LEN-oneLEN)
y=FFT(p1)
plt.plot(abs(array(y)),label='abs(FFT)')
plt.plot(p1,label='Data')
plt.xlabel("y")
plt.ylabel("abs(FFT(y))")
plt.grid(True)
plt.legend(loc='upperright')
plt.tight_layout()
plt.show()
下面是測(cè)試?yán)肞ython語言實(shí)現(xiàn)的FFT算法計(jì)算結(jié)果。
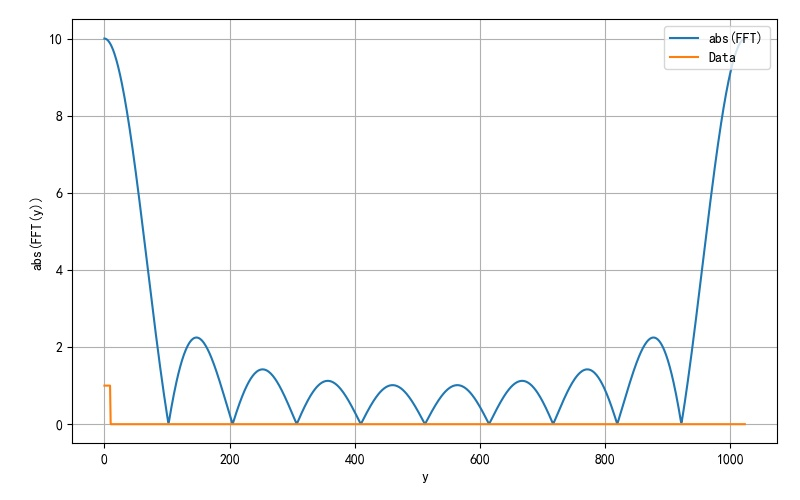 ▲ 圖1.2.1 利用Python語音實(shí)現(xiàn)的FFT算法測(cè)試結(jié)果
▲ 圖1.2.1 利用Python語音實(shí)現(xiàn)的FFT算法測(cè)試結(jié)果FFT算法貴在計(jì)算效率,前面使用Python實(shí)現(xiàn)FFT,雖然形式上優(yōu)雅,但實(shí)際執(zhí)行效率不高。提高執(zhí)行效率,還是需要使用編譯語言。
2.1 Fortran FFT算法
在我上大學(xué)期間所學(xué)的編程語言為Fortran, 估計(jì)現(xiàn)在沒有多少同學(xué)學(xué)習(xí)這個(gè)算法語言。下面給出了利用Fortran語言實(shí)現(xiàn)的FFT算法程序。
算法整體上包括有兩個(gè)階段:
- 第一個(gè)階段實(shí)現(xiàn)了對(duì)輸入數(shù)據(jù)進(jìn)行倒讀順序排列;
- 第二階段利用三重循環(huán)實(shí)現(xiàn)了分組蝶形運(yùn)算。
當(dāng)然了,時(shí)過三十年再看Fortran感覺十分酸爽, 但它簡練語言和執(zhí)行高效還是讓我們回憶起當(dāng)年編程時(shí)所感覺到的快樂。
 ▲ 圖 Fortran 語言實(shí)現(xiàn)的FFT算法
▲ 圖 Fortran 語言實(shí)現(xiàn)的FFT算法2.2 C語言FFT算法
下面是在網(wǎng)絡(luò)上博文C++ Program to Compute Discrete Fourier Transform using Fast Fourier Transform Approach[1]給出的FFT算法, 沒有對(duì)其功能進(jìn)行測(cè)試。相比于前面利用Python,F(xiàn)ortran來看, C語言實(shí)現(xiàn)FFT就顯得非常啰嗦了。
#include
利用FFT算法實(shí)現(xiàn)快速傅里葉變換, 在理論、工程中具有非常廣泛的應(yīng)用。除了能夠在合適的計(jì)算平臺(tái)完成FFT算法,同時(shí)還需要注意到它在頻譜分析中可能帶來的頻率混疊以及頻率泄露等問題。
審核編輯:湯梓紅-
算法
+關(guān)注
關(guān)注
23文章
4630瀏覽量
93351 -
FFT
+關(guān)注
關(guān)注
15文章
437瀏覽量
59561 -
python
+關(guān)注
關(guān)注
56文章
4807瀏覽量
85037 -
傅里葉變換
+關(guān)注
關(guān)注
6文章
442瀏覽量
42708
原文標(biāo)題:優(yōu)雅的FFT算法
文章出處:【微信號(hào):FANYPCB,微信公眾號(hào):凡億PCB】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
Vivado中快速傅里葉變換FFT IP的配置及應(yīng)用
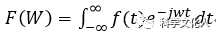
快速傅里葉變換C語言實(shí)現(xiàn)
詳解快速傅里葉變換FFT算法
快速傅里葉變換FFT的C程序代碼實(shí)現(xiàn)




 利用FFT算法實(shí)現(xiàn)快速傅里葉變換
利用FFT算法實(shí)現(xiàn)快速傅里葉變換










評(píng)論