啊，我終于可以寫文章了！最近兩天好累哇，先繼續寫上面的算法文章。

這篇文章寫的算法是高斯消元，是數值計算里面基本且有效的算法之一：是求解線性方程組的算法。

這里再細寫一下：

在數學中，高斯消元法，也稱為行約簡，是一種求解線性方程組的算法。它由對相應的系數矩陣執行的一系列操作組成。此方法還可用于計算矩陣的秩、方陣的行列式和可逆矩陣的逆矩陣。該方法以卡爾·弗里德里希·高斯 ( Carl Friedrich Gauss ，1777-1855)的名字命名，盡管該方法的一些特例——盡管沒有證明——早在公元 179 年左右就為中國數學家所知。

為了對矩陣執行行縮減，可以使用一系列基本行操作來修改矩陣，直到矩陣的左下角盡可能地用零填充。基本行操作分為三種類型：

1.交換兩行，

2.將一行乘以一個非零數，

3.將一行的倍數添加到另一行。（減法可以通過將一行乘以 -1 并將結果添加到另一行來實現）

使用這些操作，矩陣總是可以轉換為上三角矩陣，實際上是行梯形矩陣。一旦所有前導系數（每行中最左邊的非零條目）都為 1，并且包含前導系數的每一列在其他地方都為零，則稱該矩陣為簡化行梯形形式。這種最終形式是獨一無二的；換句話說，它與所使用的行操作序列無關。例如，在下面的行操作序列中（在第一步和第三步對不同行進行兩個基本操作），第三和第四個矩陣是行梯形矩陣，最后一個矩陣是唯一的簡化行梯隊形式。

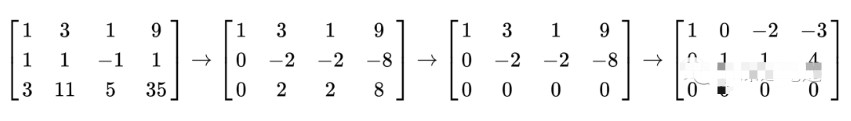
一個矩陣的簡化

使用行操作將矩陣轉換為簡化的行梯形形式有時稱為Gauss-Jordan 消元法。在這種情況下，術語高斯消元是指過程，直到它達到其上三角形或（未簡化的）行梯形形式。出于計算原因，在求解線性方程組時，有時最好在矩陣完全約簡之前停止行操作。

我們對其實現的操作只有這三個

如果矩陣與線性方程組相關聯，則這些操作不會更改解集。因此，如果一個人的目標是求解線性方程組，那么使用這些行操作可以使問題變得更容易。

對于矩陣中的每一行，如果該行不只包含零，則最左邊的非零條目稱為該行的前導系數（或樞軸）。因此，如果兩個前導系數在同一列中，則可以使用類型 3的行操作使這些系數之一為零。然后通過使用行交換操作，總是可以對行進行排序，以便對于每個非零行，前導系數位于上一行的前導系數的右側。如果是這種情況，則稱矩陣為行梯形. 所以矩陣的左下部分只包含零，并且所有的零行都在非零行的下方。這里使用“梯隊”一詞是因為可以粗略地認為行是按大小排列的，最大的位于頂部，最小的位于底部。

例如，下面的矩陣是行梯形的，它的前導系數用紅色表示：

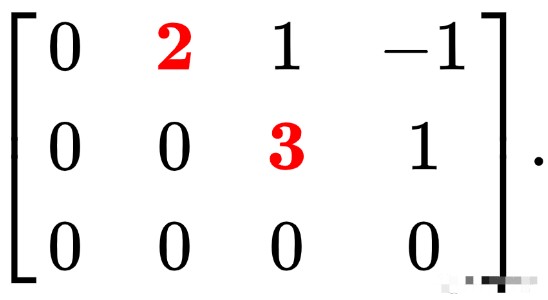
就像這樣

它是梯形的，因為零行在底部，第二行（第三列）的領先系數在第一行（第二列）的領先系數的右側。

如果矩陣的所有前導系數都等于 1（這可以通過使用類型 2 的基本行操作來實現），并且在包含前導系數的每一列中，則稱矩陣為簡化行梯形。該列中的其他條目為零（可以通過使用類型 3 的基本行操作來實現）。

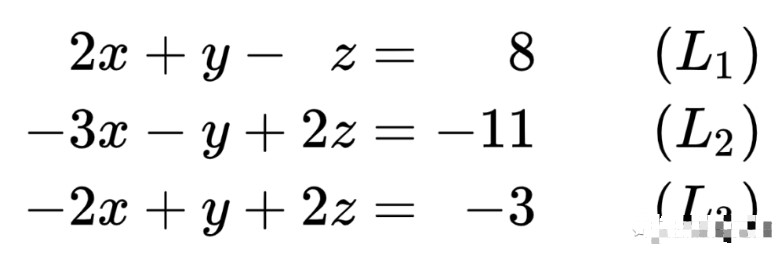
假如我們求解這個方程的解

下表是同時應用于方程組及其相關增廣矩陣的行縮減過程。在實踐中，通常不會用方程來處理系統，而是使用更適合計算機操作的增廣矩陣。行縮減過程可以概括如下：從L1以下的所有方程中消除x，然后從L2以下的所有方程中消除y。這將使系統變成三角形。然后，使用反向替換，可以解決每個未知數。

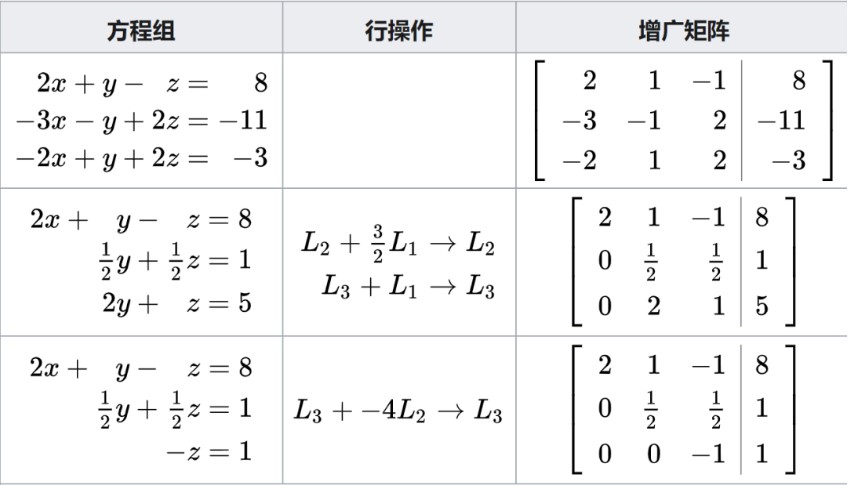
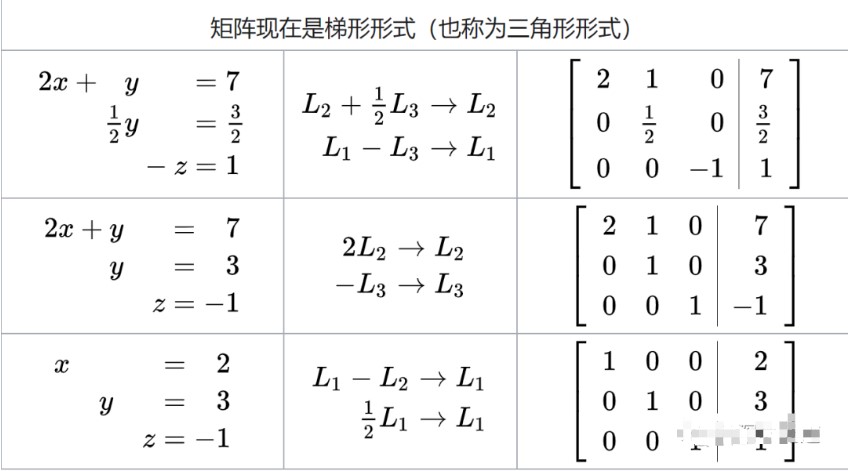
就好像這樣

其實還有內容，但是公式編輯實在不會哇，這里給出程序的偽代碼：

高斯消元法將給定的m × n矩陣A轉換為行梯形矩陣。

在下面的偽代碼中，A[i, j]表示矩陣A在第i行和第j列中的條目，索引從 1 開始。轉換在原地執行，這意味著原始矩陣丟失，最終被其行梯形形式替換。

看不懂？沒有關系，大致懂就行

程序的實現上面，我們導入這些內容

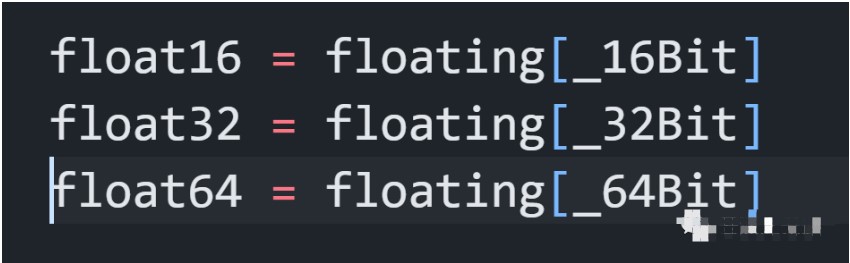
為了精度，導入float64

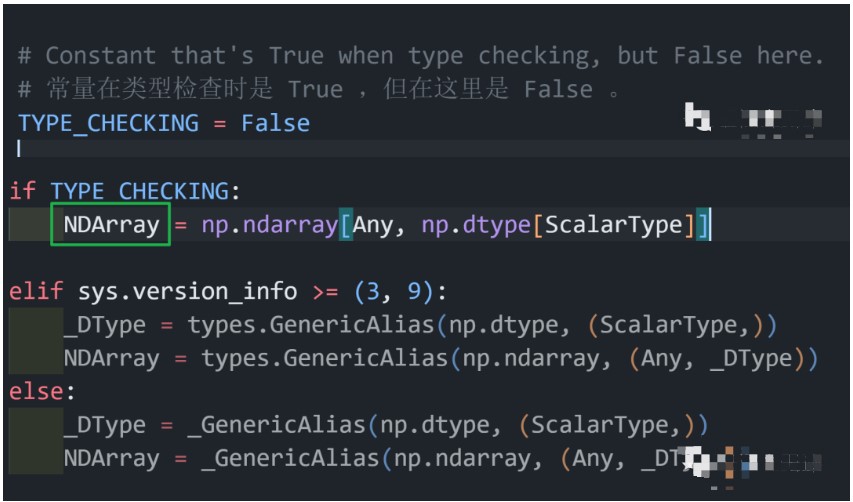
以及導入的一個N維的數組，在內部是所以ndarray封裝的

這樣學習的態度是不對的，我們需要看看Numpy文檔寫的：

64位精度浮點數類型：符號位、11位指數、52位尾數。

沒關系，你不懂的官網文檔滿足你

NDarray在這里

可在運行時用于鍵入具有給定 dtype 和未指定形狀的數組。

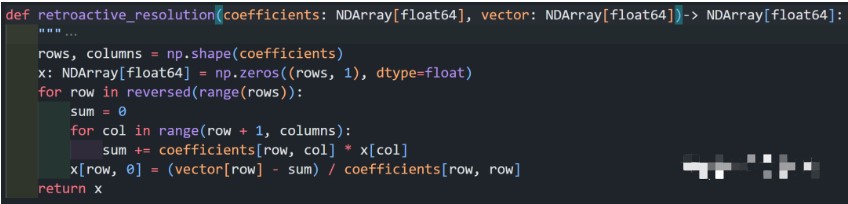
系數矩陣，向量是輸入的參數，后面是返回的數據類型。

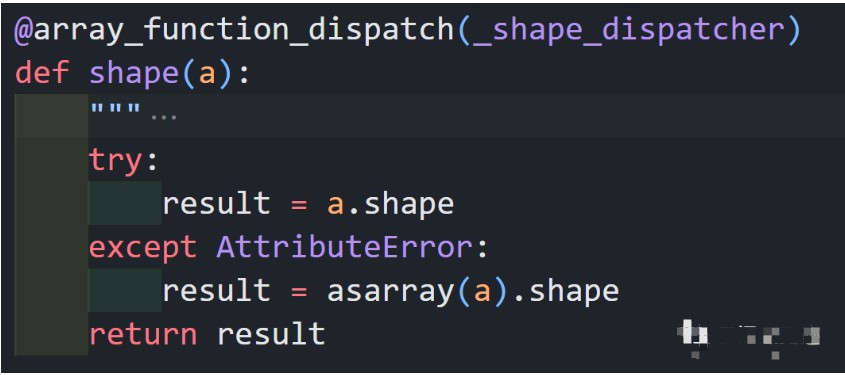
對shape函數感興趣不，內部是這樣的

這個也是注解的寫法，意思是返回一個數組，用0填充：

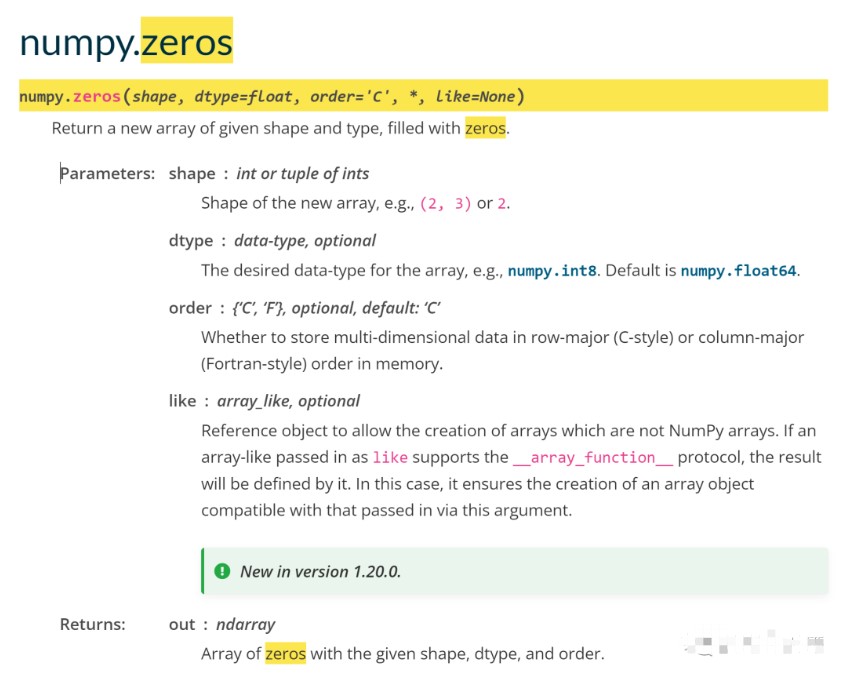
zeros函數的樣子

第一個參數，元組，說明樣子。后面參數是類型，這里寫float。返回值是具有給定形狀、數據類型和順序的零數組。

首先，reversed 函數返回一個反轉的迭代器。這個為什么倒著算呢？是因為倒著算對算法來講有一些優點。

內部再套一個函數，內部對列處理，下面的代碼就是實現使用倍數的關系對一整行處理，[]是相當于數組的index寫法，下面是將處理結果應用到行，最后打印X。

上面這個函數是高斯函數的一個子函數，作用是給出最簡的階梯行列式。

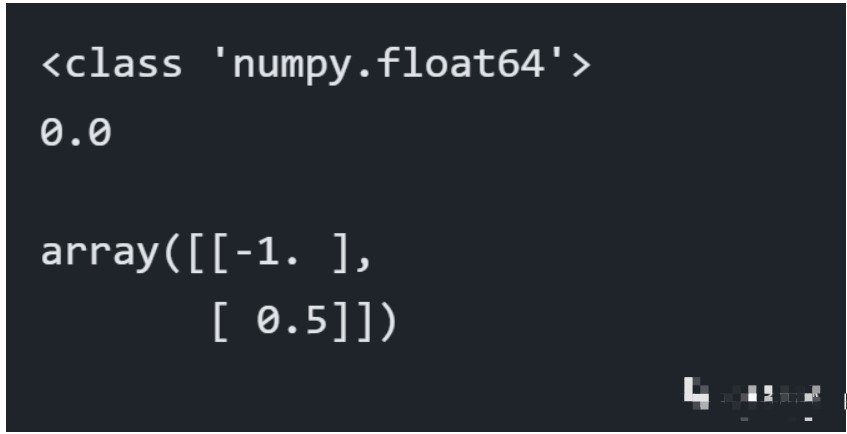
我們要算這個

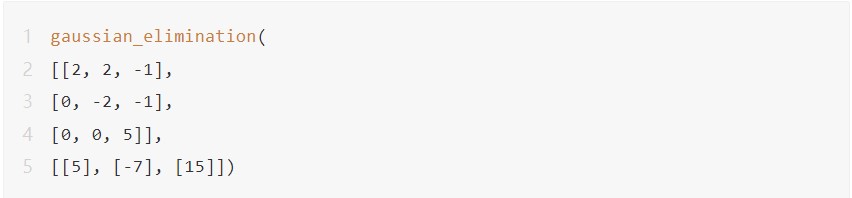
輸入的時候這樣輸入，先別繼續看，我們看高斯分解

這個檢查寫的很簡單

接下來

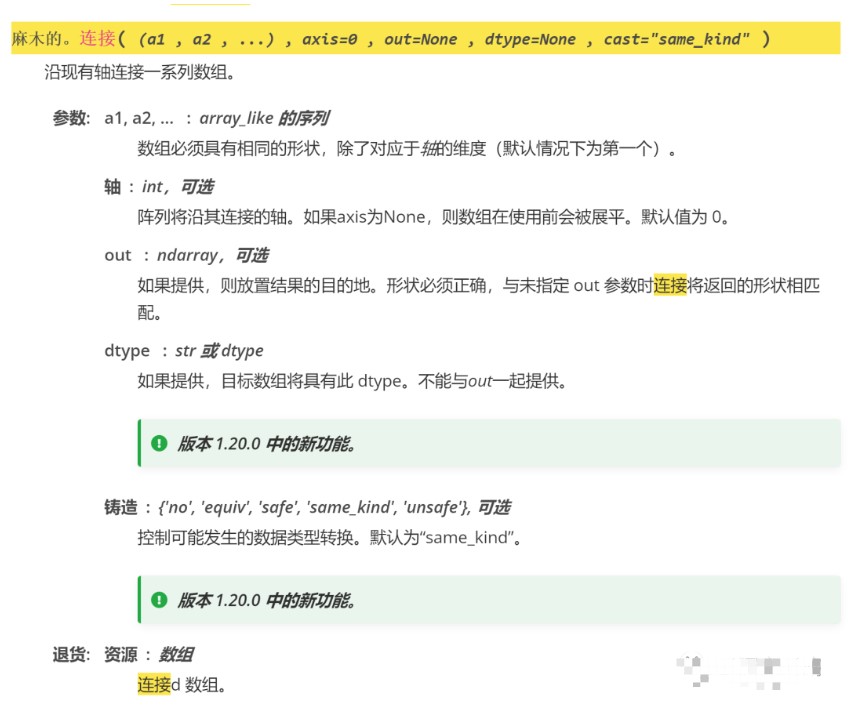
連接我們的矩陣，要求有相應的形狀

這個例子不錯

0是按照行展開，1是列，None是直接接龍。

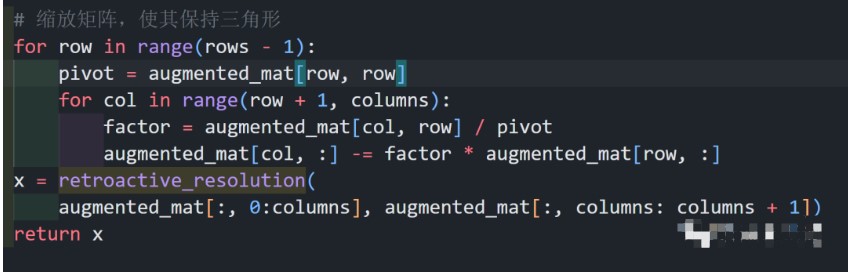
這段實現的是上面的偽代碼

一個很有趣的變量名

調用的時候就是這樣，輸入一個大元組，里面有兩個小元組

審核編輯：劉清