文章來(lái)源：中科院物理所

原文作者：Kasper Müller

海森堡

我經(jīng)常聽到人們講，是因?yàn)橛^察者通過(guò)光子和電子發(fā)生相互作用使光子的動(dòng)量受到了影響，所以才導(dǎo)致了海森堡不確定性原理。

觀察者必須通過(guò)影響電子的動(dòng)量（或一些量子態(tài)）來(lái)觀察它，這或許是真的，但這不是導(dǎo)致不確定性原理的真正原因！

在開始討論這個(gè)話題之前，讓我們先定義海森堡不確定性原理(Heisenberg’s uncertainty principle)。

在量子力學(xué)中，存在一系列關(guān)于共軛物理量（如位置和動(dòng)量）的不等式，它們限制了同時(shí)測(cè)量這些成對(duì)物理量的精度，這些不等式中的任意一個(gè)都可以被稱為不確定性原理（或是海森堡不確定性原理）。

-維基百科

一種常見的表述方式是，在任何給定的時(shí)間點(diǎn)，你都無(wú)法同時(shí)準(zhǔn)確地測(cè)量粒子的動(dòng)量和位置。

這種不確定性不取決于設(shè)備的好壞，也不是因?yàn)楹茈y消除測(cè)量誤差。無(wú)論我們做得多好，我們都無(wú)法同時(shí)精確測(cè)量這兩個(gè)量（如動(dòng)量和能量）…

首先，存在許多種不確定性原理，其中不少能在宏觀世界中看到。即使你沒有意識(shí)到它們的存在，但其實(shí)也一直在和這些現(xiàn)象打交道。

其次，海森堡不確定性原理背后與數(shù)學(xué)有著密切的關(guān)系。

所有波和物質(zhì)（共軛變量）都必須遵從一系列的不確定性原理，真正導(dǎo)出這些原理的是一個(gè)數(shù)學(xué)事實(shí)（稍后詳述）。

音樂(lè)、雷達(dá)技術(shù)、能源技術(shù)和光也有必須遵守的“不確定性原理”，我們很快就會(huì)看到，是數(shù)學(xué)決定了這一切。

波

一切都可以歸結(jié)為非常簡(jiǎn)單的事情。無(wú)論多復(fù)雜的的信號(hào)或函數(shù)，實(shí)際上都是正弦波的疊加。正弦波是具有特定波長(zhǎng)和振幅的波。

疊加僅僅意味著所有的波相互作用，所有波的和（稱為干涉）就是構(gòu)成更復(fù)雜信號(hào)的疊加。

也就是說(shuō)，我們可以將一個(gè)函數(shù)分解為組成它的更簡(jiǎn)單的部分（正弦波）。這幾乎就是我們?cè)谟?jì)算傅里葉級(jí)數(shù)的傅里葉系數(shù)時(shí)所要做的一切。值得的一提的是，這個(gè)方法對(duì)于非周期函數(shù)同樣適用。

這種效果在音樂(lè)中是眾所周知的，例如，吉他生中的泛音會(huì)干擾主波（弦的頻率）。也就是說(shuō)，吉他的聲音（以及任何其他樂(lè)器，包括你的聲音）是由頻率和振幅不同的正弦波組成的。

當(dāng)我們描述這樣一個(gè)復(fù)雜的信號(hào)時(shí)，我們有兩種等價(jià)的方式可以選擇。也就是說(shuō)，我們可以選擇兩種不同的單位對(duì)它進(jìn)行描述。

我們可以選擇用時(shí)間來(lái)描述產(chǎn)生干涉圖樣的所有波是如何同時(shí)相互作用的，也可以選擇用構(gòu)成干涉圖樣的正弦波的頻率來(lái)描述它。

可以用兩種等效的方式來(lái)描述的事件被稱為雙重關(guān)系（dual relationship）。

如果我們可以找到一個(gè)數(shù)學(xué)工具來(lái)描述時(shí)間信號(hào)和頻率信號(hào)之間的雙重關(guān)系，那當(dāng)然再好不過(guò)。事實(shí)上，我們確實(shí)找到了這樣的工具。

傅里葉變換

我上面提到的描述這種雙重關(guān)系的工具叫做傅里葉變換(Fourier transform)。毫無(wú)疑問(wèn)，它是數(shù)學(xué)工具中最強(qiáng)大、最常用的工具之一。

在給出它的一些特性之前，我們先講一講這種傅里葉變換的一些一般性質(zhì)：

傅里葉變換是一種積分變換（也就是一個(gè)算符），它拿到一個(gè)函數(shù)并返回另一個(gè)函數(shù)。

作為函數(shù)空間上的一個(gè)算符，我們可以把它看作是純數(shù)學(xué)的客體，但我們可以賦予它很好的物理解釋。在物理和數(shù)學(xué)領(lǐng)域，我們都可以使用它。

今天，我們主要將從物理學(xué)的角度來(lái)考慮它。

在下面的討論中，我們假設(shè)積分始終收斂。

令是一個(gè)可積函數(shù)。f的傅里葉變換由以下積分給出：

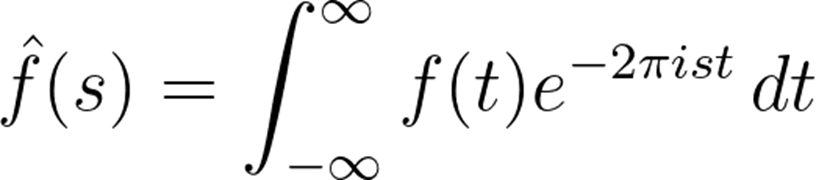
如果表示聲波隨時(shí)間的變化，那么傅里葉變換的結(jié)果表示構(gòu)成聲波的頻率，因此也可以看做是頻率的函數(shù)。

下面的動(dòng)圖顯示了聲波（圖中是單位脈沖信號(hào)）是如何由許多正弦波組成的，正弦波的疊加產(chǎn)生了函數(shù)，即。

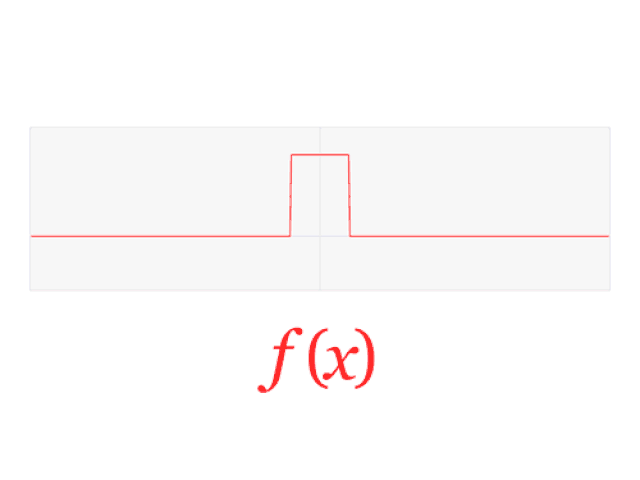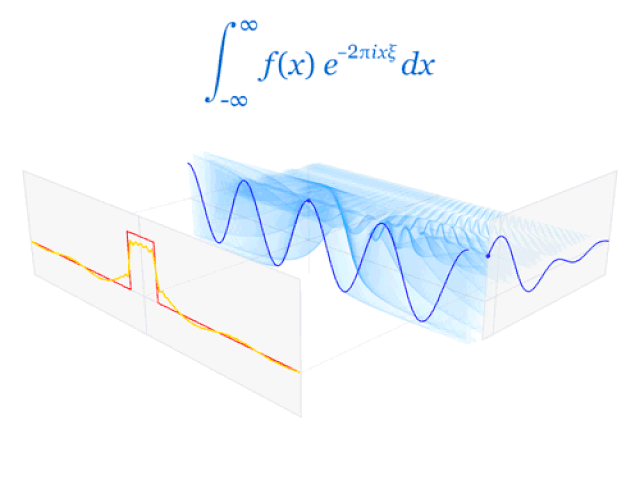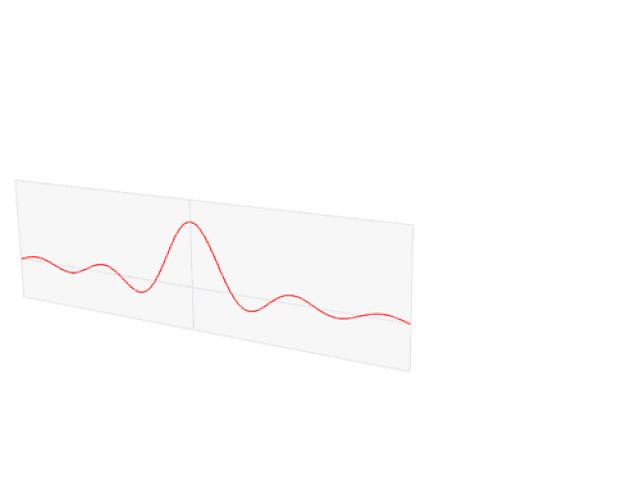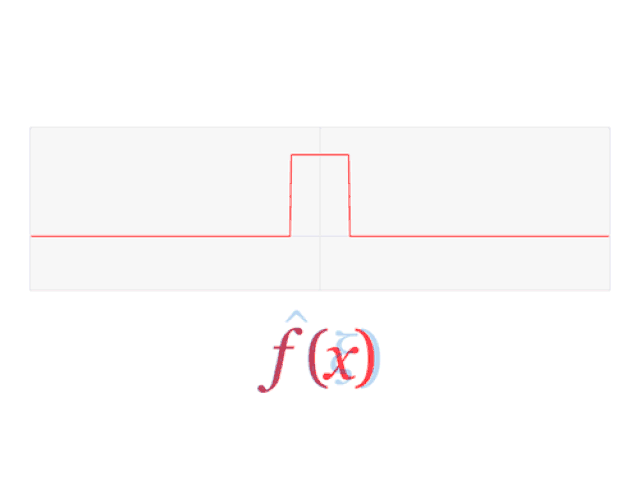
一個(gè)脈沖信號(hào)的傅里葉變換是一個(gè)sinc函數(shù)。所有信號(hào)都可以用時(shí)間或頻率表示的正弦波來(lái)構(gòu)造 來(lái)源：Lucas Vieira

理解信號(hào)總是可以用兩種等效的表達(dá)方式是非常重要的。只要給定其中一個(gè)，另一個(gè)是唯一確定的，我們有一個(gè)公式可以對(duì)它們進(jìn)行計(jì)算。如何選擇僅僅取決于我們想用什么方式表達(dá)一個(gè)信號(hào)。

唯一的傅立葉逆變換由以下公式得出：

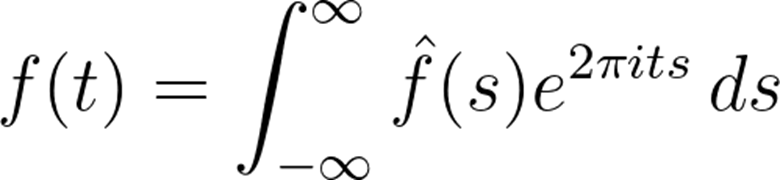
傅里葉變換的性質(zhì)

傅里葉變換不是一兩節(jié)課就可以講清楚的，我們只能在本文中講點(diǎn)皮毛。然而，傅里葉變換的一些令人驚奇的特性是一定要講的：

首先是平移的影響。假設(shè)。通過(guò)變量的變換，我們得到：

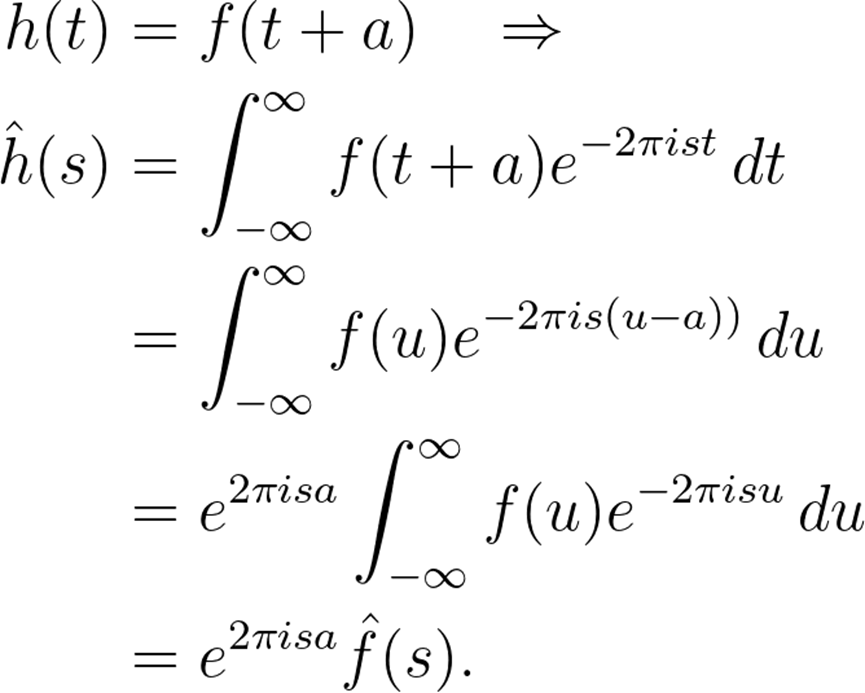
時(shí)間平移（信號(hào)延遲）會(huì)讓頻率函數(shù)產(chǎn)生一個(gè)相位移動(dòng)。那變量的縮放會(huì)產(chǎn)生什么影響呢？

假設(shè)。我們將分別從a<0和a>0進(jìn)行討論。

其中使用了代換u=at。讓我們看看當(dāng)a<0時(shí)會(huì)發(fā)生什么：

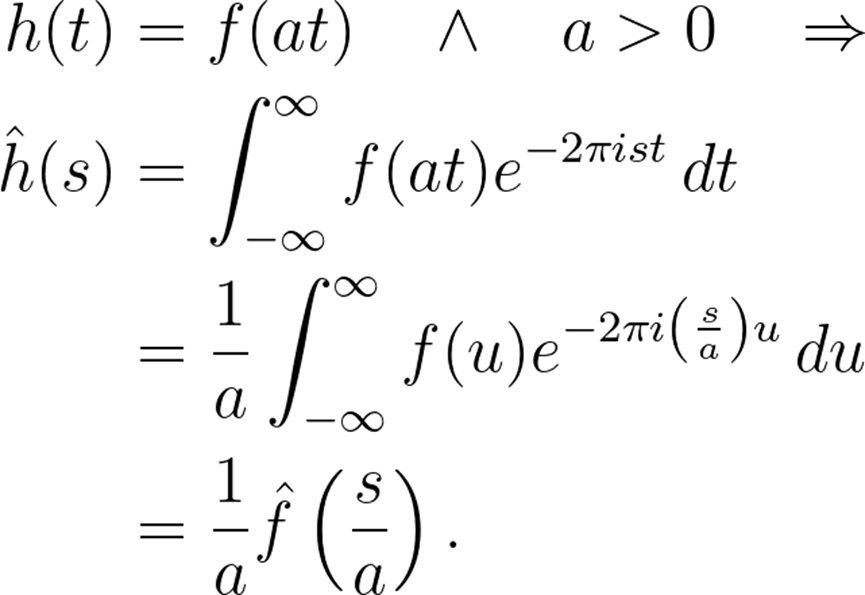
進(jìn)一步我們得到表達(dá)式：

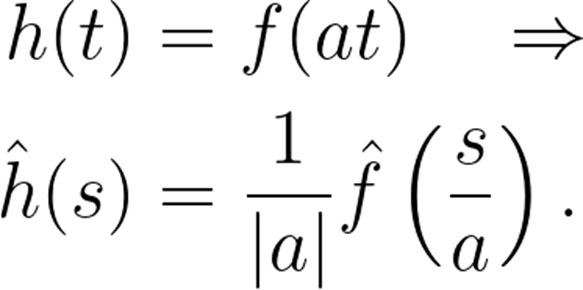
它的物理意義是什么？

傅里葉變換的標(biāo)度特性意味著，如果我們?cè)跁r(shí)間上壓縮信號(hào)，相當(dāng)于在頻率空間（水平）上擴(kuò)展信號(hào)，反之亦然。

我們很快就會(huì)發(fā)現(xiàn)，這一結(jié)果極其重要。

通過(guò)維度進(jìn)行分析可以給我們提供一個(gè)更高層次和有啟發(fā)性的視角。時(shí)間以秒為單位衡量，頻率以1/s為單位進(jìn)行衡量。似乎可以看出，如果把時(shí)間展寬變大，頻率展寬就會(huì)變小，反之亦然。

如果你不知道頻率的單位是從哪里來(lái)的，我非常能理解你的疑惑。傅里葉變換中的s最終決定了構(gòu)成信號(hào)的正弦波的周期，你可以通過(guò)使用歐拉公式將復(fù)指數(shù)展開為正弦和余弦，或者將傅里葉變換視為一組連續(xù)的傅里葉系數(shù)來(lái)感受這一點(diǎn)。

傅里葉變換有很多炫酷的特性，但由于這不僅僅是一篇關(guān)于變換本身的文章，我們將不過(guò)多介紹這些特性，感興趣的讀者可以自己來(lái)探索這一點(diǎn)。

讀者可能會(huì)發(fā)現(xiàn)一個(gè)讓計(jì)算變簡(jiǎn)便的特性，即傅里葉變換將求導(dǎo)數(shù)轉(zhuǎn)換為乘以一個(gè)常數(shù)，這是一個(gè)有趣且具有實(shí)用價(jià)值的特性。這意味著一個(gè)空間中的微分方程對(duì)應(yīng)于另一個(gè)空間中的代數(shù)方程。

因此，一些微分方程可以通過(guò)變換方程，用代數(shù)方法求解，然后將解變換回來(lái)（通過(guò)傅立葉逆變換）獲得原本方程的解。

波函數(shù)和海森堡不確定性原理

量子物理學(xué)家通過(guò)可能存在的量子態(tài)來(lái)描述量子系統(tǒng)（例如粒子）。

描述量子態(tài)的函數(shù)族被稱為波函數(shù)，以位置坐標(biāo)為變量的波函數(shù)的模平方給出了粒子在空間中的概率分布。

因此，我們可以將波函數(shù)解釋為概率波，表示粒子位于給定空間區(qū)域的概率。因此，描述粒子位置的波函數(shù)應(yīng)該被看作是空間中的波而不是時(shí)間中的波。

當(dāng)我們對(duì)這個(gè)位置波（位置坐標(biāo)為自變量的波函數(shù)）進(jìn)行傅里葉變換時(shí)，可以得到一個(gè)頻率（空間中的頻率）波，它是以粒子動(dòng)量為自變量的波函數(shù)。

仔細(xì)想想并不奇怪，因?yàn)槿绻阏J(rèn)為光是波包或物質(zhì)波，那么動(dòng)量將由光的頻率給出。

我們用和來(lái)表示這種關(guān)系。其中γ是波長(zhǎng)，h是普朗克常數(shù)，p是動(dòng)量，f是頻率，E是能量。

我們把一個(gè)粒子限制在越小的間隔內(nèi)，位置波函數(shù)就越局域化（被水平擠壓）。由于動(dòng)量波函數(shù)是位置波函數(shù)的傅里葉變換，動(dòng)量波函數(shù)將被水平拉伸，這意味著動(dòng)量將有更大的不確定性。這是之前提到的傅里葉變換的標(biāo)度特性導(dǎo)致的。

事實(shí)上，這就是海森堡的不確定性原理！這里只有傅里葉變換起了作用：

其中是普朗克常數(shù)，Δx和Δp分別是位置和動(dòng)量的不確定性（標(biāo)準(zhǔn)差）。

普遍的不確定性

當(dāng)函數(shù)是函數(shù)的傅里葉變換時(shí)，我們稱和為共軛變量或共軛對(duì)。事實(shí)上，對(duì)于任何共軛函數(shù)對(duì)，都存在不確定性原理。

海森堡不確定性原理只是共軛變量的特例。

從數(shù)學(xué)角度來(lái)看，為什么共軛變量的不確定性原理成立？原因是：短信號(hào)，如聲音脈沖，需要許多頻率不同的正弦波的疊加才能實(shí)現(xiàn)，只有許多特定頻率的正弦波的疊加才能保證在一定范圍之外波的振幅接近于0。相反，信號(hào)越像正弦波，描述信號(hào)所需的頻率就越少。

當(dāng)你聽到很短的一段聲音時(shí)，你很難確定這段聲音包含哪些頻率；但如果你聽到一段持續(xù)時(shí)間很長(zhǎng)的純凈信號(hào)，就能夠區(qū)分出不同的頻率。這也是不確定性原理。

同樣的，我們對(duì)雷達(dá)探測(cè)的目標(biāo)的距離知道得越多，對(duì)接近或后退的速度就知道得越少，反之亦然。這是多普勒和距離的不確定性。

還有其它許多共軛變量，它們都遵循各自的不確定性原理，它們有一個(gè)共同點(diǎn)，那就是它們的成立都是有數(shù)學(xué)保證的！波的數(shù)學(xué)只是限制了我們可以從某一量子態(tài)中獲取多少信息。

海森堡不確定性原理的影響真實(shí)存在

如果你把激光器對(duì)準(zhǔn)狹縫，光屏?xí)巡糠止庾钃踉谕猓瑢?duì)于穿透過(guò)去的一部分，接下來(lái)會(huì)發(fā)生神奇的事情。

光線似乎在狹縫后面的屏上擴(kuò)散開來(lái)，如果你讓狹縫變得更窄，那么光會(huì)彌散地更開。這似乎和我們的直覺不一致？我們限制它的空間分布，它反而彌漫開來(lái)。

這個(gè)現(xiàn)象就是由海森堡不確定性原理導(dǎo)致的。隨著狹縫越來(lái)越窄，位置波（波函數(shù)）越來(lái)越局域化（窄），根據(jù)不確定性原理，動(dòng)量波函數(shù)的展寬越來(lái)越大，這使得越來(lái)越多方向的運(yùn)動(dòng)成為可能。

由于動(dòng)量是一個(gè)有方向的矢量，這意味著光子在狹縫另一側(cè)傳播時(shí)彌散的角度變得越來(lái)越大，從而在屏上產(chǎn)生了美麗的衍射圖樣。

來(lái)源

不確定性還可以解釋為什么太陽(yáng)會(huì)發(fā)光，甚至可以解釋為什么霍金輻射的時(shí)空現(xiàn)象會(huì)讓黑洞縮小。

我希望有一點(diǎn)明確：不確定性是一種純粹的數(shù)學(xué)現(xiàn)象，但由于量子系統(tǒng)讓這些數(shù)學(xué)理論照進(jìn)現(xiàn)實(shí)，因此不確定性也可以被看成一種物理原理。

作者：Kasper Müller

翻譯：Nothing

審校：zhenni

原文鏈接：

https://www.cantorsparadise.com/heisenbergs-uncertainty-principle-is-pure-mathematics-e14c840659e1

編輯：黃飛