大家好,我是梁唐。
最近在劍指offer里看到一道算法題很有意思,分享給大家。
題面很簡單,只有一句話,叫做對一維數組做maxpooling。
可能很多同學不知道pooling是什么意思,pooling是深度學習中的一個術語,翻譯過來叫做池化。池化的目的是壓縮張量的規模,張量可以理解成是矩陣。
池化的時候會將一個小窗口在矩陣上移動,每次會對小窗口內的元素進行計算,得到一個值。不同的池化方法體現在這里的計算的方式不同,比如常見的maxpooling,指的是每次從窗口中找出最大值的操作,再比如常見的sumpooling,則是進行求和計算。
我們可以看下下圖,就是一個典型的maxpooling的操作。
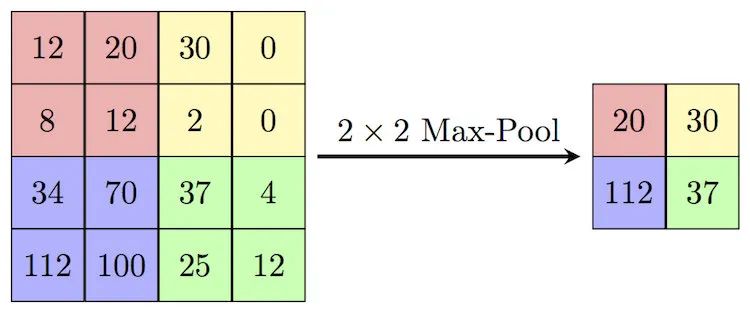
池化的時候,窗口的大小是2x2,移動的步長是2,每次都取出這2x2個數中的最大值,因此叫做最大值池化,英文就是maxpooling。
很明顯經過池化之后,矩陣的大小大大壓縮了,如果使用2x2的規模進行池化,得到的結果是原本的1/4。一般在卷積神經網絡當中,由于原始的輸入規模比較大(圖片或者是視頻),所以會反復進行池化,將原始的張量反復壓縮,提取出最核心的特征點。
那如果是一維的池化怎么操作呢,其實是一樣的,只不過窗口也換成了一維的而已。
比如說我們有這樣一個數組:[12, 20, 30, 0],窗口大小是2,步長是1,那么池化得到的結果是[20, 30, 30]。
介紹完了pooling的概念之后,我們再回到題目本身:給定一個長度為n的數組,再給定一個整數k,要求以k為窗口長度步長為1進行maxplooing之后的結果。
由于步長為1,所以我們一共要求n-k+1個最大整數,每次求最大整數如果采用遍歷的話,需要遍歷k個元素。那么整體就是,極端情況下,比如k=n/2時,問題的復雜度為。
這個只是暴力求解的方法,顯然在面試的時候這樣的答案是無法讓面試官滿意的,我們必須要想出更快的方法來。
我們簡單分析一下問題會發現,如果我們把窗口滑動看成是一次求解區間最大值的操作,那么這樣的操作數是固定的,也就是n-k+1,這個數字是固定的,是我們無法改變的。所以如果想要優化復雜度的話,只能從另外一個維度,也就是每次求解時的計算復雜度入手。
在暴力的方法下,我們每次遍歷k個元素,找到最大值。稍微分析一下就會發現,這里面有大量的重復。因為窗口的步長為1,假設某一次窗口內的元素是,移動之后的元素就是,當中有k-1個元素是重復的。
不難看出,對于每個元素來說,它最多會在k個窗口當中出現。對于每一個窗口我們都遍歷了一次,其實是沒有必要的,這當中存在大量的冗余。所以我們要做的就是想辦法優化它,盡量讓每個元素只會遍歷一次,或者是遍歷常數次。
你看,雖然我們現在還是沒有想出解法,但是我們通過分析問題,已經找到了方向,正在一步步逼近答案。
順著這個思路我們可以想到,我們可以維護上一個區間的最大值,我們假設這個最大值是m,然后和當前區間新加入的元素進行對比,大的那個就是當前區間的答案。
思路上看起來貌似可以,但細節上有一些問題。首先,上一個區間的最大值是可能會過期的。比如上一個區間剛好第一個元素最大,而當前區間第一個元素是,并不在當前區間里,所以是不能作為答案的。
我們是可以很容易判斷上一個區間的最大值有沒有過期的,但問題在于如果這個答案過期了,我們就抓瞎了,不知道哪個值是答案了。
那要怎么解決呢?
其實也很簡單,我們維護一個最大值會存在過期的問題,那干脆我們維護多個最大值嘛,我們維護多個答案,即使剛好因為區間移動有一個最大值過期了,還有第二個能夠頂上,這樣不就OK了嗎?
的確,這樣就搞定了,整個思路基本上就貫穿了。剩下的問題就是多個最大值如何維護的問題了,由于要維護多個值,我們自然需要一個數據結構來存儲,只用幾個變量是不行的了。
對于這個數據來說,我們讀到了新的數據時要很方便插入,對于之前過期的答案我們也要很方便移除,同時還要保證運行效率。在這幾個要求的結合之下,只剩下雙端隊列這一個選項了。
能想到雙端隊列,基本上這題就做出一大半了。
剩下的問題就是怎么使用它,由于我們的目的是找到最大值,并且是盡量快地找到合適的最大值,比較容易想到我們可以將雙端隊列設計成有序的。我們每次從最大值開始判斷,如果它還在窗口內,就是答案,如果已經超出了,就將它拋棄判斷第二大,循環往復直到找到答案。
最后還剩下兩個小問題,第一個小問題是我們怎么判斷最大值是否過期?
很簡單,我們在存儲的時候可以不用存元素的值,而存元素的下標。通過下標就可以很輕易判斷它是否在窗口內,如果不在,那么自然說明已經過期了。
第二個問題是,每次移動窗口之后讀入新的值如何更新?這也很簡單,我們可以從末尾開始替換掉雙端隊列中比它小的元素。這樣既更新了隊列,又保證了隊列的有序性。
閑言少敘,我們直接來看代碼:
voidget_max_pooling(intn,intk,vector<int>&nums,vector<int>&ans){
deque<int>dque;
//讀入前k個元素
for(inti=0;i-1;i++){
intu=nums[i];
//從隊列右側插入,替換掉比它小的元素,保證有序性
while(!dque.empty()&&u>nums[dque.back()]){
dque.pop_back();
}
//插入元素的下標而非具體的值
dque.push_back(i);
}
for(inti=k-1;iintu=nums[i];
//更新隊列,操作同上
while(!dque.empty()&&i-dque.front()>=k){
dque.pop_front();
}
//從隊首拿到第一個在窗口內的元素
while(!dque.empty()&&(u>nums[dque.back()]||i-dque.back()>=k)){
dque.pop_back();
}
dque.push_back(i);
ans.push_back(nums[dque.front()]);
}
}
從代碼來看,這題的代碼量并不大,實現起來也并不復雜,但勝在思路巧妙。也算是劍指offer當中一道非常經典出鏡率很高的題。
如果大家看不明白,可以結合一下代碼再回過頭去看下算法推導的過程。算法勝在思路而非答案。
好了,關于這道題就先聊到這里,祝大家日拱一卒。
原文標題:劍指算法題,一維數組求maxpooling
文章出處:【微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
審核編輯:湯梓紅
-
算法
+關注
關注
23文章
4630瀏覽量
93358 -
代碼
+關注
關注
30文章
4827瀏覽量
69055 -
數組
+關注
關注
1文章
417瀏覽量
26028
原文標題:劍指算法題,一維數組求maxpooling
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 如何對一維數組做maxpooling
如何對一維數組做maxpooling










評論