上堂課講到FIR濾波器的線性相位特點，分析了線性相位帶來的延時特性。本堂課繼續講解FIR濾波器的幅度特性，再理論聯系實際的看看FIR濾波器到底長什么樣？有什么用？聽我慢慢道來。

在MATLAB函數中，有FIR1和FIR2函數，前者是用于處理一維數組，后者是用于二維數組的處理，哪些地方能用二位數組處理呢？圖像處理中會用到，這里提一下，能讓同學們有個了解。

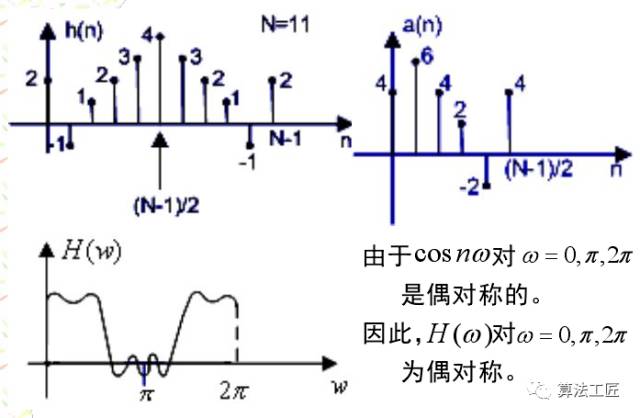
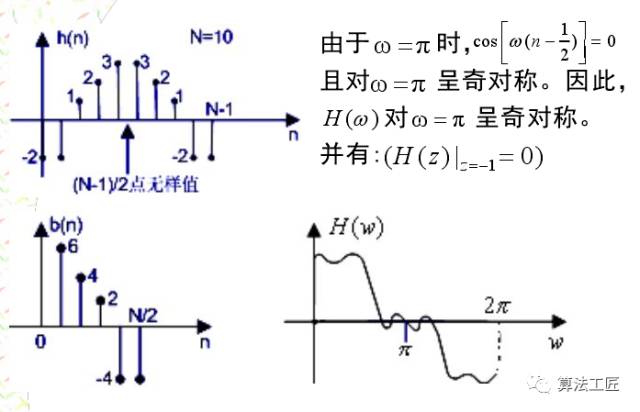
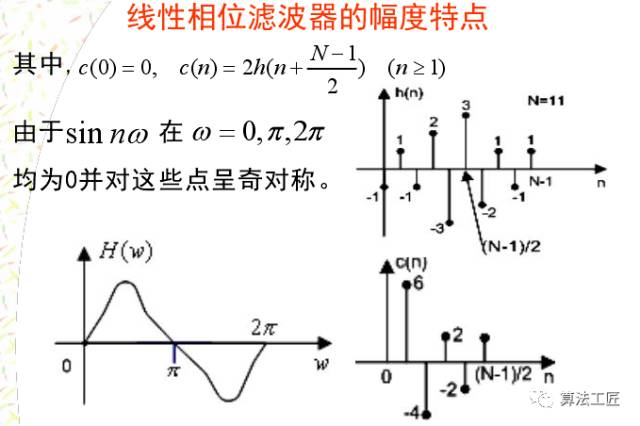
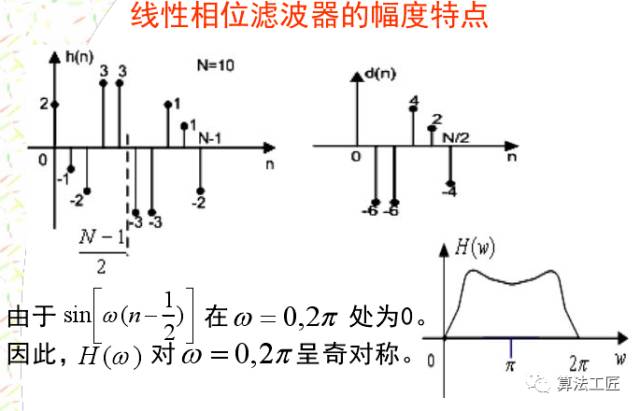
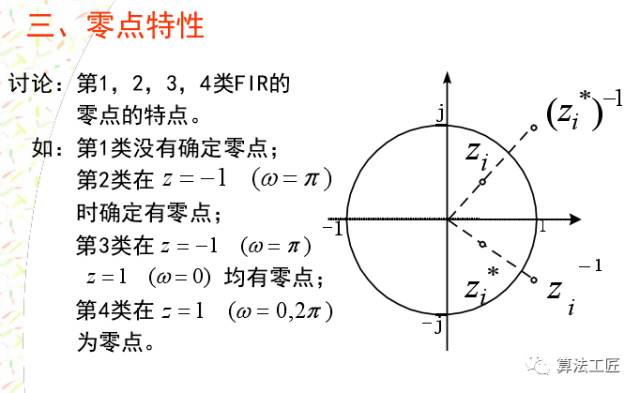
講完這些理論，來一些涉及程序仿真的內容，看看理論能不能聯系實際！

信號中經常混有各種復雜成分，有需要的成分，也有不需要的成分。很多信號分析都是基于濾波器而進行， 因此數字濾波器占有極其重要的地位 。數字濾波器是具有一定傳輸選擇特性的數字信號處理裝置，其輸入與輸出均為數字信號實質上是一個由有限精度算法實現的線性時不變離散系統。

它的基本工作原理是利用離散系統特性對系統輸入信號進行加工和變換，改變輸入序列的頻譜或信號波形，讓有用頻率的信號分量通過，抑制無用的信號分量輸出。數字濾波器和模擬濾波器有著相同的濾波概念，根據其頻率響應特性可分為低通、高通、帶通、帶阻等類型。

與模擬濾波器相比，數字濾波器除了具有數字信號處理固有優點外，還有精度高、穩定性好、靈活性強等優點。FIR濾波器具有線性相位，但它的傳遞函數的極點固定在原點，只能通過改變零點位置來改變性能，為了達到高的選擇性必須用較高的階數。

對于同樣的濾波器設計指標，FIR濾波器要求的階數可能比 IIR濾波器高10倍以上。

由于 FIR 數字濾波器具有嚴格的相位特性，對于信號處理和數據傳輸是很重要的。目前 FIR 濾波器的設計方法主要有三種：窗函數法、頻率抽樣法和優化設計（切比雪夫逼近）方法。我們重點學習窗函數法。

看看結果吧！

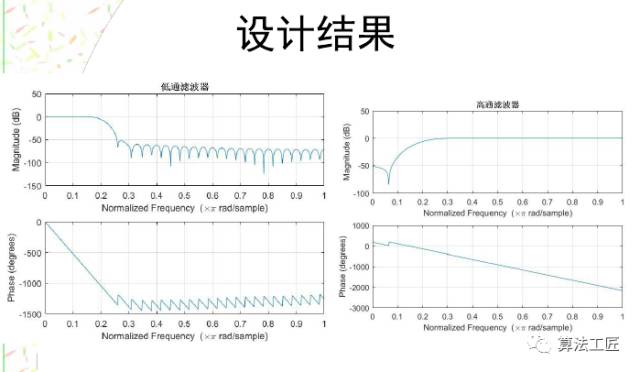
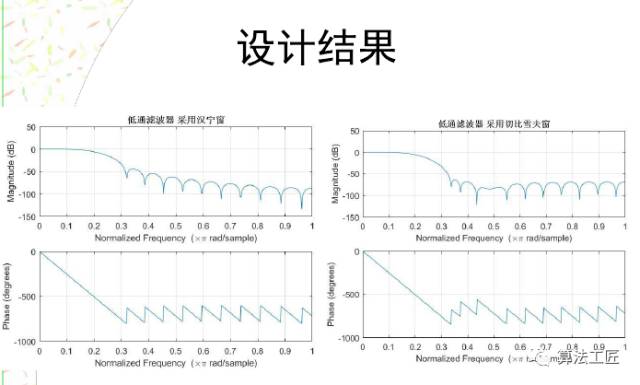
之前對fir2函數的描述有錯誤，這個函數不是用來處理二維數組的！

它可以用于設計有任意頻率響應的加窗FIR濾波器。

對標準的低通、帶通、高通和帶阻濾波器的設計可使用fir1函數。

語法：b=fir2（n，f，m）

設計出一個n階的FIR濾波器，其濾波器的頻率特性由參數f和m決定。

參數f為頻率點矢量，且f∈［0，1］，f=1對應于0.5fs。

矢量f按升序排列，且第一個元素必須是0，最后一個必須為1，并可以包含重復的頻率點。

矢量m中包含了與f相對應的期望得到的濾波器的幅度。f為歸一化頻率向量。

舉例如下：設計一個100階的低通濾波器。運行一下代碼，看看能出什么結果？

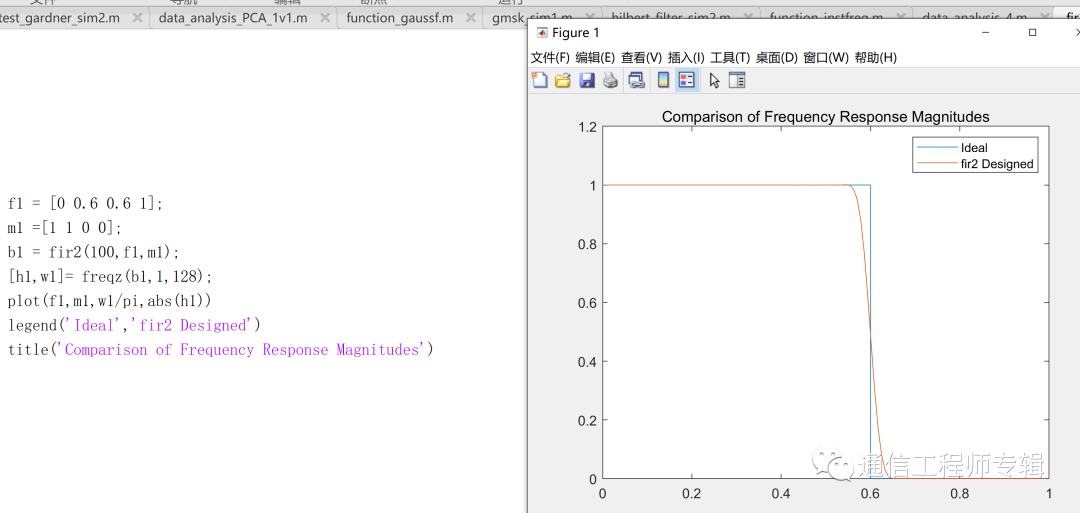
如果要求設計一個奇怪形狀的濾波器呢？

比如設計一個80階的FIR濾波器，要求濾波器0到π/4的幅度響應為0 ，π/4到π/2的幅度響應為1/4，π/2到3π/4的幅度響應為0，3π/4到1的幅度響應為1。采用切比雪夫窗。該怎么寫程序呢？

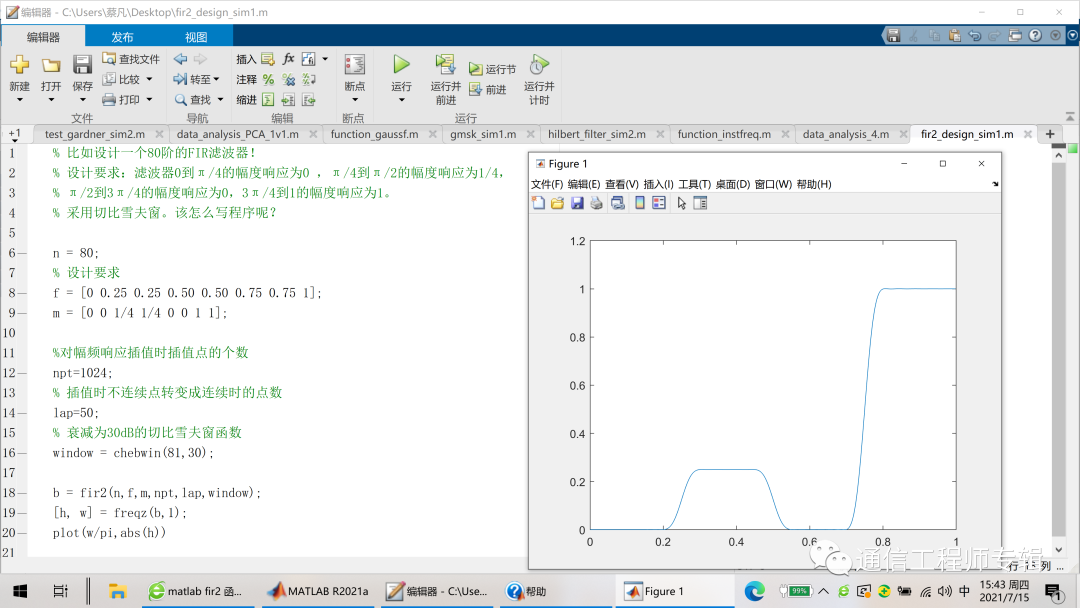
有程序有圖就有真正的理解！

編輯：jq