The pooling operation used in convolutional neural networks is a big mistake and the fact that it works so well is a disaster. ——Hinton
先引用深度學(xué)習(xí)三巨頭之一Geoffrey Hinton(杰弗里·辛頓)的名人名言作為開(kāi)端.
CNN是現(xiàn)在十分火熱的模型,首先我們都知道,通過(guò)pooling層能夠?qū)W到部分高階特征,比如對(duì)于人臉而言可以激活識(shí)別到鼻子 ,嘴巴 ,眼睛 等。
大神們看到CNN模型的強(qiáng)大開(kāi)始進(jìn)行人性本質(zhì)的思索,那么它有什么搞不懂的時(shí)候咩?
答:確實(shí)有。
具體來(lái)說(shuō),pooling并不能夠?qū)W到這些特征具體是從哪一層特征學(xué)到的,也就意味著會(huì)損失高階特征之間的相互空間關(guān)系,空間層級(jí)信息無(wú)法獲取到。也就是混亂的 并不能夠表征一張人臉。這就是pooling層存在的缺陷。
好吧,簡(jiǎn)言之就是臉盲。
我們接著來(lái)看,計(jì)算機(jī)得到圖像的過(guò)程是一層一層,從圖像的內(nèi)部表示到整體圖像表示。但是人對(duì)圖像的認(rèn)識(shí)恰恰相反!
科普時(shí)間到:
人腦對(duì)圖像的認(rèn)識(shí)關(guān)鍵的點(diǎn)在于圖像位置姿態(tài)的認(rèn)識(shí),也就是即便圖像進(jìn)行了旋轉(zhuǎn),平移人腦依然可以認(rèn)識(shí)圖像,而計(jì)算機(jī)卻不行。因此提出膠囊網(wǎng)絡(luò)CapsNet。
那么我們來(lái)正經(jīng)地看看到底什么是膠囊(總之不是吃的那個(gè)小藥丸 )
一:膠囊定義
膠囊(Capsule)是一個(gè),包含多個(gè)神經(jīng)元的特征載體。每個(gè)神經(jīng)元可以表示圖像中出現(xiàn)的特定實(shí)體的各種屬性,比如姿態(tài)(位置,大小,方向),紋理,變形等。
膠囊以向量的形式封裝特征的各種屬性表示。數(shù)值就是這個(gè)屬性表示存在的概率,會(huì)隨著特征的空間變化而變化,向量的長(zhǎng)度保持不變的話,整個(gè)膠囊表征的高層特征就保持一致,這就是Hinton提出的活動(dòng)等變性,這個(gè)不變性的意義高于pooling的不變性。

聽(tīng)懂以上概念后,大神小伙伴們就接著來(lái)看它的運(yùn)算過(guò)程吧。
二:膠囊卷積運(yùn)算過(guò)程
1. 輸入向量的矩陣乘法
2. 輸入向量的標(biāo)量加權(quán)
3. 加權(quán)輸入向量之和
4. 向量到向量的非線性變換
總之就是先這樣,再那樣就好啦~
好了,回歸干貨:
u1、u2、u3就是來(lái)自下層的3個(gè)膠囊 ,向量的長(zhǎng)度編碼了下層膠囊相應(yīng)特征的概率。
那么
w1j、w2j、w3j 就能夠編碼高層特征和低層特征之間的空間關(guān)系。
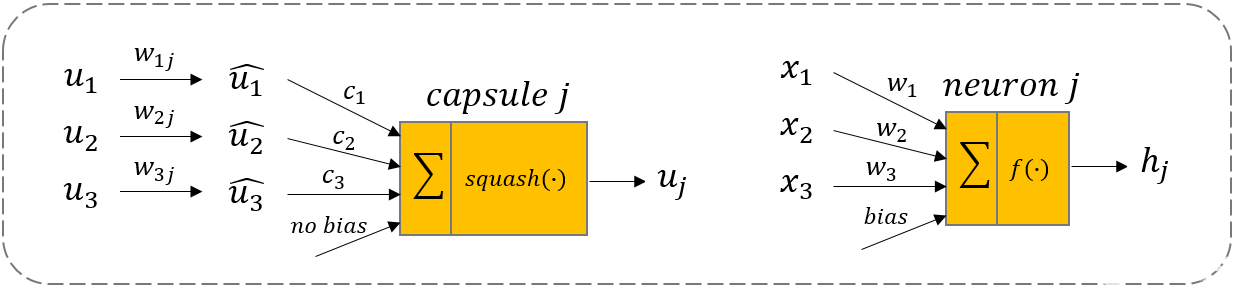
神經(jīng)網(wǎng)絡(luò)是通過(guò)反向傳播來(lái)學(xué)習(xí)參數(shù),而膠囊網(wǎng)絡(luò)是通過(guò)“動(dòng)態(tài)路由”算法來(lái)進(jìn)行更新。
低層膠囊需要決定它的輸出是向哪個(gè)高層膠囊輸出。通過(guò)學(xué)習(xí)cici才能夠激活是向哪個(gè)方向的膠囊進(jìn)行映射。
所以對(duì)于動(dòng)態(tài)路由算法就是ujuj服從的某個(gè)分布,每層膠囊會(huì)相對(duì)聚集,那么接下來(lái)學(xué)習(xí)的低層膠囊向哪個(gè)高層膠囊映射,就是通過(guò)這種預(yù)測(cè)更接近的膠囊聚集來(lái)判斷的。
接下來(lái)向量到向量的非線性變換就是用了一個(gè)新穎的非線性激活函數(shù),接收一個(gè)向量,然后在不改變方向的前提下,壓縮它的長(zhǎng)度到1以下。就是squash(?):
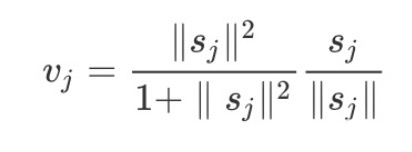
為了清晰地讓大家理解,整來(lái)了一張圖,更形象的描述整個(gè)學(xué)習(xí)過(guò)程:??
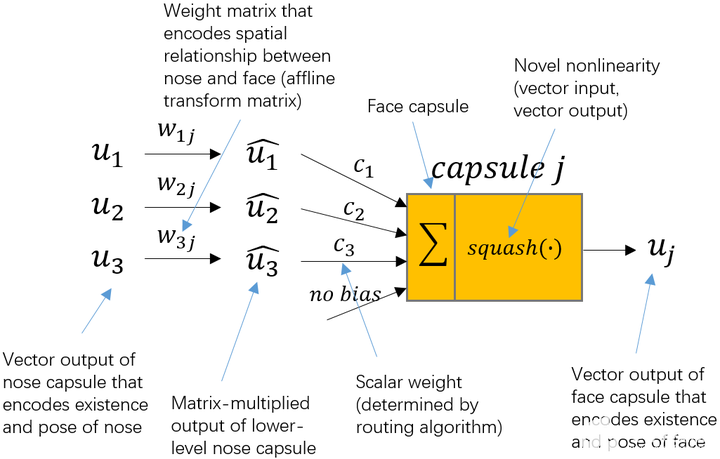
怎么樣,是不是看著一下子就通透了起來(lái)呀^ ^
三:動(dòng)態(tài)路由算法
好了我們繼續(xù)往下肝??

從上述算法過(guò)程就能夠明白,輸入為低層所有的膠囊線性變換的輸出$hat{u}_{j|i}$以及路由迭代次數(shù)$r$和層$l$ 。定義了一個(gè)零時(shí)變量$b_{ij}$初始化為0,在迭代過(guò)程中會(huì)更新,$c_i leftarrow softmax(b_i)$就是低層膠囊所有的權(quán)重。
舉個(gè)簡(jiǎn)單的小例子??
權(quán)重分配過(guò)程:$b_{ij }$初始化為0,第一次迭代,假設(shè)有3個(gè)低層膠囊,2個(gè)高層膠囊,那么$c_{ij}$都會(huì)等于0.5,所有的權(quán)重$c_{ij}$都相等。
隨著迭代才會(huì)使得低層膠囊可以根據(jù)這個(gè)權(quán)重指向?qū)?yīng)的高層膠囊。$s_j leftarrow sum_i c_{ij} hat{mathbf{u}}_{j|i}$ 就是對(duì)每一個(gè)膠囊做一個(gè)線性組合,然后通過(guò)$squash$函數(shù)得到傳遞方向不變的權(quán)重向量。最后更行相應(yīng)的權(quán)重$b_{ij}$。
(嗯!大神們是不是覺(jué)得很簡(jiǎn)單(o^^o))
高層膠囊$j$的當(dāng)前輸出和從低層膠囊 $i$出接收的輸入做點(diǎn)積,再加上上一輪的權(quán)重$b_{ij}$,得到更新的$b_{ij}$。點(diǎn)積可以表征膠囊之間的相似性,其實(shí)也就是將低層膠囊的特征學(xué)習(xí)過(guò)來(lái),這就與$CNN$的學(xué)習(xí)效果一致。
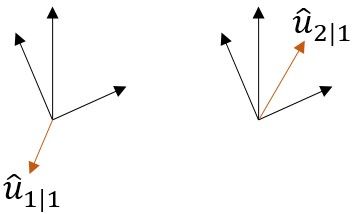
明顯從上圖就可以看出,$hat{u}{1|1}$和上面黑色的向量不相似,$hat{u}{2|1}$就和上面黑色的向量是相似的,那么路由權(quán)重$c_{11}$會(huì)降低,而$c_{12}$會(huì)增大。從而低層膠囊的學(xué)習(xí)就能有最優(yōu)的匹配。
綜上!一篇簡(jiǎn)單的科普教學(xué)文就結(jié)束啦,誰(shuí)用誰(shuí)知道!
所以————
聽(tīng)懂掌聲!
那下篇我們來(lái)簡(jiǎn)單聊聊「相似三連」:DNN、RNN、CNN里的RNN吧!(遞歸神經(jīng)網(wǎng)絡(luò))
編輯:jq
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4779瀏覽量
101171 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4346瀏覽量
62973 -
神經(jīng)元
+關(guān)注
關(guān)注
1文章
363瀏覽量
18511 -
動(dòng)態(tài)路由
+關(guān)注
關(guān)注
0文章
16瀏覽量
23141
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
小鵬大眾將攜手合力打造中國(guó)最大的超快充網(wǎng)絡(luò)
基于恩智浦 MCX N947 MCU 通過(guò) NPU 實(shí)現(xiàn) AI 咖啡膠囊識(shí)別方案

超六類網(wǎng)絡(luò)面板怎么接線
超網(wǎng)和無(wú)類間路由是什么?

超六類有沒(méi)有百兆
卷積神經(jīng)網(wǎng)絡(luò)與循環(huán)神經(jīng)網(wǎng)絡(luò)的區(qū)別
膠囊字符機(jī)器視覺(jué)檢測(cè)識(shí)別方案定制

超六類非屏蔽雙絞線在網(wǎng)絡(luò)中的地位
矢量網(wǎng)絡(luò)分析儀的關(guān)鍵技術(shù)指標(biāo)解讀
超融合架構(gòu)解決方案
生醫(yī)應(yīng)用的磁控膠囊機(jī)器人,實(shí)現(xiàn)多模態(tài)響應(yīng)與多功能集成




 超干貨解讀膠囊網(wǎng)絡(luò)
超干貨解讀膠囊網(wǎng)絡(luò)












評(píng)論