摘要：在對FFT（快速傅立葉變換）算法進行研究的基礎上，描述了用FPGA實現FFT的方法，并對其中的整體結構、蝶形單元及性能等進行了分析。 傅立葉變換是數字信號處理中的基本操作，廣泛應用于表述及分析離散時域信號領域。但由于其運算量與變換點數Ｎ的平方成正比關系，因此，在Ｎ較大時，直接應用ＤＦＴ算法進行譜變換是不切合實際的。然而，快速傅立葉變換技術的出現使情況發生了根本性的變化。本文主要描述了采用ＦＰＧＡ來實現２ｋ／４ｋ／８ｋ點ＦＦＴ的設計方法。

１整體結構

一般情況下，Ｎ點的傅立葉變換對為： 其中，ＷＮ＝ｅｘｐ（－２ ｐｉ／Ｎ）。Ｘ（ｋ）和ｘ（ｎ）都為復數。與之相對的快速傅立葉變換有很多種，如ＤＩＴ（時域抽取法）、ＤＩＦ（頻域抽取法）、Ｃｏｏｌｅｙ－Ｔｕｋｅｙ和Ｗｉｎｏｇｒａｄ等。對于２ｎ傅立葉變換，Ｃｏｏｌｅｙ－Ｔｕｋｅｙ算法可導出ＤＩＴ和ＤＩＦ算法。

本文運用的基本思想是Ｃｏｏｌｅｙ－Ｔｕｋｅｙ算法，即將高點數的傅立葉變換通過多重低點數傅立葉變換來實現。雖然ＤＩＴ與ＤＩＦ有差別，但由于它們在本質上都是一種基于標號分解的算法，故在運算量和算法復雜性等方面完全一樣，而沒有性能上的優劣之分，所以可以根據需要任取其中一種，本文主要以ＤＩＴ方法為對象來討論。

Ｎ＝８１９２點ＤＦＴ的運算表達式為： 式中，ｍ＝（４ｎ１＋ｎ２）（２０４８ｋ１＋ｋ２）（ｎ＝４ｎ１＋ｎ２，ｋ＝２０４８ｋ１＋ｋ２）其中ｎ１和ｋ２可取０，１，．．．，２０４７，ｋ１和ｎ２可取０，１，２，３。 由式（３）可知，８ｋ傅立葉變換可由４×２ｋ的傅立葉變換構成。

同理，４ｋ傅立葉變換可由２×２ｋ的傅立葉變換構成。而２ｋ傅立葉變換可由１２８×１６的傅立葉變換構成。１２８的傅立葉變換可進一步由１６×８的傅立葉變換構成，歸根結底，整個傅立葉變換可由基２、基４的傅立葉變換構成。２ｋ的ＦＦＴ可以通過５個基４和１個基２變換來實現；

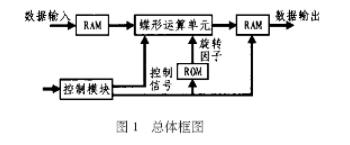
４ｋ的ＦＦＴ變換可通過６個基４變換來實現；８ｋ的ＦＦＴ可以通過６個基４和１個基２變換來實現。也就是說：ＦＦＴ的基本結構可由基２／４模塊、復數乘法器、存儲單元和存儲器控制模塊構成，其整體結構如圖１所示。 圖１中，ＲＡＭ用來存儲輸入數據、運算過程中的中間結果以及運算完成后的數據，ＲＯＭ用來存儲旋轉因子表。蝶形運算單元即為基２／４模塊，控制模塊可用于產生控制時序及地址信號，以控制中間運算過程及最后輸出結果。

２蝶形運算器的實現

基４和基２的信號流如圖２所示。

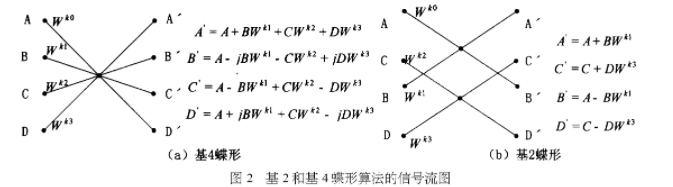
圖中，若Ａ＝ｒ０＋ｊ＊ｉ０，Ｂ＝ｒ１＋ｊ＊ｉ１，Ｃ＝ｒ２＋ｊ＊ｉ２，Ｄ＝ｒ３＋ｊ＊ｉ３是要進行變換的信號，Ｗｋ０＝ｃ０＋ｊ＊ｓ０＝１，Ｗｋ１＝ｃ１＋ｊ＊ｓ１，Ｗｋ２＝ｃ２＋ｊ＊ｓ２，Ｗｋ３＝ｃ３＋ｊ＊ｓ３為旋轉因子，將其分別代入圖２中的基４蝶形運算單元，

則有： Ａ′＝［ｒ０＋（ｒ１×ｃ１－ｉ１×ｓ１）＋（ｒ２×ｃ２－ｉ２×ｓ２）＋（ｒ３×ｃ３－ｉ３×ｓ３）］＋ｊ［ｉ０＋（ｉ１×ｃ１＋ｒ１×ｓ１）＋（ｉ２×ｃ２＋ｒ２×ｓ２）＋（ｉ３×ｃ３＋ｒ３×ｓ３）］？？ （４） Ｂ′＝［ｒ０＋（ｉ１×ｃ１＋ｒ１×ｓ１）－（ｒ２×ｃ２－ｉ２×ｓ２）－（ｉ３×ｃ３＋ｒ３×ｓ３）］＋ｊ［ｉ０－（ｒ１×ｃ１－ｉ１×ｓ１）－（ｉ２×ｃ２＋ｒ２×ｓ２）＋（ｒ３×ｃ３－ｉ３×ｓ３）］ （５） Ｃ′＝［ｒ０－（ｒ１×ｃ１－ｉ１×ｓ１）＋（ｒ２×ｃ２－ｉ２×ｓ２）－（ｒ３×ｃ３－ｉ３×ｓ３）］＋ｊ［ｉ０－（ｉ１×ｃ１＋ｒ１×ｓ１）＋（ｉ２×ｃ２＋ｒ２×ｓ２）－（ｉ３×ｃ３＋ｒ３×ｓ３）］ （６） Ｄ′＝［ｒ０－（ｉ１×ｃ１＋ｒ１×ｓ１）－（ｒ２×ｃ２－ｉ２×ｓ２）＋（ｉ３×ｃ３＋ｒ３×ｓ３）］＋ｊ［ｉ０＋（ｒ１×ｃ１－ｉ１×ｓ１）－（ｉ２×ｃ２＋ｒ２×ｓ２）－（ｒ３×ｃ３－ｉ３×ｓ３）］？？ （７）

而在基２蝶形中，Ｗｋ０和Ｗｋ２的值均為１，這樣，將Ａ，Ｂ，Ｃ和Ｄ的表達式代入圖２中的基２運算的四個等式中，則有： Ａ′＝ｒ０＋（ｒ１×ｃ１－ｉ１×ｓ１）＋ｊ［ｉ０＋（ｉ１×ｃ１＋ｒ１×ｓ１）］？？ （８） Ｂ′＝ｒ０－ （ｒ１×ｃ１－ｉ１×ｓ１）＋ｊ［ｉ０－（ｉ１×ｃ１＋ｒ１×ｓ１）］ （９） Ｃ′＝ｒ２＋（ｒ３×ｃ３－ｉ３×ｓ３）＋ｊ［ｉ０＋（ｉ３×ｃ３＋ｒ３×ｓ３）］？？ （１０） Ｄ′＝ｒ２－（ｒ３×ｃ３－ｉ３×ｓ３）＋ｊ［ｉ０－（ｉ３×ｃ３＋ｒ３×ｓ３）］？？ （１１） 在上述式（４）～（１１）中有很多類同項，如ｉ１×ｃ１＋ｒ１×ｓ１和ｒ１×ｃ１－ｉ１×ｓ１等，

它們僅僅是加減號的不同，其結構和運算均類似，這就為簡化電路提供了可能。同時，在蝶形運算中，復數乘法可以由實數乘法以一定的格式來表示，這也為設計復數乘法器提供了一種實現的途徑。 以基４為例，在其運算單元中，實際上只需做三個復數乘法運算，即只須計算ＢＷｋ１、ＣＷｋ２和ＤＷｋ３的值即可。

這樣在一個基４蝶形單元里面，最多只需要３個復數乘法器就可以了。在實際過程中，在不提高時鐘頻率下，只要將時序控制好？煴憧衫？用流水線（Ｐｉｐｅｌｉｎｅ）技術并只用一個復數乘法器就可完成這三個復數乘法，大大節省了硬件資源。

３ＦＦＴ的地址

ＦＦＴ變換后輸出的結果通常為一特定的倒序，因此，幾級變換后對地址的控制必須準確無誤。 倒序的規律是和分解的方式密切相關的，以基８為例，其基本倒序規則如下： 基８可以用２×２×２**基２變換來表示，則其輸入順序則可用二進制序列（ｎ１ ｎ２ ｎ３）來表示，變換結束后，其順序將變為（ｎ３ ｎ２ ｎ１）。

如：Ｘ？煟埃保保？→ ｘ？煟保保埃牐？即輸入順序為３，輸出時順序變為６。 更進一步，對于基１６的變換，可由２×２×２×２，４×４，４×２×２等形式來構成，相對于不同的分解形式，往往會有不同的倒序方式。以４×４為例，其輸入順序可以用二進制序列（ｎ１ ｎ２ ｎ３ ｎ４）來表示變換結束后，其順序可變為（（ｎ３ ｎ４）（ｎ１ ｎ２））。

如：Ｘ？煟埃保保保？→ ｘ？煟保保埃保牎＜詞淙胨承蛭？７，輸出時順序變為１３。 在２ｋ／４ｋ／８ｋ的傅立葉變換中，由于要經過多次的基４和基２運算，因此，從每次運算完成后到進入下一次運算前，應對運算的結果進行倒序，以保證運算的正確性。

４旋轉因子

Ｎ點傅立葉變換的旋轉因子有著明顯的周期性和對稱性。其周期性表現為： FFT之所以可使運算效率得到提高，就是利用 ＦＦＴ之所以可使運算效率得到提高，就是利用了對稱性和周期性把長序列的ＤＦＴ逐級分解成幾個序列的ＤＦＴ，并最終以短點數變換來實現長點數變換。

根據旋轉因子的對稱性和周期性，在利用ＲＯＭ存儲旋轉因子時，可以只存儲旋轉因子表的一部分，而在讀出時增加讀出地址及符號的控制，這樣可以正確實現ＦＦＴ。因此，充分利用旋轉因子的性質，可節省７０％以上存儲單元。 實際上，由于旋轉因子可分解為正、余弦函數的組合，故ＲＯＭ中存的值為正、余弦函數值的組合。

對２ｋ／４ｋ／８ｋ的傅立葉變換來說，只是對一個周期進行不同的分割。由于８ｋ變換的旋轉因子包括了２ｋ／４ｋ的所有因子，因此，實現時只要對讀ＲＯＭ的地址進行控制，即可實現２ｋ／４ｋ／８ｋ變換的通用。

５存儲器的控制

因ＦＦＴ是為時序電路而設計的，因此，控制信號要包括時序的控制信號及存儲器的讀寫地址，并產生各種輔助的指示信號。同時在計算模塊的內部，為保證高速，所有的乘法器都須始終保持較高的利用率。這意味著在每一個時鐘來臨時都要向這些單元輸入新的操作數，而這一切都需要控制信號的緊密配合。

為了實現ＦＦＴ的流形運算，在運算的同時，存儲器也要接收數據。這可以采用乒乓ＲＡＭ的方法來完成。

這種方式決定了實現ＦＦＴ運算的最大時間。對于４ｋ操作，其接收時間為４０９６個數據周期，這樣？煟疲疲緣淖畬笤慫閌奔渚褪牽矗埃梗陡鍪？據周期。另外，由于輸入數據是以一定的時鐘為周期依次輸入的，故在進行內部運算時，可以用較高的內部時鐘進行運算，然后再存入ＲＡＭ依次輸出。

為節省資源，可對存儲數據ＲＡＭ采用原址讀出原址寫入的方法，即在進行下一級變換的同時，首先應將結果回寫到讀出數據的ＲＡＭ存貯器中；而對于ＲＯＭ，則應采用與運算的數據相對應的方法來讀出存儲器中旋轉因子的值。

在２ｋ／４ｋ／８ｋ傅立葉變換中，要實現通用性，控制器是最主要的模塊。２ｋ、４ｋ、８ｋ變換具有不同的內部運算時間和存儲器地址，在設計中，針對不同的點數應設計不同的存儲器存取地址，同時，在完成變換后，還要對開始輸出有用信號的時刻進行指示。

６硬件的選擇

本設計的硬件實現選用的是現場可編程門陣列（ＦＰＧＡ）來滿足較高速度的需要。本系統在設計時選用的是ＡＬＴＥＲＡ公司的ＳＴＲＡＴＩＸ芯片，該芯片中包含有ＤＳＰ單元，可以完成較為耗費資源的乘法器單元。

同時，該器件也包含有大量存儲單元，從而可保證旋轉因子的精度。 除了一些專用引腳外，ＦＰＧＡ上幾乎所有的引腳均可供用戶使用，這使得ＦＰＧＡ信號處理方案具有非常好的Ｉ／Ｏ帶寬。大量的Ｉ／Ｏ引腳和多塊存儲器可使設計獲得優越的并行處理性能。其獨立的存儲塊可作為輸入／工作存儲區和結果的緩存區，這使得Ｉ／Ｏ可與ＦＦＴ計算同時進行。

在實現的時間方面，該設計能在４０９６個時鐘周期內完成一個４０９６點的ＦＦＴ。若采用１０ＭＨｚ的輸入時鐘，其變換時間在２００μｓ左右。而由于最新的ＦＰＧＡ使用了ＭｕｌｔｉＴｒａｃｋ互連技術，故可在２５０ＭＨｚ以下頻率穩定地工作，同時，ＦＦＴ的實現時間也可以大大縮小。

ＦＦＴ運算結果的精度與輸入數據的位數及運算過程中的位數有關，同時和數據的表示形式也有很大關系。一般來說，浮點方式比定點方式精度高。而在定點計算中，存儲器數據的位數越大，運算精度越高，使用的存儲單元和邏輯單元也越多。在實際應用中，應根據實際情況折衷選擇精度和資源。

本設計通過ＭＡＴＬＡＢ進行仿真證明：其實現的變換結果與ＭＡＴＬＡＢ工具箱中的ＦＦＴ函數相比，信噪比可以達到６５ｄｂ以上，完全可以滿足一般工程的實際應用要求。

作者：連冰，宮豐奎，張力，李兵兵

編輯：jq