卷積神經網絡結構

一個卷積神經網絡主要由以下5種結構組成：

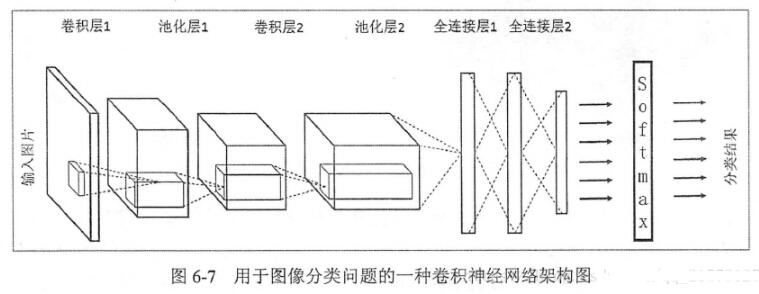
1.輸入層。輸入層是整個神經網絡的輸入，在處理圖像的卷積神經網絡中，它一般代表了一張圖片的像素矩陣。比如在圖6-7中，最左側的三維矩陣的長和寬代表了圖像的大小，而三維矩陣的深度代表了圖像的色彩通道（channel）。比如黑白圖片的深度為1，而在RGB色彩模式下，圖像的深度為3。從輸入層開始，卷積神經網絡通過不同的神經網絡結構下將上一層的三維矩陣轉化為下一層的三維矩陣轉化為下一層的三維矩陣，直到最后的全連接層。

2.卷積層。從名字就可以看出，卷積層是一個卷積神經網絡中最重要的部分。和傳統全連接層不同，卷積層中的每一個節點的輸入只是上一層神經網絡中的一小塊，這個小塊的大小有3*3或者5*5。卷積層試圖將神經網絡中的每一個小塊進行更加深入的分析從而得到抽象程度更高的特征。一般來說，通過卷積層處理的節點矩陣會變得更深，所以圖6-7中可以看到經過卷積層之后的節點矩陣的深度會增加。

3.池化層。池化層神經網絡不會改變三維矩陣的深度，但是它可以縮小矩陣的大小。池化操作可以認為是將一張分辨率較高的圖片轉化為分辨率較低的圖片。通過池化層，可以進一步縮小最后全連接層中節點的個數，從而達到減少整個神經網絡中的參數的目的。

4.全連接層。如圖6-7所示，在經過多輪卷積層和池化層處理之后，在卷積神經網絡的最后一般會由1到2個全連接 層來給出最后的分類結果。經過幾輪的卷積層和池化層的處理之后，可以認為圖像中的信息已被抽象成了信息含量更高的特征。我們可以將卷積層和池化層看成自動圖像特征提取的過程。在特征提取完成之后，仍然需要使用全連接層來完成分類任務。

5.Softmax層。Softmax層主要用于分類問題。經過Softmax層，可以得到當前樣例中屬于不同種類的概率分布情況。

卷積神經網絡訓練過程

卷積神經網絡的訓練過程分為兩個階段。第一個階段是數據由低層次向高層次傳播的階段，即前向傳播階段。另外一個階段是，當前向傳播得出的結果與預期不相符時，將誤差從高層次向底層次進行傳播訓練的階段，即反向傳播階段。訓練過程如圖4-1所示。訓練過程為：

1、網絡進行權值的初始化；

2、輸入數據經過卷積層、下采樣層、全連接層的向前傳播得到輸出值；

3、求出網絡的輸出值與目標值之間的誤差；

4、當誤差大于我們的期望值時，將誤差傳回網絡中，依次求得全連接層，下采樣層，卷積層的誤差。各層的誤差可以理解為對于網絡的總誤差，網絡應承擔多少；當誤差等于或小于我們的期望值時，結束訓練。

5、根據求得誤差進行權值更新。然后在進入到第二步。

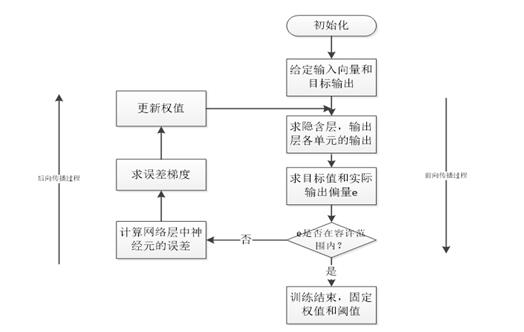
圖4-1卷積神經網絡的訓練過程

1.1卷積神經網絡的前向傳播過程

在前向傳播過程中，輸入的圖形數據經過多層卷積層的卷積和池化處理，提出特征向量，將特征向量傳入全連接層中，得出分類識別的結果。當輸出的結果與我們的期望值相符時，輸出結果。

1.1.1卷積層的向前傳播過程

卷積層的向前傳播過程是，通過卷積核對輸入數據進行卷積操作得到卷積操作。數據在實際的網絡中的計算過程，我們以圖3-4為例，介紹卷積層的向前傳播過程。其中一個輸入為15個神經元的圖片，卷積核為2×2×1的網絡，即卷積核的權值為W1，W2，W3，W4。那么卷積核對于輸入數據的卷積過程，如下圖4-2所示。卷積核采用步長為1的卷積方式，卷積整個輸入圖片，形成了局部感受野，然后與其進行卷積算法，即權值矩陣與圖片的特征值進行加權和（再加上一個偏置量），然后通過激活函數得到輸出。

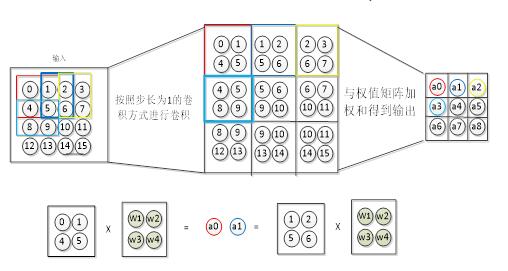
圖4-2圖片深度為1，卷積層的向前傳播過程

而在圖3-4中，圖片深度為2時，卷積層的向前傳播過程如圖4-3所示。輸入的圖片的深度為4×4×2，卷積核為2×2×2，向前傳播過程為，求得第一層的數據與卷積核的第一層的權值的加權和，然后再求得第二層的數據與卷積核的第二層的權值的加權和，兩層的加權和相加得到網絡的輸出。

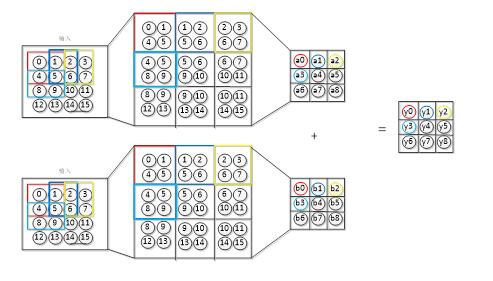
圖4-3圖片深度為2，卷積層的向前傳播過程

1.1.2下采樣層的向前傳播過程

上一層（卷積層）提取的特征作為輸入傳到下采樣層，通過下采樣層的池化操作，降低數據的維度，可以避免過擬合。如圖4-4中為常見的池化方式示意。最大池化方法也就是選取特征圖中的最大值。均值池化則是求出特征圖的平均值。隨機池化方法則是先求出所有的特征值出現在該特征圖中的概率，然后在來隨機選取其中的一個概率作為該特征圖的特征值，其中概率越大的選擇的幾率越大。

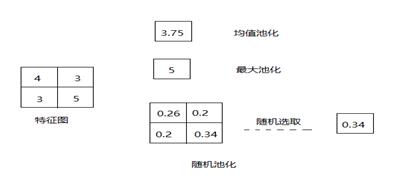
圖4-4池化操作示意圖

1.1.3全連接層的向前傳播過程

特征圖進過卷積層和下采樣層的特征提取之后，將提取出來的特征傳到全連接層中，通過全連接層，進行分類，獲得分類模型，得到最后的結果。圖4-5為一個三層的全連接層。假設卷積神經網絡中，傳入全連接層的特征為x1，x2。則其在全連接層中的向前傳播過程如圖4-5所示。第一層全連接層有3個神經元y1，y2，y3。這三個節點的權值矩陣為W，其中b1，b2，b3分別為節點y1，y2，y3的偏置量。可以看出，在全連接層中，參數的個數=全連接層中節點的個數×輸入的特征的個數+節點的個數（偏置量）。其向前傳遞過程具體如圖所示，得到輸出矩陣后，經過激勵函數f（y）的激活，傳入下一層。

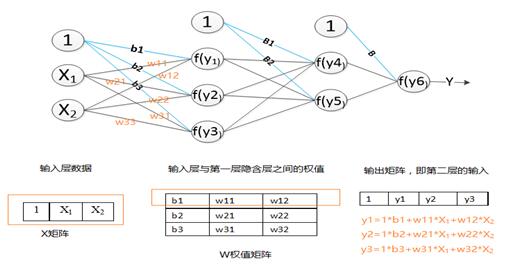
圖4-5全連接層的向前傳播過程

1.2卷積神經網絡的反向傳播過程

當卷積神經網絡輸出的結果與我們的期望值不相符時，則進行反向傳播過程。求出結果與期望值的誤差，再將誤差一層一層的返回，計算出每一層的誤差，然后進行權值更新。該過程的主要目的是通過訓練樣本和期望值來調整網絡權值。誤差的傳遞過程可以這樣來理解，首先，數據從輸入層到輸出層，期間經過了卷積層，下采樣層，全連接層，而數據在各層之間傳遞的過程中難免會造成數據的損失，則也就導致了誤差的產生。而每一層造成的誤差值是不一樣的，所以當我們求出網絡的總誤差之后，需要將誤差傳入網絡中，求得該各層對于總的誤差應該承擔多少比重。

反向傳播的訓練過程的第一步為計算出網絡總的誤差：求出輸出層n的輸出a（n）與目標值y之間為誤差。計算公式為：

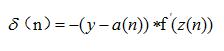
其中，為激勵函數的導函數的值。

1.2.1全連接層之間的誤差傳遞

求出網絡的總差之后，進行反向傳播過程，將誤差傳入輸出層的上一層全連接層，求出在該層中，產生了多少誤差。而網絡的誤差又是由組成該網絡的神經元所造成的，所以我們要求出每個神經元在網絡中的誤差。求上一層的誤差，需要找出上一層中哪些節點與該輸出層連接，然后用誤差乘以節點的權值，求得每個節點的誤差，具體如圖所示：

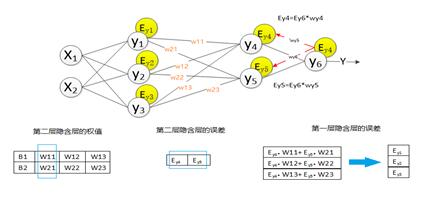
圖4-6全連接層中誤差的傳遞過程

1.2.2當前層為下采樣層，求上一層的誤差

在下采樣層中，根據采用的池化方法，把誤差傳入到上一層。下采樣層如果采用的是最大池化（max-pooling）的方法，則直接把誤差傳到上一層連接的節點中。果采用的是均值池化（meanpooling）的方法，誤差則是均勻的分布到上一層的網絡中。另外在下采樣層中，是不需要進行權值更新的，只需要正確的傳遞所有的誤差到上一層。

1.2.3當前層為卷積層，求上一層的誤差

卷積層中采用的是局部連接的方式，和全連接層的誤差傳遞方式不同，在卷積層中，誤差的傳遞也是依靠卷積核進行傳遞的。在誤差傳遞的過程，我們需要通過卷積核找到卷積層和上一層的連接節點。求卷積層的上一層的誤差的過程為：先對卷積層誤差進行一層全零填充，然后將卷積層進行一百八十度旋轉，再用旋轉后的卷積核卷積填充過程的誤差矩陣，并得到了上一層的誤差。如圖4-7為卷積層的誤差傳遞過程。圖右上方為卷積層的向前卷積過程，而右下方為卷積層的誤差傳遞過程。從圖中可以看出，誤差的卷積過程正好是沿著向前傳播的過程，將誤差傳到了上一層。

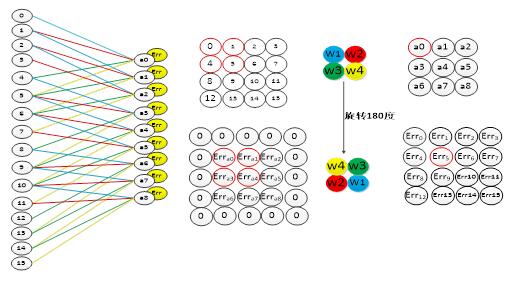
圖4-7卷積層的誤差傳遞過程

1.3卷積神經網絡的權值更新

1.3.1卷積層的權值更新

卷積層的誤差更新過程為：將誤差矩陣當做卷積核，卷積輸入的特征圖，并得到了權值的偏差矩陣，然后與原先的卷積核的權值相加，并得到了更新后的卷積核。如圖4-8，圖中可以看出，該卷積方式的權值連接正好和向前傳播中權值的連接是一致的。

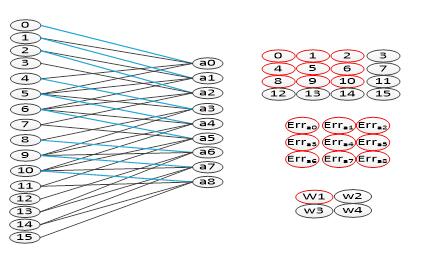
圖4-8卷積核的權值更新過程

1.3.2全連接層的權值更新過程

全連接層中的權值更新過程為：

1、求出權值的偏導數值：學習速率乘以激勵函數的倒數乘以輸入值；

2、原先的權值加上偏導值，得到新的權值矩陣。具體的過程如圖4-9所示（圖中的激活函數為Sigmoid函數）。

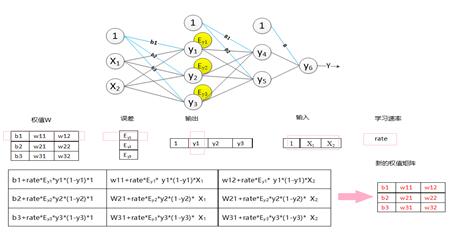
圖4-9全連接層的權值更新過程

責任編輯：YYX