線性回歸是人工智能機器學(xué)習(xí)里面最基礎(chǔ)的算法。
回歸概念
在介紹線性回歸之前先介紹下什么是回歸。回歸這個概念要追溯到19世紀(jì),最早是由高爾頓提出的,高爾頓是達(dá)爾文的表弟,他非常崇拜達(dá)爾文,他一生最著名的發(fā)現(xiàn)是父輩身高和字輩身高的關(guān)系。按照我們?nèi)粘=?jīng)驗,高個子的父輩子女也是高個子,矮個子的父輩子女也是矮個子,但大家并沒有發(fā)現(xiàn)另外一個規(guī)律,就是高個子的父輩子女平均身高要比父輩低,矮個子父輩身高比父輩高,這個叫做‘回歸’平庸,他認(rèn)為自然界有一種約束力,使得身高的分布不會向高矮兩個極端發(fā)展,而是趨于回到中心,所以稱為回歸。
在我們機器學(xué)習(xí)中的回歸其實就是從樣本數(shù)據(jù)中找到一個數(shù)學(xué)模型,找到事物的客觀存在的規(guī)律。
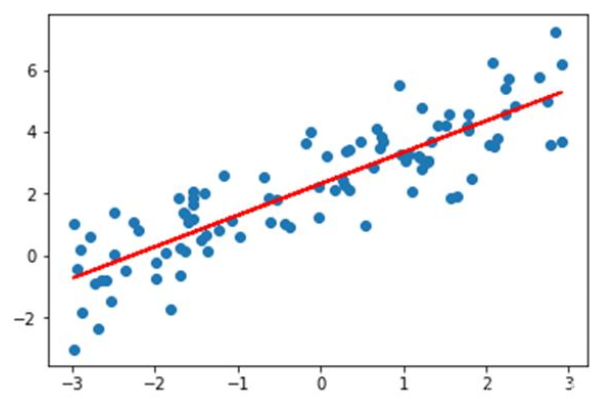
如上圖所示,藍(lán)色的點為樣本點,假設(shè)x軸是房屋面積,y軸是房屋價格,那線性回歸就是找到這樣一條紅色的直線,使得它對所有的樣本做出做好的擬合,也就是距離所有的樣本點平均距離最近,這樣當(dāng)有新的房屋面積需求時候,估計出來的房屋價格誤差就是最小的。
原理
我們上面看到了,要擬合一條直線符合樣本規(guī)律,則需要樣本到這條直線的平均距離最近。那怎么計算這個平均距離呢?
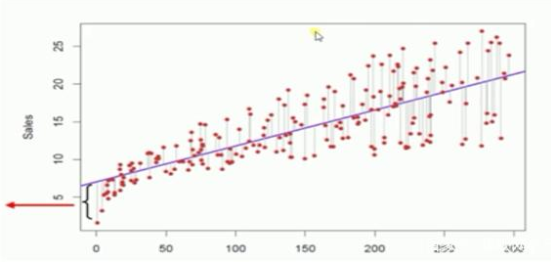
上圖所示,我們就計算每個樣本點到這條直線的‘垂直距離’,注意,是垂直距離,不是點到直線的距離,就是從樣本點向直線做一條平行于y軸的直線。大家看上圖就很快明白。
那這個距離怎么計算呢?這個就需要使用我們中學(xué)學(xué)過的幾何知識了。
二維坐標(biāo)下直線的方程為

我們就是求w1和w2 使得每個樣本點到這條直線的平均距離最短
假設(shè)樣本點的坐標(biāo)為(xi,yi)i=1-n,我們總共有n個樣本點。
那所有的樣本最短就要把所有點到直線的距離差計算出來,然后平方(消除負(fù)號,當(dāng)然求絕對值也可以,但計算更加繁瑣)
得到下面公式
這個公式被稱為線性回歸的損失函數(shù),參數(shù)是 w0 和w1,yi和xi為樣本數(shù)據(jù)。我們要求這個公式的最小值。
這個公式的最小值可以對w0 和w1 分別求導(dǎo)數(shù),得到下面公式
這個是一個二元一次方程可以解出來w0和w1的值。這就是最小二乘法的解法。
梯度下降法
上面的解法雖然能夠解出來w0和w1,但計算量很大,容易出錯。在工程上更多是使用梯度下降法進(jìn)行計算。
如上圖所示,梯度下降法就是從一個起始點出發(fā),不斷的試錯,就像閉眼睛下山一樣,每次都下降一小步,沿著下降最快的方向,也就是梯度最大的方向,不斷的這樣迭代,一直到下降的高度到達(dá)一個很小的值,就認(rèn)為到底谷底了。對凸函數(shù)來說,梯度下降法找的極值點就是全局極值點。
梯度下降法是一個迭代算法,主要是找到梯度下降的最大的方向,每次下降的步長是需要程序員自己設(shè)置的。如果設(shè)置得過大,會導(dǎo)致算法震蕩,如果過小則收斂速度太慢。如下圖的是步長過大跳過了極值點
梯度下降法的計算過程:
α是梯度下降法的步長,兩個式子分布是對w0和w1求偏導(dǎo)數(shù)。
-
人工智能
+關(guān)注
關(guān)注
1796文章
47683瀏覽量
240307 -
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8441瀏覽量
133088 -
線性回歸
+關(guān)注
關(guān)注
0文章
41瀏覽量
4316
發(fā)布評論請先 登錄
相關(guān)推薦
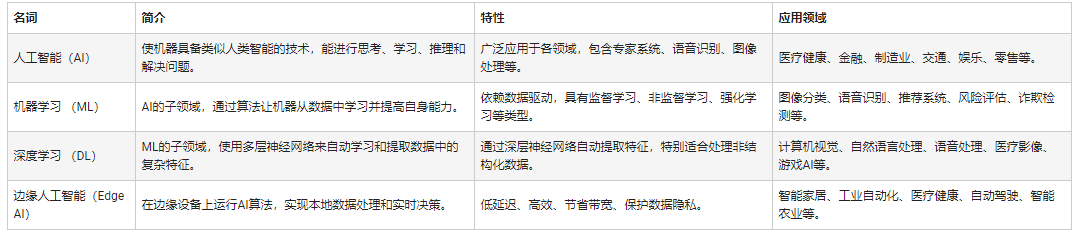
人工智能和機器學(xué)習(xí)以及Edge AI的概念與應(yīng)用
NPU與機器學(xué)習(xí)算法的關(guān)系
嵌入式和人工智能究竟是什么關(guān)系?
人工智能、機器學(xué)習(xí)和深度學(xué)習(xí)存在什么區(qū)別

《AI for Science:人工智能驅(qū)動科學(xué)創(chuàng)新》第6章人AI與能源科學(xué)讀后感
《AI for Science:人工智能驅(qū)動科學(xué)創(chuàng)新》第一章人工智能驅(qū)動的科學(xué)創(chuàng)新學(xué)習(xí)心得
FPGA在人工智能中的應(yīng)用有哪些?
人工智能、機器學(xué)習(xí)和深度學(xué)習(xí)是什么
機器學(xué)習(xí)算法原理詳解
5G智能物聯(lián)網(wǎng)課程之Aidlux下人工智能開發(fā)(SC171開發(fā)套件V2)
機器學(xué)習(xí)怎么進(jìn)入人工智能
5G智能物聯(lián)網(wǎng)課程之Aidlux下人工智能開發(fā)(SC171開發(fā)套件V1)
人工智能和機器學(xué)習(xí)的頂級開發(fā)板有哪些?





 線性回歸是人工智能機器學(xué)習(xí)里面最基礎(chǔ)的算法
線性回歸是人工智能機器學(xué)習(xí)里面最基礎(chǔ)的算法










評論