先前呢,我們在最受歡迎的十大機器學習算法-part1和最受歡迎的十大機器學習算法-part2兩篇文章中簡單介紹了十種機器學習算法,有的讀者反映看完還是云里霧里,所以,我會挑幾種難理解的算法詳細講解一下,今天我們介紹的是線性判別分析。
線性判別分析(Linear Discriminant Analysis)簡稱LDA,是分類算法中的一種。LDA通過對歷史數據進行投影,以保證投影后同一類別的數據盡量靠近,不同類別的數據盡量分開。并生成線性判別模型對新生成的數據進行分離和預測。
LDA投影矩陣
在維基百科中對投影的定義是:“投影是從向量空間映射到自身的一種線性變換,是日常生活中“平行投影”概念的形式化和一般化”。例如,在日常生活中,陽光會在大地上留下各種物體的影子。陽光將三維空間中的物體映射到影子的二維空間中,而影子隨著一天中太陽照射角度的變化也會發生變化。
如果你玩過游戲《Shadowmatic》就能理解LDA投影的過程。《Shadowmatic》是一款由TRIADA Studio開發的3D解謎游戲。游戲需要玩家在燈光下旋轉,扭動懸浮在空中的不明物體,并通過燈光的投影在墻上尋找不明物體的真面目。只要找對角度就能成功。如下面的游戲截圖中,不明物體在某個角度的投影是一只可愛的小兔子。
LDA投影矩陣與《Shadowmatic》相似。其中的不明物體是歷史數據樣本。我們需要通過“旋轉”和“扭動”這些歷史數據,找到正確的角度發現其中的模式。以下是銀行對企業貸款的樣本數據,其中包含了企業經營時間和拖延還款天數以及最終是否還款的數據。

我們把這些樣本數據生成散點圖,其中X軸是企業經營時間,Y軸是拖延還款天數,藍色三角表示未還款數據,紅色方框表示已還款數據。在散點圖中未還款和已還款數據相互交織,無法發現其中的模式。這就是游戲中的不明物體。

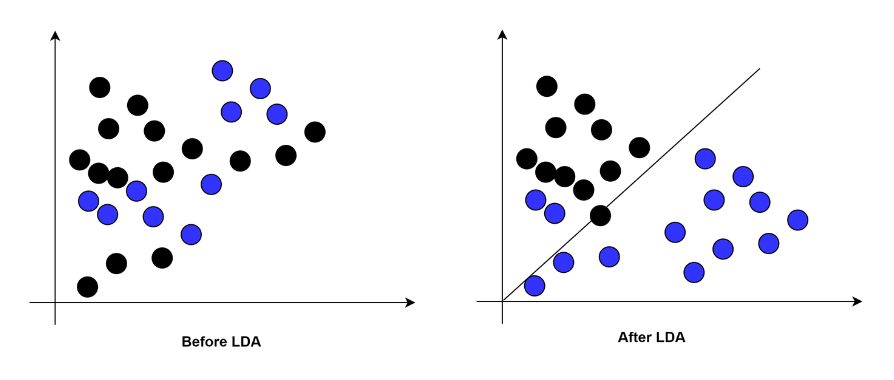
與游戲中不同的是我們無法“旋轉”和“扭動”樣本數據,而是要通過移動背景墻的位置來發現最終的“小兔子”。在下面的圖中,無論我們將樣本數據投影到X軸,還是Y軸,已還款和未還款的兩類數據都交織在一起,我們無法發現其中的模型。更無法對數據進行分類和預測。因為任何一個單獨的維度都無法判斷企業最終是否會還款。我們需要變換投影背景墻的位置來找到能將兩類數據分離的“角度”。

在LDA中這個投影背景墻是一個新的Y軸,角度是向量W。我們通過計算獲得向量W并生成新的Y軸,使兩個類別的樣本數據在新Y軸的投影中能最大程度的分離。計算向量W的方法是使用兩類數據的平均值差的平方除以兩類數據各自的方差之和。在這個公式中,我們希望分母越小越好,分子越大越好。換句話說就是兩類數據的均值相差的越大越好,這樣可以保證兩類數據間的分離程度。而同一類數據的方差越小越好,這樣可以保證每一類數據都不會太分散。這樣我們就可以找出一個W使J(W)的值最大。而這個最大值就是新的投影背景墻Y軸的方向。(這里需要通過拉格朗日來求W的最大值)

當歷史樣本數據被投影到新的Y軸背景墻時,可以看到數據與之前的情況不同,被明顯的分為了兩組。并且兩組數據間的交叉很少。這符合了LDA的預期,不同類別的數據間分離的越遠越好,同一類別的數據越集中越好。

到這里我們對兩類數據進行了分離,但這還不能實現對數據分類和預測。因此我們還需要找到一個點來區分這兩類數據。這個點就是線性辨別模型中。
LDA模式分類
線性辨別模型(Z=b1x1+b2x2)是一條直線方程,通過這條直線方程我們可以在散點圖中發現可以將兩組數據進行區分的數據點。并對新產生的數據進行分類和預測。如下圖所示,我們通過線性辨別模型獲得一條可以區分不同類別的直線。其中X1是企業經營時間,X2是拖延還款天數。而b1和b2是我們所要求的模型系數。

方差,協方差,協方差矩陣
在求線性辨別模型中的b1和b2時,需要用到協方差矩陣,因此我們先來簡單介紹與協方差有關的一些概念和計算方法。
均值
首先是均值,均值的計算很簡單。但要了解協方差和方差的概念,就必須先從均值開始。以下是均值的計算公式。均值表示一組數的集中程度。

方差
方差與均值正好相反,用來表示一組數的離散程度,也就是一組數中每一個數到均值的距離。由于均值通常是一組數的中心點,為了避免左右兩側的數據由于正負相互抵消無法準確的表示平均距離。我們先對距離取平方在進行匯總,匯總的結果就是方差的值。方差開平方就是標準差。

協方差
協方差是在方差的基礎上擴展得到的,從計算公式中就能看出來。協方差與方差有兩個最大的區別,第一個區別是方差是用來描述一組數的而協方差是用來描述兩組數的。第二個區別是方差用來描述一組數的離散程度,也就是離均值的距離,而協方差是用來描述兩組數直接的聯系的。
方差與協方差計算公式:


協方差是一種用來度量兩個隨機變量關系的統計量。
當cov(X, Y)>0時,表明 X與Y 正相關;
當cov(X, Y)<0時,表明X與Y負相關;
當cov(X, Y)=0時,表明X與Y不相關。
協方差矩陣
協方差只能處理兩組數(兩維)間的關系,當要計算的數據多于兩組(多維)時,就要用到協方差矩陣。協方差矩陣其實是分別計算了不同維度之間的協方差。通過下圖可以發現協方差矩陣是一個對稱的矩陣,對角線是各個維度上的方差。

計算線性辨別模型
在開始計算線性辨別模型之前,我們按企業是否還款將歷史數據分為已還款和未還款兩個類別。用以進行后面的計算。

計算均值,概覽及協方差矩陣
我們分別計算出已還款和未還款兩個類別中條目的數量,在整體樣本數據中出現的概率以及企業經營時間和拖延還款天數的均值。

按照前面介紹的協方差矩陣公式分別計算出兩個類別的協方差矩陣。從下圖中可以發現,協方差矩陣是一個對稱的矩陣,并且對角線上的兩個數字就是企業經營天數和拖延還款天數的方差值。

合并協方差矩陣
按照合并協方差的公式我們將兩個類別的協方差矩陣按出現的概率合并為一個協方差矩陣。以下是合并協方差的公式。

按照上面的公式,將每個類別的協方差矩陣乘以該類別的概率我們獲得了合并協方差矩陣。

逆協方差矩陣
最后我們對兩個類別的協方差矩陣求他的逆協方差矩陣。。

這是我們求得的合并協方差矩陣的逆矩陣。

計算線性辨別模型系數
求得逆協方差矩陣后,就可以通過兩個類別的均值差和逆協方差矩陣計算線性辨別模型的系數。下面分別給出了兩個類別的均值,逆協方差矩陣的對應表。


通過公式分別求出線性辨別模型的兩個系數b1和b2,以下是公式和計算步驟。

b1=0.0001(116.23-115.04)+0.0003(16.89-55.32)=-0.009696

b2=0.0003(116.23-115.04)+0.0037(16.89-55.32)=-0.143453
兩個系數分別為b1=-0.009696,b2=-0.143453。將系數值代入到模型中,就是我們所求的線性辨別模型。


責任編輯:gt
-
3D
+關注
關注
9文章
2910瀏覽量
107993 -
游戲
+關注
關注
2文章
750瀏覽量
26363 -
機器學習
+關注
關注
66文章
8438瀏覽量
133080
發布評論請先 登錄
相關推薦
【專輯精選】機器學習之算法教程與資料
基于核函數的Fisher判別分析算法在人耳識別中的應用
近鄰邊界Fisher判別分析
不相關判別分析算法在人臉識別中應用
核局部Fisher判別分析的行人重識別
基于逐步判別分析的血液氣味識別

python機器學習工具sklearn使用手冊的中文版免費下載

利用基于線性判別分析的多變量分析模型對豇豆種子進行分類
機器學習的基本流程和十大算法
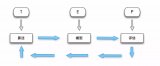




 十大機器學習算法中的線性判別分析的詳細介紹
十大機器學習算法中的線性判別分析的詳細介紹

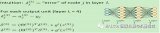










評論